浅谈WM算法

1.  WM（Wu-Manber）算法的简单理解：

 （1）WM算法需要的参数：

                ∑：字母集

                c： 字母集数目

                m：模式串集合中，字符串长度最小的模式串的长度

                B：字符块长度，是shift表的索引，一般取2或者3

                h：当前扫描过程中长度为B的模式串子串

                T：文本串

                N：文本串总长度

                P=｛P1, P2....Pk｝：模式串集合

                k：模式串的数目

                C：前缀长度（PREFIX表使用）

 （2）WM算法的时间复杂度：

         O（BN/kM），由此可以看出，WM使用于大规模的模式串集合且模式串集合中最小长度较大的场景！

 （3）WM算法的核心思想：

         WM算法是对BM算法的延伸继承，用BM算法的核心框架，用字符块来计算shift表（取代坏字符表）进行跳转，在进行匹配时，用hash和prefix计算前后缀的hash值来从众多可选的模式串中快速筛选出正确匹配的模式串。

 （4）WM算法的三张核心表：

          shift表：用于记录文本串向右移动的长度，即一张跳转表（ps：有点类似BM算法的坏字符表，不过BM是针对单字符，WM是针对字符块）。

          hash表：hash表记录了所有模式串后缀（长度为B）与模式串本身的映射关系。当shift[h]=0时，B与对应模式串P的映射关系，但是存在一对多的映射，因为模式串集合中存在相同后缀的模式串，所以hash表的value应该是一个链表的形式，存储多个模式串（ps：当shift[h]=0时，说明匹配到了某模式串，此时要用hash表查匹配到了哪个模式串P）

          prefix表：prefix记录了所有模式串前缀（长度为B）与模式串本身的映射关系。同hash表一样，B与对应模式串P的映射关系存在一对多，所以prefix表的value也是一个链表的形式，存储多个模式串。（ps：hash与prefix两个表取交集极大地缩小了需要匹配的次数）

 

2.  WM（Wu-Manber）算法的匹配过程：

    当B个字符构成的子串h在模式串集合中没有匹配，即shift[h]<0，则跳转的距离是：m-B+1（相对保守的策略）

    当B个字符构成的子串h在模式串集合中有匹配且非后缀，即shift[h]>0，则跳转的距离是：shift[h]（相对安全的滑动）

    当B个字符构成的子串h在模式串集合中且是后缀，即shift[h]=0，则查hash和prefix表确定匹配到了哪个模式串

 

3.  WM（Wu-Manber）算法的简单例子（来自joylnwang专栏-WM算法详解）：

  目标串target[1...10]=dcbacabcde，模式结合P={abcde,bcbde,abcabe}（ps：m=5，B=2，k=3，C=2），预处理后得到的三张表如下所示：

　　　　

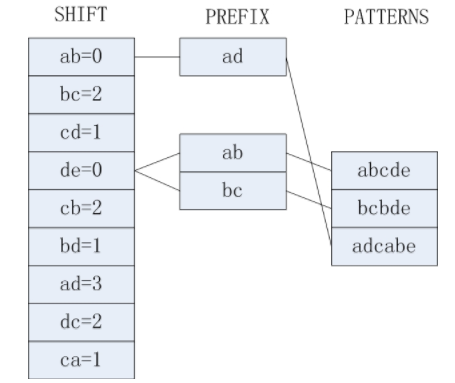
   WM算法的匹配过程是：

    （1）从i=5（因为m=5）开始执行算法，首先我们发现target[4...5] = ac（target[i-B+1](5-2+1)），SHIFT表中不存在ac，所以i = i+4 （shift表中没找到，则 i += m-B+1）

    （2）此时i=9，发现target[8...9]=cd，查SHIFT[cd]=1，所以i += SHIFT[cd]。

    （3）此时i=10，然后发现target[9...10]=de， 查SHIFT[de]=0，表明可能出现匹配到模式串的情况。

    （4）查HASH[de]有两个模式串abcde和bcbde；在target中取长度为C的从i-m+1开始的子串，即target[6...7] = ab，查PREFIX[ab] = abcde。此时确定模式串是abcde。

 

4.  WM（Wu-Manber）算法的程序实例：