Monte Carolo Method---Generating Random Variable
最近在阅读一本书Introducing Monte Carlo Methods with R,这本书主要的目的就是使用R这个语言来介绍蒙特卡洛方法,希望能借这个机会彻底弄懂蒙特卡洛法。
现在看到第二章,主要的内容就是如何使用均匀分布来生成所有其他我们想要的分布,其实类似的内容我已经在Pattern Recognition and Machine Learning中看到过的,
方法如下:
- Inverse Transform Method
- General Transformation Method
- Accept-Reject Method
Inverse Transform Method: 对于一个具有概率密度ƒ的分布来说,它的cdf函数F(X)是一个0~1区间的均匀分布,然后一个定理就是:对某个概率分布的cdf函数F求
逆,所获得的结果符合原来随机变量的概率密度。下面来定义一个cdf函数F(X)的求逆操作:
![]()
因此如果我们能获得显式的cdf函数,那么就可以从均匀分布获得这个cdf函数所对应的概率密度函数。
General Transformation Method: 有些概率分布之间存在一定的简单关系,比如n个a概率分布的相加,所获得结果符合概率密度b分布,这样我们就可以使用这种特性
来使用简单的概率分布获得复杂的概率分布。
Accept-Reject Method: 上面的方法都是有自己的局限的,对于Inverse Transform Method来说,并不是所有的概率分布的cdf都能显式表示成函数形式的。对于General
Transformation Method来说,有些非标准的概率分布不能用这种方法获得,但是Accept-Reject Method就可以克服以上方法的局限性,模拟任意概率分布(前提是存在
一个简单的概率分布g)。需要满足的条件包括以下几个:
- 当f(x)大于0的时候,g(x)也必须大于0
- 对于所有的x,{f(x)/g(x)} 小于等于 M 恒成立。
因此Accept-Reject方法如下,首先产生一个y,符合概率分布g,然后再产生一个u,属于0~1区间的均匀分布,如果满足如下关系,则接受y,否则重新开始。
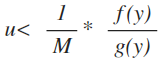
对于这个方法来说有以下几点需要注意:
- 这个方法需要ƒ和M,对于归一化常量则没有要求
- 这个方法不需要M非常的精确,可以稍微大一点,或者很多。但是问题是任意一个y被接受的概率是1/M,因此在可能的情况下,M越小越好。


