集体智慧编程笔记------推荐系统

第二章的内容主要是介绍推荐系统的基本原理。如果想要搭建一个推荐系统，最基本的组件就是相似性的判定，比如用户的相似性，物品的相似性。

从另一个方面来说，相似性可以很简单，也可以很复杂，取决于你所需要的效果，比如百度知道在一个问题的下面都会提供很多相似的问题，这个我觉得

也是相似性判定的一部分，恐怕就没有书里讲的那么容易，当然这两个东西所要处理的数据格式也是有很大的差别的，书中的数据都是非常简单的-浮点数

之类的，但是百度知道的数据是自然语句，难度不可能在一个数量级。

 书中介绍了两个方法，一个是判断两个用户（物品）的欧式距离，算法如下：首先找到两个用户共同评价的事物（比如电影），然后以每一部电影

作为一维，用户的对这个电影的评分是相应维的坐标值，那么一个用户就可以被刻画成n维空间中的一个点，两个用户相似性的判定就可以通过判断代表

用户的两点之间的欧式距离来决定。这个相似性判定方法存在问题，如果一个用户倾向于给出较高的分值，而另一个则倾向于较低的分值，那么着两个用户

的相似性就因此而被低估。

另一个判定相似性的方法是判断两个用户打分的一致性，虽然两个用户评分的严厉程度不同，但是如果趋势相同，那么这两个用户就较为相似。具体

方法就是计算打分的相关性，公式如下：。这个变量的取值介于-1和+1之间，不过为0，表示

两个变量并不是线性相关的，-1则表示负线性相关，+1表示正线性相关。如果用在用户推荐系统中，那么-1表示很厌恶，+1表示兴趣相同。对于如何在样本

计算相关性，可以使用如下的公式：

　　　　　　　　　　　　　　　　　　 

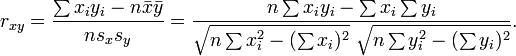
如果和书中代码相比较，可以发现，书中就是实现了这个公式 ，即：计算样本上的相关性。更详细的信息可见http://en.wikipedia.org/wiki/Pearson_product-moment_correlation_coefficient。

　　　以上面两种方法为基点，书中给出几个简单的应用。

　　1.基于用户的数据，给出和用户相近的用户列表，这个就是简单的计算两个用户的相似性，然后排序。

　　2. 基于用户的数据，给用户推荐商品。这个就非常有趣，比第一个的处理更多，对于一个商品，不同的用户必然有不同的评价,而一个用户跟不同用户具有不同

的相似性，那么这个用户对这个商品的可能评价可由所有这些评价过的分数来取得，加权计算，即用相似性乘以评价分数，相加，然后除以相似性的总和，即获得

用户的可能评分。

　　以上整个的做法，有一个专门的称呼，那就是collaborative filtering，其实有两种不同的类型，一种称之为 user-based collaborative filtering，另一种就

是item-based collaborative filtering。前面介绍的就是used-based方法，item-based方法首先是离线或在独立的地方首先计算所有物品之间的相似性，当需要

向用户推荐时，可以立即使用已经的物品相似性数据库向用户做出推荐。used-based方法就是想计算用户相似性，然后再推荐物品。

　　那么两个方法的区别是什么呢？其实主要的方法都是相似的，一个方法是首先计算好需要的数据（item-based），在需要的时候使用，然后当数据发生了很大的改变的时候再重新改变，好处在于节省了时间。使用的范围是数据稀疏的时刻，就是不同用户评价的物品的交集非常小，如果不是这样，那么使用used-based和item-based区别不是很大。