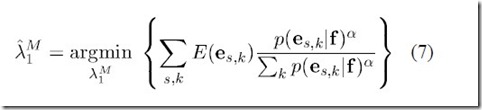机器翻译中的参数调整---MERT方法
机器翻译的大牛Och在2003提出的方法,用于统计机器翻译中对数线性模型参数的调整,这几天读了这篇论文,也算是有了点了解。写篇文章,要不然就忘了,哈哈。
Och在文章中提出在之前的参数调整方法中,参数的确定和最终的翻译质量并没有什么紧密的联系,比如在统计机器翻译的对数线性模型中feature的权重需要调整,使用的
准则就是如下的公式:
这个公式的意思是如果一个参数λ使得对于训练集中的所有据对取得最大值,那就是最好的参数。
但是大神觉得这没什么道理,需要一种方法来讲最终的评价结果和调参结合起来。于是最小错误率训练法就呼之欲出了。不同于上述的使用feature值来调整参数,MERT方使用的是
假设中存在的一个函数E,来统计一个翻译的结果和标准翻译相比所存在的错误的个数,E(e,r)的意思就是对一个句子f的翻译e和标准翻译r相比存在的错误的个数。对一个句子集合F,统
计每个句子f的翻译错误,使得翻译错误总数最小的参数才是最好的参数,于是有了下面的准则函数:
假设我们有一个待翻译的外文集合,这个集合中共有S个待翻译的句子f1,f2,f3…fs, 每个句子fi都有一个set of K candidate translation Ci,Ci={ei,1 , ei,2 ,…, ei,k },计算错误个数的时
候并不是对Ci中的每个句子都统计翻译错误,而是对其中可能性最大的翻译统计翻译错误,这个就是公式(6)的解释:在一个参数λ的作用下,得分最高的翻译e作为Ci中的代表,去统计
e和标准翻译r的错误率。公式(5)就是对这个集合S中的每一个外文句子f进行这样的统计得到中的错误率,使得总的错误个数最小的参数就是最好的参数。但是这个公式是不平滑的,下
面还有一个平滑的版本:
相对于没有平滑的版本来说,改进的地方在于局部极小值减少了,如果使用未经平滑的版本,那么存在太多的局部最小值,使得寻找全局最小值存在极大的困难。
可以看到这个准则将直接将错误用于参数的调整之中,根据实验这种做法提高了系统的翻译质量,同时Och大牛针对未经平滑的最小错误准则函数提出了一个优化的方法,用于寻找较
优的参数。这种优化方法是基于Powell search的方法。
Powell search方法来寻找有n维的参数向量时,一次只能够优化一维向量,优化n维参数则需要n次迭代来完成。Och提出的方法也是基于同样的原理,优化时只能针对某一维向量进
行,其余维数的向量必须固定,具体的方法如下:
假如整个n维参数向量中只有一维能够变化,其余维数固定,一个待选翻译(candidate translation)的得分在对数线性模型下成为kx+b的形式,x就是可以变化的那一维参数,其余
参数固定,其相应的得分直接退化成了常数b,对于有k个待选翻译的外文f,就有对应的k条直线。根据Eqn(6),需要从k个翻译中挑选出得分最高的句子,然后统计错误个数。当我们将
得分表示成线性函数时,被挑中的翻译就是对应于同一个x,得分最高的那个翻译,选出这个翻译后,然后再去统计错误个数。其实我们也可以这样做:当将翻译得分转化成线性函数时直
接使用函数E来统计错误的个数,这个时候线性函数的形式转化为t(e,f)+r*m(e,f),t(e,f)和m(e,f)相对于r来说都是参数,这个函数的结果就是此时取值的错误个数,那么挑选最优的翻译就
非常明显:值最小的。挑选函数的形式就是f=argmin(t(e,f)+r*m(e,f)),e是k个翻译之一,这个函数明显是分段的,所以存在一系列的间断点r1,r2 ,r3 ,…,rk 。对于具有n个
句子的外文语料库,存在n个这样的分段函数,每个函数都有一系列的间断点。为了取得整个语料库上表现的得分的最优,将所有这些n个函数叠加,当在某个区间内取值为最小的时候,
这个时候对应的参数就是最优的参数。对n维的每一维都必须进行这样的过程以确定参数。不同于powell 搜索,这个算法可以确保获得最优值,原理我就不知道了…
以上所述就是Och在03年发表的论文minimum error rate training in statistical machine translation,只是描述清楚而已,没啥理解,汗啊