带你轻而易举的学习python——八皇后问题
首先我们来看一下这个著名的八皇后问题
八皇后问题:在8×8格的国际象棋上摆放八个皇后,使其不能互相攻击,即任意两个皇后都不能处于同一行、同一列或同一斜线上,问有多少种摆法。
在这个问题提出之后人们又将它扩展到了n×n格的棋盘摆放n个皇后有多少种摆法
其实这是只有在8×8出现这种问题吗?那显然不是嘛,只是发明国际象棋那哥们把棋盘设计成了8×8,再配合上下棋人的跳跃性思维于是乎产生了八皇后问题。如果当时把棋盘设计成了4×4,那现在可能就会叫4皇后问题了。
无论是几个皇后 道理都是一样的嘛。对吧
今天我们就以4×4的棋盘为例来解答这个问题
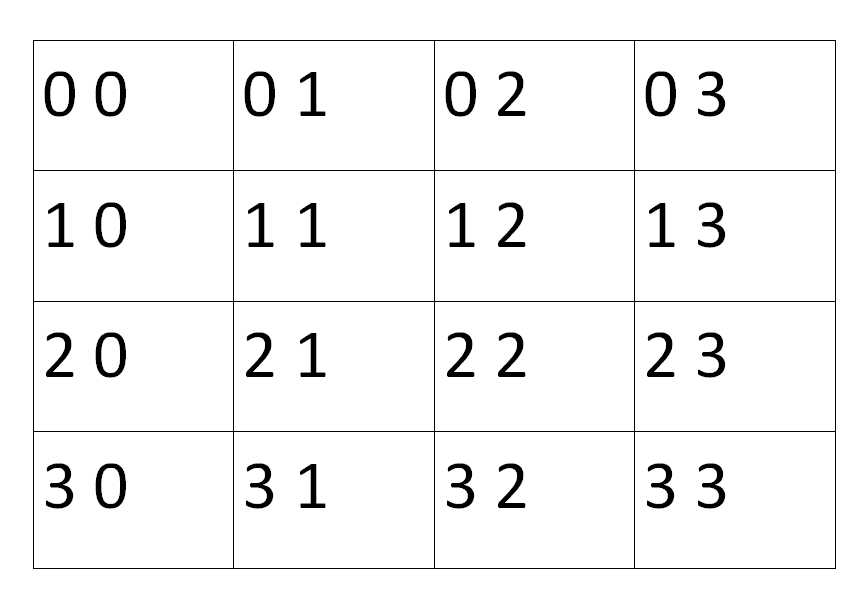
我们看上边的4×4的小棋盘,也就是八皇后棋盘的儿子哈哈
在这里对棋盘中的所有格子都进行了标号,这标号可不是我随心所欲标出来的,这是根据我们众所周知的二维数组的行列标号所标出来的。每个小方格里都有两位数字,第一位表示该格子所在的行标号(从0开始),第二位顺其自然也就是列标号了。
仔细看这张图的数字,你发现了什么规律吗?
我们把行标号定义为x,列标号定义为y。我们可以用坐标的形式来表示每一个小方格。这是我们回想初高中所学过的函数知识啦 当然这个函数不是我们编程语言中的函数哈
我们在二维坐标系中,可以根据一条直线上的两个点求得该直线的斜率,即:k(斜率)=(y2-y1)/(x2-x1) (x1,y1)与(x2,y2)为直线上的任意两点
这里有特殊的两条直线:y=x(斜率为1) 与 y=-x(斜率为-1) 即k=1 所以:|y2-y1| = |x2-x1|
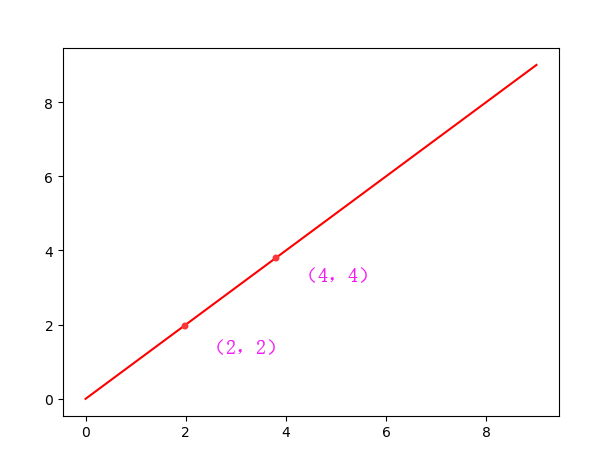
看上边这个图,回忆我们初中的数学知识是不是就一目了然啦
下边是用python实现画上图的代码,感兴趣的朋友可以回去试一试哈,很神奇的
# -*- coding: utf-8 -*-
import numpy #调用numpy的包 import matplotlib.pyplot as plt #调用matplotlib包中的pyplot算法
n = numpy.arange(10)
plt.plot(n,n,color="r") #用红色的线条
plt.show()
解决皇后的问题呢,在这说了这么多斜率干嘛呀?跑题了吧 不但没有 而且二者有很大的联系 斜率为1不就是与水平面夹角45°嘛 斜率为-1不就是与水平面夹角135°嘛 上边的图中任意斜线上的方格连成一条线正好是45°或135°。不信我们随便取两个。
我们在上边的图中任意找两个在任意斜线上的方格 比如我找(1,3)和(3,1) 连线呈45°角,可见|1-3|=|3-1| 我在找(3,2)和(1,0)同样也满足 也就是说处于同一斜线上的两个方格同时也会满足|y2-y1| = |x2-x1|。
有的朋友可能已经忘了什么斜率这些概念了 都没有关系,你只需要记住在同一斜线的两个方格存在这种列表号差的绝对值与行标号差的绝对值相等即可。
好了,该说的都说了,上代码吧
# -*- coding: utf-8 -*- num = 0 # 八皇后摆放函数 第一个参数为一维数组 数组的每个下标代表每个皇后所摆放的行号,对应的数组中的数表示该皇后所摆放的列号 def eight_queen(arr,finish_line=0): if finish_line == len(arr): #如果放置皇后成功的行数与数组中的元素个数一致(即棋盘的行数)则认为完成了一种摆法 global num #将上边定义的num定义为全局变量 这样才能在后边对其进行自加操作 num+=1 print("第%s种摆法:" % num) for i in range(8): print((i,arr[i])) return 0 for stand in range(len(arr)): #对整个列进行扫描,将列标的标号赋值给数组中对应的元素 arr[finish_line] = stand flag = True for line in range(finish_line): #判断前几行对应的这一列有没有皇后 或者当前列是否与之前的皇后处在同一斜线上 两者在之一则列加一(向右边换一列再试试) if arr[line] == stand or abs(arr[line]-stand) == finish_line-line: flag = False if flag==True: eight_queen(arr,finish_line+1) if __name__ == '__main__': #主函数 eight_queen([0]*8) if num != 0: print("一共有%s种摆法" % num) else: print("无解")
代码解析:运行代码,首先执行if __name__ == '__main__':下边的 eight_queen([0]*8)
找到def eight_queen(arr,finish_line=0):第一次执行时:finish_line=0,表示我先在要往棋盘的第0行放置皇后了 进行if finish_line == len(arr):
的条件判断,数组的长度为8 而finish_line为0 显然不成立 跳过if分支 刚刚只说我要往第0行放皇后 那么具体放到第一行的那个位置呢? 别着急 我们进入到下边的for循环中(这里stand变量表示列):第一次进入for循环中 stand=0(第0列),此时:arr[0]=0;
也就是说第一个皇后等待放在第0行第0列的位置。在这里定义一个flag标志位,在后边用来判断刚刚待等待放置的皇后能否在第0行第0列的位置放置。
接下来走到了下边的for循环 line=0 而 finish_line也为0 所以不会进入循环 直接执行if语句判断标志位 我们刚刚定义的就是True 所以当然成立了。这时成功的调取了 eight_queen(arr,finish_line+1) 表示我第一个皇后放置成功了,我需要往下一行(第1行)放皇后了
这是第二次调用该函数 此时 finish_line=1 要往第1行放皇后了 大部分执行与第一次完全一致 唯一不同的就是这时需要进行刚刚没有执行的for循环了
我要往第1行的第0列放置皇后了 现在需要判断在第1行之前的0列上是否有皇后 怎么判断呢? 我刚刚把被占用列已经放到的arr这个数组中了啊 只需要判断我这次往数组中放的列原来在数组中有没有不就行了嘛
于是我们判断arr[0]==stand吗? 我们已知arr[0]为0(第0行第0列有皇后) 所以第1行第0列不能再有皇后了 继续执行循环体 判断第1行第1列能放皇后吗?arr[0]==stand显然不成立 而第1行第1列与第0行第0列正好处于同一斜线 即|1-0|=1-0 所以这个格子也不能放皇后。
继续执行循环体 判断第1行第2列能放皇后吗? 会发现if的两个条件都不满足 那当然可以放了 于是第二个皇后有着落啦 往后的每一个皇后都是这样去循环判断是否可以放置的。
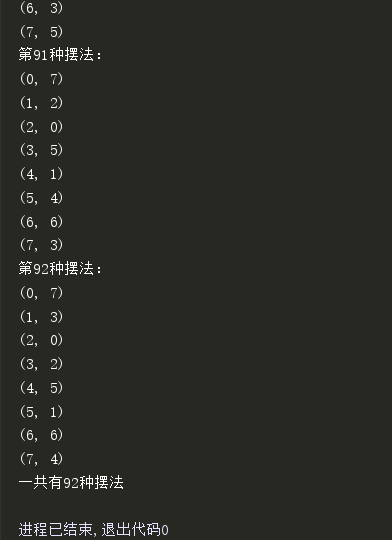
程序运行结果部分截图,可见输出都是皇后摆放位置的坐标。当然如果你想解决n皇后的问题,直接把eight_queen([0]*8)中的8改成你心中的n就Ok啦。
再看下边这个程序:
# -*- coding: utf-8 -*-
arr2 =[[0, 0, 0, 0, 0, 0, 0, 0], #用二维数组来模拟那个8*8的棋盘(low到爆的办法) [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0]] num = 0 def eight_queen(arr,finish_line=0): if finish_line == len(arr): #如果放置皇后成功的行数与数组中的元素个数一致(即棋盘的行数)则认为完成了一种摆法 for x in range(len(arr2)): for y in range(len(arr2)): arr2[x][y]=0 global num #将上边定义的num定义为全局变量 这样才能在后边对其进行自加操作 num+=1 print("第%s种摆法:" % num) for i in range(8): for x in range(len(arr2)): for y in range(len(arr2)): if i == x and arr[i]==y: arr2[x][y] = “皇” print(arr2) return 0 for stand in range(len(arr)): #对整个列进行扫描,将列标的标号赋值给数组中对应的元素 arr[finish_line] = stand flag = True for line in range(finish_line): if arr[line] == stand or abs(arr[line]-stand) == finish_line-line: flag = False if flag==True: eight_queen(arr,finish_line+1) if __name__ == '__main__': eight_queen([None]*8) if num != 0: print("一共有%s种摆法" % num) else: print("无解")
看上去比刚刚好点啦,但是还是很别扭,接下来我们引用科学计算的内容numpy来转这个数组
# -*- coding: utf-8 -*- import numpy #引用numpy包(引之前需要安装numpy解释器) arr2 =[[0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0], [0, 0, 0, 0, 0, 0, 0, 0]] num = 0 def eight_queen(arr,finish_line=0): if finish_line == len(arr): #如果放置皇后成功的行数与数组中的元素个数一致(即棋盘的行数)则认为完成了一种摆法 for x in range(len(arr2)): for y in range(len(arr2)): arr2[x][y]=0 global num #将上边定义的num定义为全局变量 这样才能在后边对其进行自加操作 num+=1 print("第%s种摆法:" % num) for i in range(8): for x in range(len(arr2)): for y in range(len(arr2)): if i == x and arr[i]==y: arr2[x][y] = "皇" arr3 = numpy.array(arr2) #将二维数组转化成array格式(就是一种格式而已,转完了就是好看) print(arr3) return 0 for stand in range(len(arr)): #对整个列进行扫描,将列标的标号赋值给数组中对应的元素 arr[finish_line] = stand flag = True for line in range(finish_line): if arr[line] == stand or abs(arr[line]-stand) == finish_line-line: flag = False if flag==True: eight_queen(arr,finish_line+1) if __name__ == '__main__': eight_queen([None]*8) if num != 0: print("一共有%s种摆法" % num) else: print("无解")
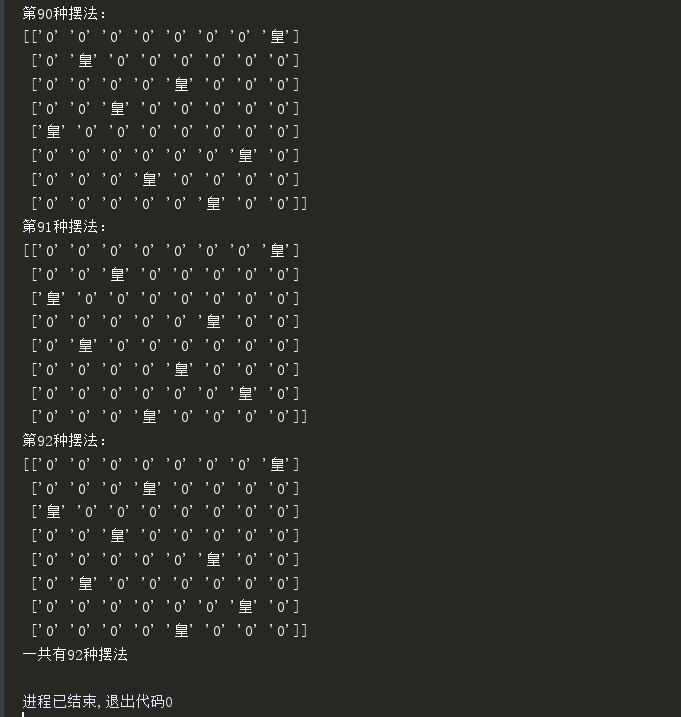 。
。
这回就好看多啦是吧。
第一次写,望读者有意见多多指出。




