BUAA OO 2022 第一单元总结

前言

本文主要包括对第一次作业和第二次作业的设计思路、代码度量分析.以及三次作业中发现的Bug
笔者在三次作业的迭代中并没有重构过，而且第二次作业已经完全实现了第三次作业的功能。故只对第一次和第二次的代码进行具体分析.
如果用一句话概括本人写第一单元作业的核心思路,就是:"先以Factor为中心解析表达式,再以Expression为中心合并表达式".

1. 第一次作业

1.1 设计思路

解析部分:第一次作业虽然数据限制的很死，只允许有一层括号，但是为了后续能顺利的进行迭代，所以采取了可扩展性更强的递归下降的方式去解析。接下来将以最终版的Parser为例介绍解析的过程.其中,黑色的线表示函数的调用顺序,蓝色的线表示调用特殊操作,红色的线表示递归调用.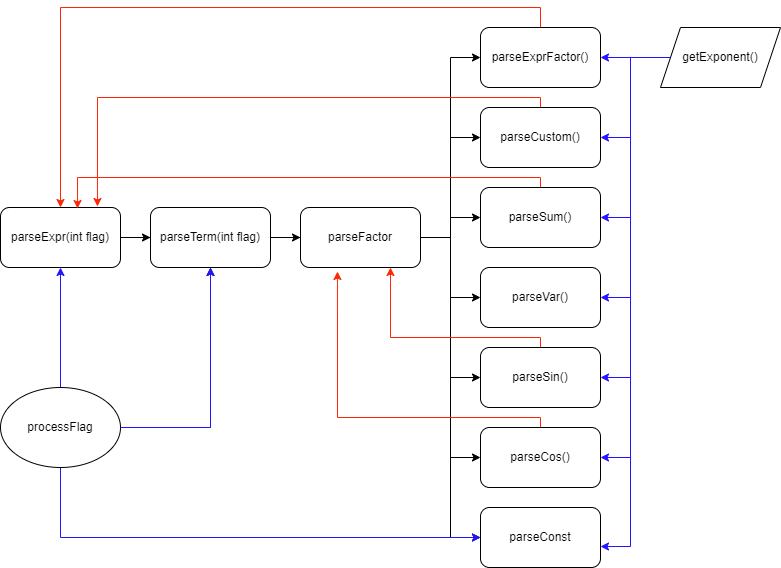
- 关于正负号的处理: 据我了解,有一些同学采取了预处理的方式去替换掉"多余的"正负号,我认为这种操作方式并不合理. 因为表达式中所有的正负号都有自己独特的意义,并没有多余. 如图所示,我在处理表达式,项,常数之前,都进行了处理符号的操作. 这种方法其实是完全按照形式化表述去解析, 从第一次作业开始到最后都没有产生过错误.
- 其余部分的解析操作, 大多与traning中给出的代码相同.
建树部分: 建树部分使用了HashSet作为容器, Expr中包含一堆Term,Term中又包含一堆Factor,从而建立起一个表达式树.
数据计算部分: 数据计算和建立表达式树采取了不同的数据结构,因为Expr-Term-Factor的结构缺乏一种统一性,不便于合并化简计算.考虑到第一次作业中只有常数,x,和幂,因此我采用了HashMap<Integer, Variable> vars去统一各项,最终实现合并同类项化简.

1.2 代码度量分析

类图: 将HashMap<Integer, Variable>简写为H. 为了拓展程序,第一次作业中有些方法写出来了但是并未使用过,不在类图中显现.cal()方法即可以把层次结构转化为相应的统一HashMap<Integer,Vatiable>

如下表,可见Parser.parseFactor(int)方法复杂度较高, 因为因子的解析是第一次作业的核心

Method	CogC	ev(G)	iv(G)	v(G)
Lexer.Lexer(String)	0	1	1	1
Lexer.getCurToken()	0	1	1	1
Lexer.getNumber()	5	2	4	6
Lexer.next()	3	2	3	4
Lexer.peek()	0	1	1	1
Lexer.setCurToken(String)	0	1	1	1
MainClass.getNumReverse(StringBuilder, int)	2	1	3	3
MainClass.main(String[])	16	1	8	9
MainClass.preStrRefine(String)	13	1	6	6
Parser.Parser(Lexer)	0	1	1	1
Parser.parseExpr(int)	6	1	5	6
Parser.parseFactor(int)	39	8	16	16
Parser.parseTerm(int)	3	1	4	4
experssion.Expr.Expr()	0	1	1	1
experssion.Expr.add(Factor)	0	1	1	1
experssion.Expr.addHashMap(HashMap<Integer, Variable>, HashMap<Integer, Variable>)	4	1	3	3
experssion.Expr.addTerm(Term)	0	1	1	1
experssion.Expr.cal()	0	1	1	1
experssion.Expr.calFlag(int)	0	1	1	1
experssion.Expr.mulHashMap(HashMap<Integer, Variable>, HashMap<Integer, Variable>)	7	1	4	4
experssion.Expr.pow(int)	1	1	2	2
experssion.Expr.toString()	3	1	3	3
experssion.Term.Term()	0	1	1	1
experssion.Term.addFactor(Factor)	0	1	1	1
experssion.Term.cal()	0	1	1	1
experssion.Term.mulHashMap(HashMap<Integer, Variable>, HashMap<Integer, Variable>)	7	1	4	4
experssion.Term.toString()	3	1	3	3
experssion.Variable.Variable(BigInteger, int)	0	1	1	1
experssion.Variable.add(Factor)	0	1	1	1
experssion.Variable.addVar(Variable, Variable)	1	2	2	2
experssion.Variable.cal()	0	1	1	1
experssion.Variable.calFlag(int)	1	1	2	2
experssion.Variable.getCoe()	0	1	1	1
experssion.Variable.getExpo()	0	1	1	1
experssion.Variable.isNegative()	2	2	1	2
experssion.Variable.pow(int)	0	1	1	1
experssion.Variable.setCoe(BigInteger)	0	1	1	1
experssion.Variable.setExpo(int)	0	1	1	1
experssion.Variable.toString()	13	9	5	9
Average	3.31	1.49	2.54	2.79

class	OCavg	OCmax	WMC
experssion.Expr	1.89	4.0	17.0
experssion.Term	2.0	4.0	10.0
experssion.Variable	1.92	9.0	23.0
Lexer	2.0	4.0	12.0
MainClass	5.0	8.0	15.0
Parser	6.5	16.0	26.0
Total			103.0
Average	2.64	7.50	17.17

1.3 Bug分析

第一次作业的难度较小,在强测和互测中均没有出现bug.
发现的他人bug为:将-1无脑转化为-出错

2. 第二次作业

2.1 设计思路

自定义函数: 由于自定义函数都是简单函数,与其把它当作函数,不如把他当作C中的函数宏去解析.
- 自定义函数类: 将函数定义式分为LHS和RHS两段, LHS中提取变长数组ArrayList<String> Parameters,以及String funName. 核心是方法String calFuntion(String str),将str中提取相应的参数,代换掉RHS中的形式参数,从而得到一个新的字符串.
- sum函数类: 继承自定义函数,重写了String calFunction(String str)方法.
- 函数调用实现:如前边所说,我们通过calfunction方法可以得到完成字符串带入的新字符串,而后,我们重新递归调用Lexer和Parser去解析这个表达式(字符串), 最终同样可以返回一个Expr.这种方法有一下几点优势:
  - 重复利用写好的解析函数的类,天然支持函数嵌套.
  - 同时具有暴力替换的简洁性和构建单独模型的可扩展性.
建立表达式树: 基本和第二次作业一样,将新的三角函数作为一种Factor,同时分离了Variable和Const
数据合并部分: 如前言中所说, 数据合并部分我采用以Expr为核心的化简方式,所以要构建出一种数据结构去统一表达式中的不同层次. 因此,将作业1中的单层的HashMap<BigInteger,Variable>转化为了讨论区中大佬提出的HashMap<HashMap<String,BigInteger>,BigInteger>. 在每个层次结构中都实现cal()方法,将其转化为统一结构.

2.2 代码度量分析

类图展示
- 自定义函数与求和函数
- 层次结构如图所示:

如下表,可见几个特别复杂的方法分别出现在: 1.工具类Operation,其中写了两个多项式相乘,相加,乘方等等方法.2. Expr的unpack()方法. 这个其实是第三次作业中加入的,在很多地方都有调用,目的是看看能否把这个表达式"降级"为单个因子. 3. CustomFun.getPara(String)这个方法用于解析括号中的内容,获取"实参",由于第三次作业中加入函数嵌套,这里写的可能稍有复杂.

Method	CogC	ev(G)	iv(G)3.0	v(G)3.0
parse.Parser.processFlag(int)	2.0	1.0
parse.Parser.parseVar()	0.0	1.0	1.0	1.0
parse.Parser.parseTerm(int)	2.0	1.0	3.0	3.0
parse.Parser.parseSum()	7.0	5.0	5.0	5.0
parse.Parser.parseSin()	0.0	1.0	1.0	1.0
parse.Parser.Parser(Lexer, ArrayList)	1.0	1.0	2.0	2.0
parse.Parser.parseFactor()	8.0	1.0	9.0	9.0
parse.Parser.parseExprFactor()	1.0	1.0	2.0	2.0
parse.Parser.parseExpr(int, int)	2.0	1.0	3.0	3.0
parse.Parser.parseExpr(int)	2.0	1.0	3.0	3.0
parse.Parser.parseCustom(String)	10.0	7.0	6.0	7.0
parse.Parser.parseCos()	0.0	1.0	1.0	1.0
parse.Parser.getExp()	3.0	2.0	3.0	3.0
parse.Lexer.toString()	0.0	1.0	1.0	1.0
parse.Lexer.peek()	0.0	1.0	1.0	1.0
parse.Lexer.next()	4.0	2.0	4.0	5.0
parse.Lexer.Lexer(String)	0.0	1.0	1.0	1.0
parse.Lexer.isEnd()	2.0	2.0	1.0	2.0
parse.Lexer.getWord()	2.0	1.0	3.0	3.0
parse.Lexer.getNumber()	5.0	2.0	4.0	6.0
MainClass.main(String[])	1.0	1.0	2.0	2.0
function.SumFun.toString()	0.0	1.0	1.0	1.0
function.SumFun.SumFun()	0.0	1.0	1.0	1.0
function.SumFun.getFunName()	0.0	1.0	1.0	1.0
function.SumFun.callFunction(String)	8.0	3.0	4.0	5.0
function.CustomFun.toString()	0.0	1.0	1.0	1.0
function.CustomFun.isNumber(String)	3.0	3.0	2.0	3.0
function.CustomFun.getPara(String)	24.0	8.0	11.0	11.0
function.CustomFun.getFunName()	0.0	1.0	1.0	1.0
function.CustomFun.CustomFun(String)	1.0	1.0	2.0	2.0
function.CustomFun.CustomFun(int)	0.0	1.0	1.0	1.0
function.CustomFun.CustomFun()	0.0	1.0	1.0	1.0
function.CustomFun.callFunction(String)	12.0	1.0	7.0	7.0
experssion.Term.toString()	25.0	2.0	9.0	10.0
experssion.Term.Term()	0.0	1.0	1.0	1.0
experssion.Term.simplify()	2.0	1.0	2.0	2.0
experssion.Term.printTerm(HashMap)	11.0	1.0	4.0	4.0
experssion.Term.getFactors()	0.0	1.0	1.0	1.0
experssion.Term.cal()	0.0	1.0	1.0	1.0
experssion.Term.addFactor(Factor)	0.0	1.0	1.0	1.0
experssion.Operation.mulPoly2(HashMap, BigInteger>, HashMap, BigInteger>)	3.0	1.0	3.0	3.0
experssion.Operation.mulInner(HashMap, HashMap, boolean)	6.0	1.0	5.0	5.0
experssion.Operation.keyToMerge(HashMap)	7.0	1.0	8.0	8.0
experssion.Operation.addPoly2(HashMap, BigInteger>, HashMap, BigInteger>)	22.0	1.0	9.0	9.0
experssion.factor.Variable.Variable(BigInteger)	0.0	1.0	1.0	1.0
experssion.factor.Variable.toString()	3.0	3.0	2.0	3.0
experssion.factor.Variable.getExpo()	0.0	1.0	1.0	1.0
experssion.factor.Variable.cal()	0.0	1.0	1.0	1.0
experssion.factor.Sin.toString()	7.0	5.0	5.0	5.0
experssion.factor.Sin.Sin(BigInteger, Factor)	2.0	1.0	2.0	2.0
experssion.factor.Sin.getType()	3.0	3.0	2.0	3.0
experssion.factor.Sin.getExpo()	0.0	1.0	1.0	1.0
experssion.factor.Sin.cal()	15.0	4.0	7.0	9.0
experssion.factor.Cos.toString()	7.0	5.0	5.0	5.0
experssion.factor.Cos.getType()	3.0	3.0	2.0	3.0
experssion.factor.Cos.getExpo()	0.0	1.0	1.0	1.0
experssion.factor.Cos.Cos(BigInteger, Factor)	2.0	1.0	2.0	2.0
experssion.factor.Cos.cal()	7.0	3.0	5.0	6.0
experssion.factor.Const.toString()	0.0	1.0	1.0	1.0
experssion.factor.Const.getNum()	0.0	1.0	1.0	1.0
experssion.factor.Const.Const(BigInteger)	0.0	1.0	1.0	1.0
experssion.factor.Const.calFlag(int)	1.0	1.0	2.0	2.0
experssion.factor.Const.cal()	0.0	1.0	1.0	1.0
experssion.Expr.unpack()	46.0	12.0	20.0	20.0
experssion.Expr.toString()	25.0	2.0	9.0	10.0
experssion.Expr.toFactorString()	25.0	3.0	9.0	10.0
experssion.Expr.simplify()	2.0	1.0	2.0	2.0
experssion.Expr.setExpo(BigInteger)	2.0	1.0	3.0	3.0
experssion.Expr.printTerm(HashMap)	11.0	1.0	4.0	4.0
experssion.Expr.Expr(int)	0.0	1.0	1.0	1.0
experssion.Expr.Expr()	0.0	1.0	1.0	1.0
experssion.Expr.cal()	0.0	1.0	1.0	1.0
experssion.Expr.addTerm(Term)	2.0	1.0	2.0	2.0
Total	339.0	132.0	231.0	247.0
Average	4.64	1.81	3.16	3.38

class	OCavg	OCmax	WMC
parse.Parser	3.0	7.0	39.0
parse.Lexer	2.2857142857142856	5.0	16.0
MainClass	2.0	2.0	2.0
function.SumFun	2.0	5.0	8.0
function.CustomFun	2.875	8.0	23.0
experssion.Term	2.857142857142857	10.0	20.0
experssion.Operation	5.0	9.0	20.0
experssion.factor.Variable	1.5	3.0	6.0
experssion.factor.Sin	4.0	9.0	20.0
experssion.factor.Cos	3.4	6.0	17.0
experssion.factor.Const	1.2	2.0	6.0
experssion.Expr	4.6	12.0	46.0
Total			223.0
Average	3.0547945205479454	6.5	18.583333333333332

2.3 Bug分析

第二次作业中出现的bug是在解析函数定义的时候,没有考虑空白字符
- 这个bug属于预处理阶段的小bug
发现他人的明显bug有:将sin(-t)**n无脑转化为-sin(t)**n,而没有考虑n为奇数还是偶数
错误大都是出自优化的过程中

3.第三次作业

3.1 设计思路

第二次作业已经可以保证输出结果的正确性,但有时会多输出一对括号,会略微影响性能.
基于第二次作业增加了一个拆括号的功能, 思路为先判断表达式因子是否只有一个Term,该Term中是否只有一个非表达式的Factor, 如果是,就把 Expr直接"降级"为相应的非表达式因子,从而解决过度包装

3.2 Bug分析

第三次作业中出现了第二次作业的祖传bug, 即sum函数中i为负数时的代入没有加括号.
- 该bug产生于function.SumFun.callFunction(String) 复杂度: 8.0 3.0 4.0 5.0,其实复杂度并不算高, 主要是因为没加括号导致的bug.
发现他人bug为: 三角函数内部优化时会丢失一些系数, sum的上下限用int储存

4. 总结

找BUG的方式: 采用正则表达式xeger生成数据, 用sympy检测正确性. 遗憾的地方在于生成数据的正则表达式可能不太全面,导致有的bug测不到. 而且有时候生成的hack数据是非法的. 本来以为hack到了结果最后发现是生成的数据有问题.
心得体会:
- 多看讨论区大佬的帖子.
- 在做第一次作业时要勇于把简单问题复杂化,方便后续的迭代开发.
- 认真阅读题目细节.

posted @ 2022-03-22 23:13 IIlIllIIlII 阅读(94) 评论(0) 编辑收藏举报

刷新页面返回顶部

lIIlIIlIIlIIlI

BUAA OO 2022 第一单元总结

BUAA OO 2022 第一单元总结

前言

1. 第一次作业

1.1 设计思路

1.2 代码度量分析

1.3 Bug分析

2. 第二次作业

2.1 设计思路

自定义函数: 由于自定义函数都是简单函数,与其把它当作函数,不如把他当作C中的函数宏去解析.

2.2 代码度量分析

2.3 Bug分析

3.第三次作业

3.1 设计思路

3.2 Bug分析

4. 总结

公告