分类算法学习笔记

机器学习快速入门视频：https://www.bilibili.com/video/av39137333

3 分类算法

3.1 sklearn转换器和估计器

3.1.1 转换器 ——特征工程的父类

特征工程的步骤：

1.实例化（实例化的是一个转换器类（Transformer））
2.调用fit_transform（对文档建立分类词频矩阵，不能同时调用）

　　fit_transform()有fit()和transform()两个方法封装而成。

　　fit() 计算每一列的平均值和标准差

　　transform() 用fit()计算出的结果进行最终转换

3.1.2 估计器（estimator）（sklearn机器学习算法的实现）

估计器工作流程：

实例化一个estimator
estimator.fit(x_train，y_train) 计算传入训练集的特征值和训练集的目标值 ——调用完毕，模型生成
模型评估：

1）直接比对真实值和预测值 y_predict = estimator.predict(x_test)

y_test == y_predict

2）计算准确率

accuracy = estimator.score(x_test,y_test) 传入测试集的特征值和目标值

3.2 K-近邻算法

3.2.1 什么是K-近邻算法（KNN）

KNN核心思想：根据你的“邻居”来推断出你的类别

K- 近邻算法（KNN）原理

K Nearest Neighbor算法又叫KNN算法

定义：如果一个样本在特征空间中的K个最相似（即特征空间中最邻近的样本中的大多数属于某一类别，则该样本也属于这个类别（K = 1（过小）容易受到异常点的影响；K过大，会受到样本不均衡的影响）

如何确定谁是邻居？→ 计算距离 → 距离公式：欧氏距离、曼哈顿距离（绝对值距离）、明可夫斯基距离

3.2.2 K-近邻算法API

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5,algorithm='auto')
- n_neighbors:int，可选（默认 = 5），n_neighbors查询默认使用的邻居数
- algorithm：{'auto','ball_tree','kd_tree','brute'}，可选用于计算最近邻居的算法：‘ball_tree’将会使用BallTree，'kd_tree'将使用KDTree。'auto'将尝试根据传递的fit方法的值来决定最合适的算法。（不同实现方法影响效率）

3.2.3 数据计算

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier

def knn_iris():
    """
    用KNN算法对鸢尾花进行分类
    :return:
    """
    # 1）获取数据
    iris = load_iris()

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data,iris.target, random_state=6)

    # 3）特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）KNN算法预估器
    estimator = KNeighborsClassifier(n_neighbors=3)
    estimator.fit(x_train,y_train)

    # 5）模型评估
    # 方法1：直接对比真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n",y_predict)
    print("直接对比真实值和预测值：\n",y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test,y_test)
    print("准确率为：\n",score)

    return None

if __name__ == "__main__":
    knn_iris()

knn_iris

3.2.4 K-邻近总结

优点：简单，易于理解，易于实现，无需训练
缺点：
- 必须指定K值，K值选择不当则分类精度不能保证
- 懒惰算法，对测试样本分类时的计算量大，内存开销大
使用场景：小数据场景，几千~几万样本，具体场景具体业务去测试

3.3 模型选择与调优

3.3.1 什么是交叉验证

交叉验证：将拿到的训练数据，分为测试和验证集。

将数据分成n份，其中一份作为验证集，然后经过n次测试，每次更换不同的验证集。即得到n组模型的结果，取平均值作为最终结果。又称n折交叉验证。

1 分析

为了让从训练得到模型结果更加准确，所以做以下处理：

训练集：训练集+验证集
测试集：测试集

2 为什么需要交叉验证

交叉验证目的：为了让评估的模型更加准确可信

3.3.2 超参数搜索-网络搜索（Grid Search）

超参数：需要手动指定的参数。

但是手动过程繁杂，所以需要对模型预设几种超参数组合。每组超参数都采用交叉验证来进行评估。最后选出最优参数组合建立模型。

模型选择与调优 API

sklearn.model_selection.GridSearchCV(estimator,param_grid=None,cv=None)
- 对估计器的指定参数值进行详尽搜索
- estimator：估计器对象
- param_grid：估计器参数(dict){"n_neighbors":{1,3,5}}
- cv:指定几折交叉验证
- fit()：输入训练数据
- score()：准确率
- 结果发现：
  - 最佳参数：best_params_
  - 最佳结果：best_score_
  - 最佳估计器：best_estimator_
  - 交叉验证结果：cv_results_

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.model_selection import GridSearchCV

def knn_iris_gscv():
    """
    用KNN算法对鸢尾花进行分类,添加网格搜索和交叉验证
    :return:
    """
    # 1）获取数据
    iris = load_iris()

    # 2）划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data,iris.target, random_state=6)

    # 3）特征工程：标准化
    transfer = StandardScaler()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)

    # 4）KNN算法预估器
    estimator = KNeighborsClassifier()

    # 加入网格搜索和交叉验证
    param_dict = {"n_neighbors": [1, 3, 5, 7, 9, 11]}
    estimator = GridSearchCV(estimator,param_grid=param_dict,cv=10)
    estimator.fit(x_train,y_train)

    # 5）模型评估
    # 方法1：直接对比真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n",y_predict)
    print("直接对比真实值和预测值：\n",y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test,y_test)
    print("准确率为：\n",score)

    # - 最佳参数：best_params_
    print("最佳参数：\n",estimator.best_params_)
    # - 最佳结果：best_score_
    print("最佳结果：\n",estimator.best_score_)
    # - 最佳估计器：best_estimator_
    print("最佳估计器：\n",estimator.best_estimator_)
    # - 交叉验证结果：cv_results_
    print("交叉验证结果：\n",estimator.cv_results_)

    return None

if __name__ == "__main__":
    knn_iris_gscv()

knn_iris_gscv

Facebook案例：

https://www.bilibili.com/video/av39137333?p=23 https://www.bilibili.com/video/av39137333?p=24

3.4 朴素贝叶斯算法

3.4.1 什么是朴素贝叶斯算法分类方法

朴素贝叶斯算法正是利用信息求解后验概率,并依据后验概率的值来进行分类。

朴素（假设特征与特征之间是相互独立的） + 贝叶斯（贝叶斯公式）

应用场景：文本分类（文本分析）（因为单词作为特征）

3.4.2 概率基础

1 概率定义

概率定义为一件事件发生的可能性
P(X)：取值在[0,1]

3.4.3 联合概率、条件概率与相互独立

联合概率：包含多个条件，且所有条件同时成立的概率
- 记作：P(A,B)
条件概率：就是事件A在另外一个事件B已经发生的条件下的发生概率
- 记作：P(A|B)
相互独立：如果P(A,B)=P(A)P(B)，则称事件A与事件B相互独立

3.4.4 贝叶斯公式

1 公式

注：W为给定文档的特征值（频数统计，预测文档提供），C为文档类别

2 这个公式如果应用在文章分类场景中，我们可以这样看

公式可以理解为

其中C可以是不同类别

公式分为三部分：

P(C)：每个文档类别的概率（某文档类别数/总文档数量）
P(W|C)：给定类别下特征（被预测文档中出现的词）的概率
- 计算方法：P(F1|C)=Ni/N（训练文档中去计算）
  - Ni为该F1词在C类别所有文档中出现的次数
  - N为所属类别C下的文档所有词出现的次数和
P(F1,F2,...)预测文档中每个词的概率

3 文章分类计算

可能会计算出某个概率为0

4 拉普拉斯平滑系数

目的：防止计算出的分类概率为0

α为指定的系数一般为1，m为训练文档中统计出的特征词个数

3.4.5 API

sklearn.naive_bayes.MultinomailNB(alpha=1.0)
- 朴素贝叶斯分类
- alpha：拉普拉斯平滑系数

3.4.6 案例

1 步骤

　　1）获取数据

　　2）划分数据集

　　3）特征工程 TFIDF进行文本特征抽取

　　4）朴素贝叶斯预估器流程

　　5）模型评估

2 代码

from sklearn.datasets import fetch_20newsgroups
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB

def nb_news():
    """
    用朴素贝叶斯算法对新闻进行分类
    :return:
    """
    # 1 获取数据
    news = fetch_20newsgroups(subset="all")
    
    # 2 划分数据集
    x_train, x_test, y_train, y_test = train_test_split(news.data,news.target)
    
    # 3 特征工程：文本特征抽取-tfidf
    transfer = TfidfVectorizer()
    x_train = transfer.fit_transform(x_train)
    x_test = transfer.transform(x_test)
    
    # 4 朴素贝叶斯算法预估器流程
    estimator = MultinomialNB()
    estimator.fit(x_train,y_train)
    
    # 5 模型评估
    # 方法1：直接对比真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n",y_predict)
    print("直接对比真实值和预测值：\n",y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test,y_test)
    print("准确率为：\n",score)
    
    return None

nb_news

3.4.7 朴素贝叶斯算法总结

优点：
- 朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。
- 对缺失数据不太敏感，算法也比较简单，常用于文本分类
- 分类准确度高（相对而言），速度快
缺点：
- 由于使用了样本属性独立性的假设，所以如果特征属性有关联时其效果不好

3.5 决策树

3.5.1 认识决策树

如何高效进行决策？

特征的先后顺序

3.5.2 决策树分类原理详解

1 原理

信息论基础
- 信息：消除随机不定性的东西
- 信息的衡量——信息量——信息熵

2 信息熵的定义

H的专业术语称之为信息熵，单位为比特。

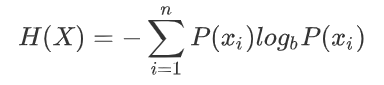
3 决策树的划分依据之一——信息增益

定义与公式特征A对训练数据集D的信息增益g(D,A)，定义为集合D的信息熵H(D)与特征A给定条件下D的信息条件熵H(D|A)之差，
即公式为： $$

公式的详细解释：

信息熵的计算：

条件熵的计算：

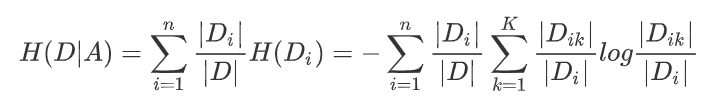
注：Ck表示属于某个类别的样本数

信息增益表示得知特征X的信息不确定性减少的程度使得类Y的信息熵减少的程度

决策树的原理不止信息增益这一种，还有其他方法。

ID3
- 信息增益最大的准则
C4.5
- 信息增益比最大的准则
CART
- 分类树：基尼系数最小的准则在sklearn中可以选择划分的默认原则
- 优势：划分更加细致

3.5.3 决策树API

class sklearn.tree.DecisionTreeClassifier(criterion='gini',max_depth=None,random_state=None)
- 决策树分类器
- criterion：默认是'gini'系数，也可以选择信息增益的熵'entropy'
- max_depth：数的深度大小
- random_state：随机数种子

3.5.4 案例

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier

def decision_iris():
    """
    用决策树对鸢尾花进行分类
    :return:
    """
    # 1 获取数据集
    iris = load_iris()

    # 2 划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)

    # 3 决策树预估器
    estimator = DecisionTreeClassifier(criterion="entropy")
    estimator.fit(x_train, y_train)

    # 4 模型预估
    # 方法1：直接对比真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接对比真实值和预测值：\n", y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)

    return None

if __name__ == "__main__":
    decision_iris()

decision_iris

3.5.5 决策树可视化

1 保存树的结构到dot文件

sklearn.tree.export_graphviz()该函数能够导出DOT格式
- tree.export_graphviz(estimator.out_file='tree.dot（文件路径）',feature_names=['',''])

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier,export_graphviz

def decision_iris():
    """
    用决策树对鸢尾花进行分类
    :return:
    """
    # 1 获取数据集
    iris = load_iris()

    # 2 划分数据集
    x_train, x_test, y_train, y_test = train_test_split(iris.data, iris.target, random_state=22)

    # 3 决策树预估器
    estimator = DecisionTreeClassifier(criterion="entropy")
    estimator.fit(x_train, y_train)

    # 4 模型预估
    # 方法1：直接对比真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n", y_predict)
    print("直接对比真实值和预测值：\n", y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test, y_test)
    print("准确率为：\n", score)
    
    #可视化决策树
    export_graphviz(estimator, out_file="iris_tree.dot",feature_names=iris.feature_names)
    return None

if __name__ == "__main__":
    decision_iris()

决策树可视化

3.5.6 决策树总结

优点：
- 简单，易于理解，可视化
缺点：
- 决策树学习者可能创建不能很好地推广数据过于复杂的数，这被称为过拟合。（容易产生过拟合）
改进：
- 剪枝car算法（决策树API中已经实现）
- 随机森林

3.6 集成学习方法之随机森林

3.6.1 什么是集成学习方法

集成学习通过建立几个模型组合的来解决单一预测问题，它的工作原理是生成多个分类器/模型，各自独立地学习和作出预测，这些预测最后结合成组合预测，因此优于任何一个单分类做出的预测。

3.6.2 什么是随机森林

随机森林是一个包含多个决策树的分类器，并且其输出的类别是由个别树输出的类别的众数而定。

3.6.3 随机森林原理过程

随机：

两个随机：
- 训练集随机 —N个样本中随机有放回的抽样N个
  - bootstrap 随机有放回抽样
- 特征随机 —从M个特征中随机抽取m个特征
  - M >> m 降维

3.6.4 API

class sklearn.ensemble.RandomForestClassifier(n_estimators=10,criterion='gini',max_depth=None,bootstrap=True,random_state=None,min_samples_split=2)
- 随机森林分类器
- n_estimators：integer，optional（default=10）森林里的树木数量120，200,300,500,800,1200
- criterion：string，可选（default='gini'）分割特征的测量方法
- max_depth：integer或None，可选（默认= 无）数的最大深度5,8,15,25,30
- max_features="auto"，每个决策树的最大特征数量
  - if "auto",then max_features = sqrt(n_feature).
  - if "sqrt",then max_features = sqrt(n_feature)(same as "auto").
  - if "log2",then max_features = log2(n_feature).
  - if None,then max_features = n_feature.
- bootstrap：boolean，optional（default = True）是否在构建树时使用放回抽样
- min_samples_split：节点划分最少样本数
- min_samples_leaf：叶子节点的最小样本数
超参数：n_estimator,max_depth,min_samples_split,min_samples_leaf

3.6.5 随机森林预测案例

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import GridSearchCV

    estimator = RandomForestClassifier()

    # 加入网格搜索和交叉验证
    param_dict = {"n_estimators": [120, 200, 300, 500, 800, 1200]}
    estimator = GridSearchCV(estimator,param_grid=param_dict,cv=3)
    estimator.fit(x_train,y_train)

    # 5）模型评估
    # 方法1：直接对比真实值和预测值
    y_predict = estimator.predict(x_test)
    print("y_predict:\n",y_predict)
    print("直接对比真实值和预测值：\n",y_test == y_predict)

    # 方法2：计算准确率
    score = estimator.score(x_test,y_test)
    print("准确率为：\n",score)

    # - 最佳参数：best_params_
    print("最佳参数：\n",estimator.best_params_)
    # - 最佳结果：best_score_
    print("最佳结果：\n",estimator.best_score_)
    # - 最佳估计器：best_estimator_
    print("最佳估计器：\n",estimator.best_estimator_)
    # - 交叉验证结果：cv_results_
    print("交叉验证结果：\n",estimator.cv_results_)

随机森林

3.6.6 总结

在当前所有算法中，具有极好的准确率
能够有效地运行在大数据集上，处理具有高维特征的输入样本，而且不需要降维
能够评估各个特征在分类问题上的重要性

posted @ 2020-02-08 18:12 19呀阅读(248) 评论(0) 编辑收藏举报

刷新页面返回顶部

L19

分类算法 学习笔记