机器学习概述 & 特征工程 学习笔记

机器学习快速入门视频：https://www.bilibili.com/video/av39137333

1.2 什么是机器学习

1.2.1 定义

机器学习是从数据中自动分析获得模型，并利用模型对未知数据进行预测.

从历史数据获得规律 → 数据格式

1.2.2 数据集构成

  • 结构：特征值+目标值

    • 有些数据集可以没有目标值

1.3机器学习算法分类

　　监督学习： 目标值为类别时 →分类问题 

　　　　　　　　算法：K-近邻算法、贝叶斯分类、决策树与随机森林、逻辑回归 

　　　　　　　目标值为连续型数据时 →回归问题 

　　　　　　　　算法：线性回归、岭回归 

　　无目标值 → 无监督学习

　　　　　　　　 算法：聚类K-means

1.4 机器学习开发流程

  1. 获取数据

  2. 数据处理

  3. 特征工程

  4. 使用机器学习算法进行训练

  5. 模型评估 不行的话→2循环

  6. 应用

 

1.5 学习框架和资料介绍

需要明确：

  1. 算法是核心，数据与计算是基础

  2. 找准定位

书： 机器学习（西瓜书） - 周志华

　　 统计学方法 - 李航

　　 深度学习（花书）

2.1 数据集

2.1.1 可用数据集

数据集： 1.sklearn Scikit-learn 　　 2.kaggle 　　 3.UCI

Scikit-learn的使用视频： https://www.bilibili.com/video/av39137333?p=7

 

2.1.3 数据集的划分

机器学习一般的数据集会划分为两个部分：

  • 训练数据：用于训练，构建模型

  • 测试数据：在模型检验时使用，用于评估模型是否有效

划分比例：

  • 训练集：70% ~ 80%

  • 测试集：20% ~ 30%

 

训练集特征值，测试集特征值，训练集目标值，测试集目标值，测试集目标值

x_train，x_test，y_train，y_test

 

2.2 特征工程介绍

2.2.1 什么是特征工程

特征工程是使用专业背景知识和技巧处理数据，使得特征能在机器学习算法上发挥更好的作用的过程。

  • 意义：会直接影响机器学习的效果

2.2.1 特征工程的位置与数据处理的比较

sklearn 特征工程

pandas 数据清洗、数据处理

特征工程包含内容

  • 特征抽取/特征提取

  • 特征预处理

  • 特征降维

2.3 特征抽取

机器学习方法 → 统计方法 → 数学公式

什么是特征抽取： 需要将文本类型转换为数值 文本类型→数值 类型→数值

2.3.1 特征提取

1. 将任意数据（如文本或图像）转换为可用于机器学习的数字特征

注：特征值化是为了让计算机更好的去理解数据

  • 字典特征提取（特征离散化）

  • 文本特征提取

  • 图像特征提取（深度学习）

2. 特征提取API

sklearn.feature_extraction

2.3.2 字典特征提取

作用：对字典数据进行特征值化

  • sklearn.feature_extraction.DictVectorizer(sparse = True...)

    • DictVectorizer.fit_transform(X) X：字典或者包含字典的迭代器 返回值：返回sparse（稀疏）矩阵 稀疏矩阵：按位置将非零值表示出来 节省内存 → 提高加载效率

    • DictVectorizer.inverse_transform(X) X:array数组或者sparse矩阵 返回值：转换之前数据格式

    • DictVectorizer.get_feature_names() 返回类别名称

1.应用

将类别 转换为 one-hot编码

2.流程分析

  • 实例化类DictVectorizer

  • 调用fit_transform方法输入数据并转换（注意返回格式）

 

from sklearn.feature_extraction import DictVectorizer
​
def dict_demo():
    """
    对字典型的数据进行特征抽取
    :return: None
    """
    data = [{'city':‘北京’，‘temperature’：100},{'city':‘上海’，‘temperature’：60},{'city':‘深圳’，‘temperature’：30}]
    # 1. 实例化一个转换器类
    transfer = DictVectorizer(sparse = False)
    # 2. 调用fit_transform
    data = transfer.fit_transform(data)
    print("返回结果：\n",data);
    # 打印特征名字
    print("特征名字  \n",transfer.get_feature_names())
    
    return None
DictVectorizer_demo

 

注意 sparse = False

应用场景

1. 数据集中有很多类别特征 → 将数据集中的特征转化为字典类型 →DictVectorizer转换
2. 本身拿到的数据就就是字典类型

2.3.3 文本特征提取

作用：对文本数据进行特征值化

  • sklearn.feature_extraction.text.CountVectorizer(stop_word=[]) stop_work 停用词

    • 返回词频矩阵

  • CountVectorizer.fit_transform(X) X:文本或者包含文本字符串的可迭代对象 返回值：返回sparse矩阵

  • CountVectorizer.inverse_transform(X) X:array数组或者sparse矩阵 返回值：转换之前的数据格

  • CountVectorizer.get_feature_names() 返回值：单词列表

  • sklearn.feature_extraction.text.TfidfVectorizer 关键词：在某一个类别中的文章中，出现的次数很多，但是在其他类别的文章中出现很少

CountVectorizer

from sklearn.feature_extraction import CountVectorizer
​
def count_demo():
    """
    文本特征抽取：CountVectorizer
    :return: None
    """
    data = ["life is short,i like like python","Life is too long.i dislike python"]
    # 1. 实例化一个转换器类
    transfer = CountVectorizer() //没有sparse = False这个参数
    # 2. 调用fit_transform
    data = transfer.fit_transform(data)
    print("返回结果：\n",data.toarray)
    # 打印特征名字
    print("特征名字  \n",transfer.get_feature_names())
    
    return None
count_demo

 

如果处理中文需要先进行分词（用空格隔开）（不支持单个汉字）

import jieba
def cut_word(text):
    """
    进行中文分词 "我爱北京天安门" → "我 爱 北京 天安门"
    """
    return " ".join(list(jieba.cut(text)))

 

Tf-idf文本特征提取

  • TF-IDF的主要思想：如果某个词或短语在一篇文章中出现的频率高，并且在其他文章中很少出现，则认为此词或者短语具有很好的类别区分能力，适合用来分类。

  • TF-IDF作用：用以评估一字词对于一个文件集或一个语料库中的其中一份文件的重要程度。

公式

  • 词频（term frequency，tf）指的是某一个给定的词语在该文中出现的频率

  • 逆向文档频率（inverse document frequency，idf)是一个词语普遍重要性的度量。某一特定词语的idf，可以由总文件数目除以包含该词语的文件的数目，再将得到的商取以10为底的对数得到

​

最终得出结果可以理解为重要程度。

例：

1000篇文章 ——语料库

其中 100篇文章 —— “非常”

10篇文章 —— “经济”

两篇文章：

文章A（100词）：10次“经济” TF-TDF:0.2

tf:10/100 = 0.1

idf: l0g(10) 1000/10 = 2

文章B（100词）：10次“非常” TF-IDF：0.1

tf:10/100 = 0.1

idf:log(10) 1000/100 = 1

2.4 特征预处理

2.4.1 什么是特征预处理

通过一些转换函数将特征数据转换成更加适合算法模型的特征数据过程

1 包含内容

  • 数值型数据的无量纲化：

    • 归一化

    • 标准化

2 特征预处理API

sklearn.preprocessing

为什么我们要进行归一化/标准化？

  • 特征的单位或者大小相差较大，或者某特征的方差相比其他的特征要大出几个数量级，容易影响（支配）目标结果，使得一些算法无法学习到其它的特征

2.4.2 归一化

1 定义

通过对原始数据进行变换把数据映射到（默认为[0,1]）之间

2 公式

3 API

  • sklearn.preprocessing.MinmaxScaler(feature_range=(0,1)...)

    • MinMaxScalar.fit_transform(X)

      • X:numpy array格式的数据[n_samples,n_features]

    • 返回值：转换后的形状相同的array

4 数据计算

  • 分析

  1. 实例化MinMaxScalar

  2. 通过fit_transform转换

import pandas as pd
from sklearn.preprocessing import MinMaxScaler
​
def minmax_demo():
    """
    归一化
    """
    # 1. 获取数据
    data = pd.read_csv("文件名")
    data = data.iloc[:, :3]
    print("data:\n",data)
    
    # 2. 实例化一个转换器类
    transfer = MinMaxScaler()
    # transfer = MinMaxScaler(feature_range=[2,3])  不写时默认为0,1
    
    # 3. 调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n",data_new)
    
    return None
minmax_demo

 

5 归一化总结

最大最小值是变化的，另外，最大值最小值非常容易受异常点影响，所以这种方法只适合传统精确小数据场景。

 

2.4.3 标准化

1 定义

通过对原始数据进行变换把数据变换到均值为0，标准差为1范围内

2 公式

​ 作用于每一列，mean为平均值，σ为标准差

  • 对归一化来说：如果出现异常点。影响了最大值和最小值，那么结果显然会发生改变。

  • 对标准化来说：如果出现异常点，由于具有一定数据量，少量的异常点对于平均值的影响并不大，从而方差改变比较小。

3 API

  • sklearn.preprocessing.StandardScaler()

    • 处理之后，对每列来说，所有数据都聚集在均值为0附近，标准差为1

    • StandardScaler.fit_transform(X)

      • X:numpy array格式的数据[n_samples,n_features]

    • 返回值：转换后的形状相同的array

4 数据计算

  • 分析

  1. 实例化StandardScaler

  2. 通过fit_transform转换

import pandas as pd
from sklearn.preprocessing import StandardScaler
​
def stand_demo():
    """
    标准化
    """
    # 1. 获取数据
    data = pd.read_csv("文件名")
    data = data.iloc[:, :3]
    print("data:\n",data)
    
    # 2. 实例化一个转换器类
    transfer = StandardScaler()
    
    # 3. 调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n",data_new)
    
    return None
stand_demo

 

5 标准化总结

在已有样本足够多的情况下比较稳定，适合现代嘈杂大数据场景。

 

2.5 特征降维

2.5.1 降维

降维是指在某些限定条件下，降低随机变量（特征）个数，得到一组“不相关”主变量的过程

2.5.2 降维的两种方式

  • 特征选择

  • 主成分分析（可以理解一种特征提取的方式）

2.5.3 什么是特性选择

1 定义

数据中包含冗余或相关变量（或称特征、属性、指标等），旨在从原有特征中找出主要特征。

2 方法

  • Filter（过滤式）：主要探究特征本身特点、特征与特征和目标值之间关联

    • 方差选择法：低方差特征过滤

    • 相关系数 - 特征与特征之间的相关程度

  • Embedded（嵌入式）：算法自动选择特征（特征与目标值之间的关联）

    • 决策树：信息熵、信息增益

    • 正则化：L1、L2

    • 深度学习：卷积等

3 模块

sklearn.feature_selection

4 过滤式

4.1 低方差特征过滤

删除低方差的一些特征

  • 特征方差小：某个特征大多样本值比较相近

  • 特征方差大：某个特征很多样本的值都有区别

API

  • sklearn.feature_selection.VarianceThreshold(threshold = 0.0)

    • 删除所有低方差特征

    • Variance.fit_transform(X)

      • X:numpy array格式的数据[n_samples,n_features]

      • 返回值：训练集差异低于threshold的特征将被删除。默认值是保留所有非零方差特征，即删除所有样本中具有相同值的特征。

数值计算

  • 分析

    • 初始化VarianceThreshold，指定阈值方差

    • 调用fit_transform

from sklearn.feature_selection import VarianceThreshold
​
def variance_demo():
    """
    过滤低方差特征
    删除低方差特征——特征选择
    """
    # 1. 获取数据
    data = pd.read_csv("文件名")
    data = data.iloc[:, 1:-2]
    print("data:\n",data)
    # 2. 实例化一个转换器类
    transfer = VarianceThreshold()
    #transfer = VarianceThreshold(threshold=5)根据需求设阈值 
    
    # 3. 调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n",data_new)
    
    return None
variance_demo

 

4.2 相关系数

  • 皮尔逊相关系数（Pearson Correlation Coefficient)

    • 反映变量之间相关关系密切程度的统计指标

公式（了解，不用记忆）

​

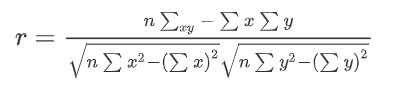
特点

相关系数的值介于-1与+1之间，即-1≤ r ≤+1，其性质如下：

  • 当r > 0时，表示两变量正相关，r ＜ 0时，两变量负相关

  • 当|r| = 1时，表示两变量为完全相关，当 r = 0时，表示两变量间无相关关系

  • 当0<|r|<1时，表示两变量存在一定程度的相关，且|r|越接近1，两变量间线性关系越密切；|r|越接近于0，表示两变量的线性相关越弱

  • 一般可按三级划分：|r|＜0.4为低度相关；0.4≤|r|＜0.7为显著性相关；0.7≤|r|＜1为高度线性相关

API

  • from scipy.stats import pearsonr

    • x:(N.) array_like

    • y:(N.) array_like Returns:(Pearson's coefficient,p-value)

from sklearn.feature_selection import VarianceThreshold
from scipy.stats import pearsonr
​
def variance_demo():
    """
    过滤低方差特征
    删除低方差特征——特征选择
    """
    # 1. 获取数据
    data = pd.read_csv("文件名")
    data = data.iloc[:, 1:-2]
    print("data:\n",data)
    # 2. 实例化一个转换器类
    transfer = VarianceThreshold()
    #transfer = VarianceThreshold(threshold=5)根据需求设阈值 
    
    # 3. 调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n",data_new)
    
    #计算某两个变量之间的相关
    r = pearsonr(data["pe_ratio"], data["pb_ratio"])
    print("相关系数：\n",r)
    
    return None
variance_demo

 

特征与特征之间相关性很高时：

1） 选取其中一个

2）加权求和作为一个新的特征

3）主成分分析

2.5.4 主成分分析

2.5.4.1 什么是主成分分析（PCA）

  • 定义：高维数据转化为低维数据的过程，在此过程中可能会舍弃原有数据、创造新的变量。

  • 作用：数据维数压缩，尽可能降低原数据的维数（复杂度），损失少量信息。

  • 应用：回归分析或者聚类分析当中

找到一个合适的直线，通过一个矩阵运算得出主成分分析的结果。

2.5.4.2 API

  • sklearn.decomposition.PCA(n_components = None)

    • 将数据分解为较低维数空间

    • n_components：

      • 小数：表示保留百分之多少的信息

      • 整数：减少到多少特征

    • PCA.fit_transform(X) X:numpy array格式的数据[n_samples,n_features]

    • 返回值：转换后指定维度的array

2.5.4.3 数据计算

form sklearn.decomposition import PCA
​
def pca_demo():
    """
    PCA降维
    """
    data = [[2,8,4,5],[6,3,0,8],[5,4,9,1]]
    
    # 1.实例化一个转换器类
    transfer = PCA(n_components=2)
    
    # 2.调用fit_transform
    data_new = transfer.fit_transform(data)
    print("data_new:\n",data_new)
    
    return None
pca_demo

 

 

posted @ 2020-02-06 16:12  19呀  阅读(141)  评论(0)  编辑  收藏  举报