2018 东北地区大学生程序设计竞赛(ABEHIK)
HDU6500:Problem A. Game with string
题意:
给你一个字符串s以及它的m个子串的首尾位置,现在Alice和 Bob两个人轮流在任一子串的前面或者后面加1个字符,要求加了这个串加了一个字符之后仍然是s的子串,谁不能加了谁就输了,要你输出谁赢。
题解:
每个子串可以加的字符次数是恒定的:s串的长度-子串的长度。那么我们将所有子串可以加的次数加起来再判断奇偶就能得出答案。
傻逼多组WA了几发
代码:

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 100000+10; const int INF = 1e9+10; const ll mod = 998244353; int main() { string s; while (cin>>s){ int len = s.length(); int n,l,r,sum = 0; scanf("%d",&n); for (int i = 0; i < n; i++){ scanf("%d%d",&l,&r); sum += len - (r-l+1); } if (sum&1) printf("Alice\n"); else printf("Bob\n"); } return 0; }
HDU6501:Problem B. Memory Banks
题意:
有60种不同种类的内存存储区,编号为0~59,第i种内存存储区的内存大小为2i,告诉你每种内存存储区的数量。
有n个空间站,每个空间站需要wi的内存空间,每个空间站你都要用你已有的内存存储区来为它提供正好wi的内存空间。
如果有空间站不能正好有wi的内存空间输出-1,否则输出你剩下的内存存储区的总存储量。
题解:
要使组成的空间站尽可能多,我们需要先取容量大的。我们可以把每个站需要的内存空间转化为2进制,从高位到低位,如果这i位为1就代表需要1个容量为2i的内存存储区,如果少了可以用2倍的容量为2i-1的内存存储区代替。
例如如果需要10的内存空间,化成2进制就是1010,需要1个23和1个21,若没有容量为23的可以用两个容量为22的代替。
如果当前空间站内存不够,则输出-1,否则求各个类型剩余容量与个数的乘积之和。
代码:

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 100000+10; const int INF = 1e9+10; const ll mod = 1e9+7; ll qp(ll a, ll b){ ll ans = 1; while (b) { if (b&1) ans = (ans * a) % mod; a = (a * a) % mod; b >>= 1; } return ans; } ll a[70]; int main() { while (~scanf("%lld",&a[0])) { for (int i = 1; i < 60; i++) scanf("%lld",&a[i]); int n; scanf("%d",&n); bool fg = 1; while (n--) { ll w,sum = 0; scanf("%lld",&w); int cnt = 0,b[70]; while (w) { b[cnt++] = w%2; w>>=1; } for (int i = cnt - 1; i >= 0; i--) { sum = sum * 2 + b[i]; if (!a[i]) continue; if ( sum > a[i]) { sum -= a[i]; a[i] = 0; } else { a[i] -= sum; sum = 0; } } if (sum) fg = 0; } if (!fg) printf("-1\n"); else { ll ans = 0; for (int i = 0; i < 60; i++) { if (a[i]) ans = (ans + (a[i]%mod) * qp(2,i) % mod )%mod; } printf("%lld\n",ans); } } return 0; }
HDU6504:Problem E. Split The Tree
题意:
给你一颗节点由1到n编号的树,告诉你每个点的值Wi 。将树的权重定义为树中 不同的节点的值Wi 的数量。
删掉一条边之后这棵树就变成了两棵树,得分是两颗数的权重和,要你求一棵树拆成两棵树的最大权重和。
题解:
我们可以通过dfs序将这棵树 变成一个线性的,且每个子树在一段连续区间。求树的权重就相当于求一段区间内不同值的数量。
要求删掉一条边之后形成的两棵树的最大权重和。我们可以枚举删每一条边时的权重和,
在每一次计算的时候,我们可以用树状数组维护,将区间扩大一倍,如果删掉边之后一个子树的区间范围为[l,r] ,那么另一个子树区间为[r+1,n+l-1]。计算这两个区间不同节点值数量和即可。
这题也可以用莫队,还没写,待补。
代码:

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 200000 +10; const int INF = 1e9+10; const ll mod = 1e9+7; struct node{ int id,l,r; node() {} node(int id,int l,int r):id(id),l(l),r(r) {} } q[N]; int n,dfsnum; int sum[N], val[N], L[N], R[N], vis[N], ans[N], num[N]; vector<int> edge[N]; bool cmp(node x,node y) { if (x.r != y.r) return x.r < y.r; else return x.l < y.l; } int lowbit(int x) { return x&(-x); } void add(int x,int k) { while (x <= n*2) { sum[x]+=k; x+=lowbit(x); } } int query(int x) { int ans = 0; while (x) { ans += sum[x]; x -=lowbit(x); } return ans; } void dfs(int x) { L[x] = ++dfsnum; num[dfsnum] = num[dfsnum+n] = x; for (int i = 0; i < edge[x].size(); i++) { dfs(edge[x][i]); } R[x] = dfsnum; } int main() { while(~scanf("%d",&n)) { for (int i = 0; i <= n; ++i) { edge[i].clear(); } for (int i = 2; i <= n; i++) { int u; scanf("%d",&u); edge[u].push_back(i); } dfsnum = 0; dfs(1); for (int i = 1; i <= n; i++) { scanf("%d",&val[i]); val[n+i] = val[i]; } int cnt = 0; for (int i = 1; i <= n; i++) { q[++cnt] = node(i,L[i],R[i]); q[++cnt] = node(i,R[i] + 1, n+L[i]-1); } sort(q+1,q+1+cnt,cmp); int maxx = 0, top = 1; memset(vis,0, sizeof(vis)); memset(ans,0, sizeof(ans)); memset(sum,0,sizeof(sum)); for (int i = 1; i <= cnt; i++) { for (int j = top; j <= q[i].r; ++j) { int x = val[num[j]]; if (vis[x]) add(vis[x],-1); vis[x] = j; add(vis[x],1); } top = q[i].r+1; ans[q[i].id] += query(q[i].r) - query(q[i].l - 1); maxx = max(maxx,ans[q[i].id]); } printf("%d\n",maxx); } return 0; }
HDU6507:Problem H. Store The Matrix
题意:
给你一个r*c的矩阵M,它可以分解成多个矩阵相乘:M = A1×A2 · · ·×An (n≥1),每个矩阵Ai的大小为ri*ci。我们通过存这个n个矩阵的元素来存矩阵M,每个矩阵Ai的元素个数为ri*ci,求最少需要存的元素数量。
题解:
这题我的理解是:对于一个矩阵M,你要不就不拆,n=1,存的元素数量为r*c。要不就拆成两个矩阵相乘,我们知道要得到r*c的矩阵,需要两个大小分别为r*x,x*c的矩阵相乘,显然当x为矩阵M的秩时最优。
所以这是一个求矩阵的秩的模板题。
这个题还可以用高斯消元写,待补。
参考博客:https://www.cnblogs.com/letlifestop/p/10819422.html
代码:

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 50+10; const int INF = 1e9+10; const ll mod = 1e9+7; int a[N][N]; int n,m; int r() { int i=0,j=0,k,r,u; while(i<n&&j<m) { r=i; for(k=i; k<m; k++) { if(a[k][j]) { r=k; break; } } if(a[r][j]) { if(r!=i) { for(k=0; k<=n; k++) { swap(a[r][k],a[i][k]); } } for(u=i+1; u<m; u++) { if(a[u][j]) { for(k=i; k<=n; k++) { a[u][k]^=a[i][k]; } } } ++i; } j++; } return i; } int main() { while(~scanf("%d%d",&n,&m)) { for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++){ scanf("%d",&a[i][j]); } } printf("%d\n",min(n*m,max(1,r())*(n+m))); } return 0; }
HDU6508:Problem I. Spell Boost
题意:
你有n张牌,每张牌需要wi点法力,能给敌人造成xi点伤害。卡牌有两种类型,一种是魔法牌,一种是增幅牌。一张牌可能包含这两种类型。每当你使用一张魔法牌的时候,对于每一张未被使用的增幅牌i需要的法力值wi减1。现在你有W点法力,问能造成的最大的伤害值为多少。
题解:
因为魔法牌能降低增幅牌所需的法力值,所以我们可以先按需要值从小到大取魔法牌,然后在从小到大取增幅牌。每件物品只有一件,容量为W,你可以取或者不取,使伤害值最大。类似于背包问题,不过这里的法力值是会减少的。我们可以用dp[i][j][k] 来表示造成的伤害值,i为第i张牌,j为前面使用了多少张增幅牌,k为用了的法力值。因为我们每次选第i张牌都是在前i-1张牌选了之后操作的,我们可以把数组简化成dp[i%2][j][j],节省空间。
代码:

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 500+10; const int INF = 1e9+10; const ll mod = 1e9+7; struct node{ int w,x,is1,is2; }a[N]; int dp[2][N][N]; bool cmp(node i, node j) { if (i.is1 != j.is1) return i.is1 > j.is1; if (i.is2 != j.is2) return i.is2 < j.is2; return i.w < j.w; } int main() { int n,m; while(~scanf("%d%d",&n,&m)) { memset(dp,-1,sizeof(dp)); for (int i = 1; i <= n; i++) { scanf("%d%d%d%d",&a[i].w,&a[i].x,&a[i].is1,&a[i].is2); } sort(a+1,a+n+1,cmp); dp[0][0][0]=0; for (int i = 1; i <= n; i++) { memset(dp[i%2],-1,sizeof(dp[i%2])); for (int j = 0; j <= i; j++) { for (int k = 0; k <= m; k++) { if (dp[(i - 1) % 2][j][k] == -1) continue; dp[i % 2][j][k] = max(dp[i % 2][j][k], dp[(i - 1) % 2][j][k]); int u = j + a[i].is1; //判断是不是魔法牌 int v = k + max(0, a[i].w - j * a[i].is2);//减之前判断需不需要减 if (v <= m) { dp[i % 2][u][v] = max(dp[i % 2][u][v], dp[(i - 1) % 2][j][k] + a[i].x); } } } } int ans = 0; for (int i = 0; i <=n; i++) { for (int j = 0; j<= m; j++) ans = max(ans,dp[n%2][i][j]); } printf("%d\n",ans); } return 0; }
HDU6510:Problem K. Harbin Sausage
题意:
对于下面这个三视图,给你H和R,每单位体积需要花费 3/Pi(圆周率) 问这个几何体花费的总金额。
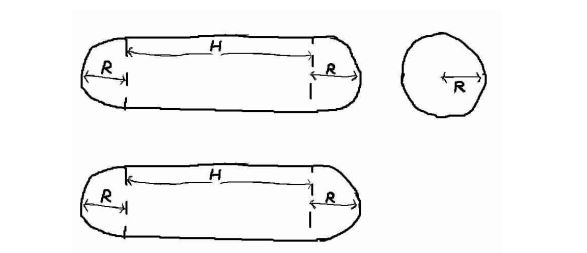
题解:
公式为:(4*Pi*R*R*R/3 + Pi*R*R*H) * 3/Pi = 4*R*R*R+3*R*R*H
代码:

#include <bits/stdc++.h> using namespace std; typedef long long ll; const int N = 100000+10; const int INF = 1e9+10; const ll mod = 998244353; int main() { int h,r; scanf("%d%d",&h,&r); printf("%d",4*r*r*r+3*r*r*h); return 0; }




