JavaScript的数据结构和算法

所有JavaScript对象都有hasOwnProperty(value)的方法，用来返回一个表明对象是不是具有这个value Key值属性的布尔值。

javaScript的方法 具有delete的方法 事实上在业务中很少去删除真实的数据，但是在做一下添加和删除时 为了配合后端 也是会用到的。

 在javaScript中我们通常使用数据结构是对象和数组, 更常用的是链表结构,添加和删除方便，不需要去遍历。这是一个很节省性能的事情。

  new.target 是一个新增的管理 实例函数的方法  如果这个函数被new 或者继承调用 那么就会被返回当前的class或者function 否则返回一个undefined 需要些在constructor里。

 set类 在JavaScript中体现为集合的形式 类似对象不同于对象只能一组一组的保存，是可以多组进行保存的类比其他的语言set类 它算是比较完善的了，set类的结构 类似{1:1,2:2} 以key：value的形式保存起来。 我们可以使用它用来求交集，并集，差集，子集等等 类似于对象所以我们可以使用delete 来它其中的某一项，获取它的长度可以通过 用Object.keys来枚举它拿到这个数组的length。添加可以使用其自己本省所带的add的方法。检测是否有这个属性key 我们可以使用hasOwnProperty()的方法来确认这个属性。 这里的集合存储的是一组互不相同的元素.(也就是说这里不适用多重集)。

 散列表和字典结构 在JavaScript中体现为Map类。顾名思义 主要是为了做映射使用。用来存储唯一的值，结构也是使用key: value的形式。

 非顺序数据结构有散列法和树。

一个树的结构包含一系列的父子关系的节点。每个节点都有一个父节点(除了顶部的第一个节点)以及零个或多个子节点。

 

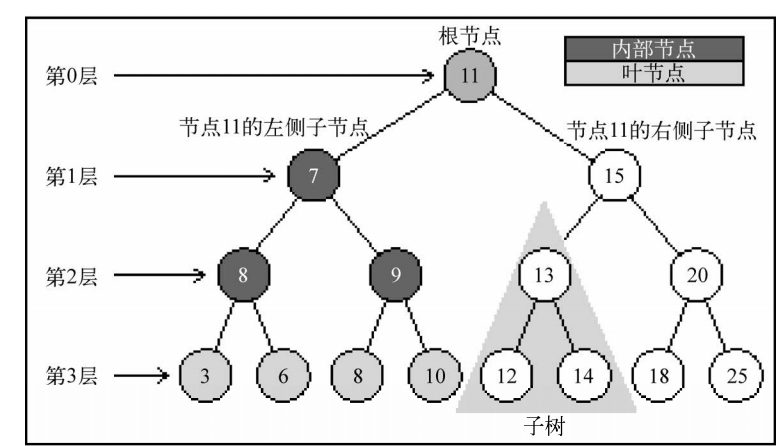
 (这里图的第二层8是错误的 应该是5)

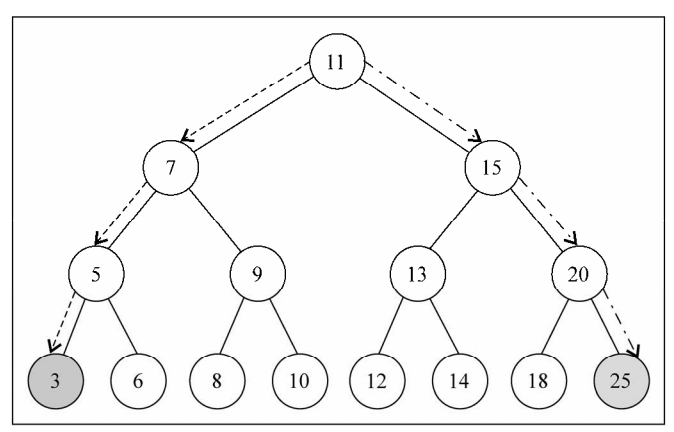
   位于树顶部的节点叫做根节点。它没有父节点。树种的每个元素都叫做节点。节点分为内部节点和外部节点。 至少有一个字节点的节点称为内部节点(7,5,9,15,13,20是内部节点).没有子元素的节点称为外部节点或叶节点(3，6，8，10，12，14，18，25都是叶节点)。

 一个节点可以有祖先和后代。一个节点(除了根节点)的祖先包括父节点,祖父节点,曾祖父节点等等一个节点的后代包括它下面的所有节点。如图上节点9的祖先节点有7和11，而他的字节点有8和10.

  有关于树的另一个术语是子树。子树由节点和它的后代构成。比如节点13和12,14构成了图中的子树。

  节点的一个属性是深度，节点的深度取决于它的祖先节点的数量。比如，节点10有3个祖先节点(9,7,11)，那么它的深度就是3.

 树的高度取决于所有节点深度的最大值。一棵树也可以被分解成层级。根节点在第0层，它的字节点在第一层。

 二叉树和二叉搜索树

二叉树的节点最多只能有两个子节点：一个是左侧子节点，另一个是右侧的子节点。这些定义有助于我们写出更高效的向/从树中插入，查找和删除节点的算法。

 上图就是一个二叉搜索树(BST)。属于二叉树的一种。

  如何用代码去申明一个二叉搜索树。

  首先定义一个function BinarySearchTree类。

   首先:  我们先明确二叉搜索树.

class BinarySearchTree {
  consturtor() {
     this.Node = class {
      consturtor(key){
     　this.key = key; //这是我们的节点值 变量私有化
       this.left = null ; // 根节点起始左位置的初始化
       this.right = null; // 根节点起始右位置的初始化
　　　　}
     }
     this.root = null ; //起始的根节点
  }
}

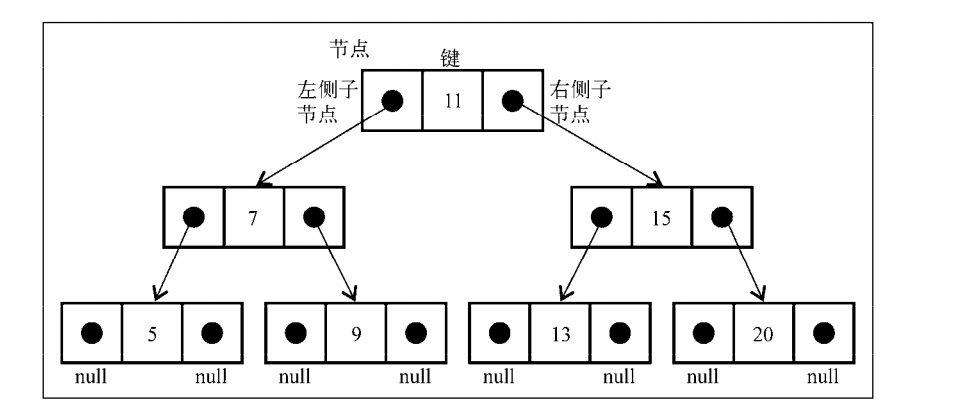
和链表一样，都是通过指针来表示节点之间的关系(术语称为边)。在双向链表中,每个节点都包含两个指针，一个指向下一个节点，一个指向上一个节点。对于树，使用同样的方式(也使用两个指针) 

     class BinarySearchTree {
        constructor() {
          this.Node = class {
            constructor(key){
            　this.key = key; //这是我们的节点值 变量私有化
              this.left = null ; // 根节点起始左位置的初始化
              this.right = null; // 根节点起始右位置的初始化
      　　　　}
          }
          this.root = null ; //起始的根节点
        }
        insert(key) {
          const newNode = new this.Node(key);
          if (this.root === null) {
            this.root = newNode;
          } else {
            this.insertNode(this.root, newNode);
          }
        }
        insertNode(node, newNode) { // 尾递归查询节点
          if (newNode.key < node.key) { //如果新的节点值小于父节点的值
            if (node.left === null) {
              node.left = newNode;
            } else {
              this.insertNode(node.left, newNode);
            }
          } else {
            if (node.right === null) {
              node.right = newNode;
            } else {
              this.insertNode(node.right, newNode);
            }
          }
        }
      }
       const BinarySearchTree1 = new BinarySearchTree();
       BinarySearchTree1.insert(11);
       BinarySearchTree1.insert(7);
       BinarySearchTree1.insert(15);
       BinarySearchTree1.insert(5);
       BinarySearchTree1.insert(3);
       BinarySearchTree1.insert(9);
       BinarySearchTree1.insert(8);
       BinarySearchTree1.insert(10);
       BinarySearchTree1.insert(13);
       BinarySearchTree1.insert(12);
       BinarySearchTree1.insert(14);
       BinarySearchTree1.insert(20);
       BinarySearchTree1.insert(18);
       BinarySearchTree1.insert(25);
       console.log(BinarySearchTree1);

这样我们就实现了 插入的方法。

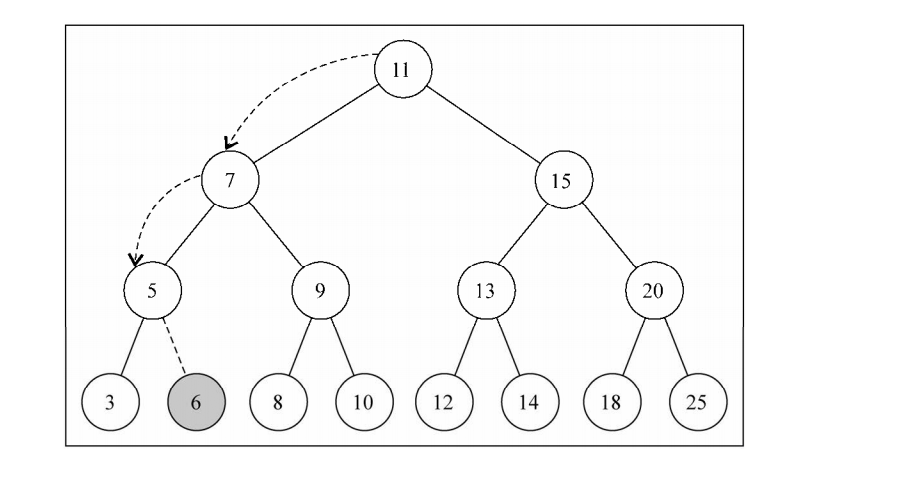
这就是我们得到的二叉树。

树的遍历分为三种 中序遍历 先序遍历 后序遍历

 中序遍历是一种以上行顺序的访问的BST所有节点的遍历方式，也就是以从最小到最大的顺序访问所有节点。中序遍历的一种应用就是对树进行排序操作。

      class BinarySearchTree {
        constructor() {
          this.Node = class {
            constructor(key){
            　this.key = key; //这是我们的节点值 变量私有化
              this.left = null ; // 节点起始左位置的初始化
              this.right = null; // 节点起始右位置的初始化
      　　　　}
          }
          this.root = null ; //起始的根节点
        }
        insert(key) {
          const newNode = new this.Node(key);
          if (this.root === null) {
            this.root = newNode;
          } else {
            this.insertNode(this.root, newNode);
          }
        }
        insertNode(node, newNode) {
          if (newNode.key < node.key) { //如果新的节点值小于父节点的值
            if (node.left === null) {
              node.left = newNode;
            } else {
              this.insertNode(node.left, newNode);
            }
          } else {
            if (node.right === null) {
              node.right = newNode;
            } else {
              this.insertNode(node.right, newNode);
            }
          }
        }
        inOrderTraverseNode(node, callback) {
          if (node !== null) { //{2}
            this.inOrderTraverseNode(node.left, callback); //{3}
            callback(node.key); //{4}
            this.inOrderTraverseNode(node.right, callback); //{5}
          } 
        }
        inOrderTraverse(callback) {
          this.inOrderTraverseNode(this.root, callback);
        }
        printNode(value) {
          console.log(value);
        }
      }
       const BinarySearchTree1 = new BinarySearchTree();
       BinarySearchTree1.insert(11);
       BinarySearchTree1.insert(7);
       BinarySearchTree1.insert(15);
       BinarySearchTree1.insert(5);
       BinarySearchTree1.insert(3);
       BinarySearchTree1.insert(9);
       BinarySearchTree1.insert(8);
       BinarySearchTree1.insert(10);
       BinarySearchTree1.insert(13);
       BinarySearchTree1.insert(12);
       BinarySearchTree1.insert(14);
       BinarySearchTree1.insert(20);
       BinarySearchTree1.insert(18);
       BinarySearchTree1.insert(25);
       BinarySearchTree1.inOrderTraverse(BinarySearchTree1.printNode);
       console.log(BinarySearchTree1);

搜索树中的值

在树中, 有三种经常执行的搜索类型：

最小值；

最大值；

搜索特定的值。

搜索最小值和最大值