c++实现多叉树树形显示(适合家谱的显示)
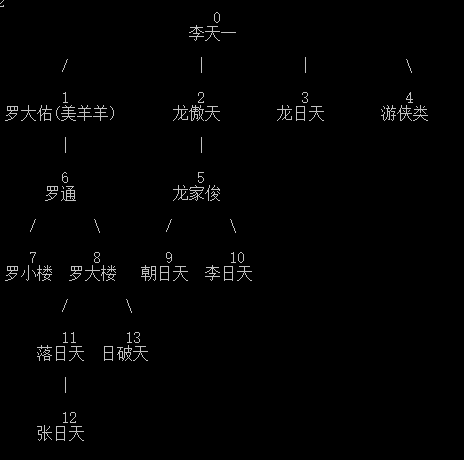
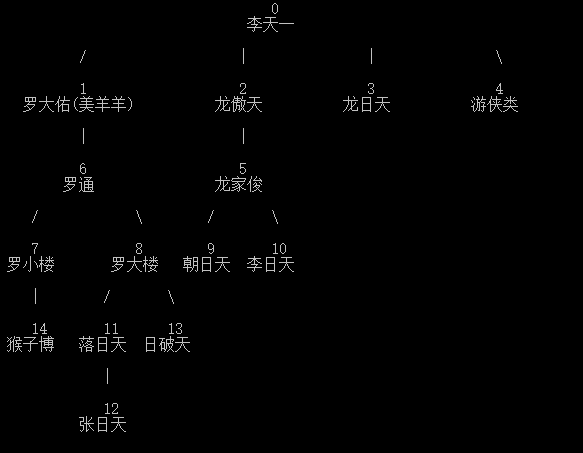
多叉树(左兄弟右孩子二叉树)的树形显示
核心代码
void positionadd(Multiway_tree*root, int n)
{
if (!root)return;
Multiway_tree*pcur = root;
stack<Multiway_tree*>s;
while (pcur || !s.empty())
{
if (pcur)
{
if (pcur == root->brother)break;
pcur->positon += n;
s.push(pcur);
pcur = pcur->child;
}
else
{
pcur = s.top();
s.pop();
pcur = pcur->brother;
}
}
}
void Multiway_tree::display(Multiway_tree *root, const int distance)
{
if (root == NULL)
return;
root->positon = 0;
root->positionmark = " ";
int *namenum = new int[sum];
stack<Multiway_tree*>s;
Multiway_tree *pcur;
pcur = root;
int gener = 0;
while (pcur || !s.empty())
{
if (pcur)
{
if (pcur->generation > gener)gener = pcur->generation;
if (gener)
s.push(pcur);
pcur = pcur->child;
}
else
{
pcur = s.top();
s.pop();
pcur = pcur->brother;
}
}
Multiway_tree **p1 = new Multiway_tree*[gener + 1];
for (int i = 0; i < gener + 1; ++i)
p1[i] = 0;
pcur = root;
while (pcur || !s.empty())
{
if (pcur)
{
if (!(p1[pcur->generation]))p1[pcur->generation] = pcur;
else { Multiway_tree*t = p1[pcur->generation]; while (t->next)t = t->next; t->next = pcur; }
namenum[pcur->num] = pcur->name.size() ;
if (pcur->parent)
if (pcur->parent->child == pcur)
{
Multiway_tree*t = pcur;
if (pcur->brother)pcur->positionmark = "/";
else pcur->positionmark = "|";
t->parent->childrennum++;
while (t->brother)
{
t->parent->childrennum++;
t->brother->positionmark = "|";
t = t->brother;
}
if (t != pcur)t->positionmark = "\\";
}
s.push(pcur);
pcur = pcur->child;
}
else
{
pcur = s.top();
s.pop();
pcur = pcur->brother;
}
}
pcur = root;
pcur->positon = 0;
while (pcur || !s.empty())
{
if (pcur)
{
if (pcur->parent)
{
int n = 0;
if (pcur->parent->child == pcur)
{
Multiway_tree*t = pcur;
pcur->positon = 0;
while (t->brother)
{
t->brother->positon = t->positon + namenum[t->num] + distance;
t = t->brother;
}
int g = t->parent->positon + (namenum[t->parent->num]) / 2 - (t->positon + namenum[t->num]) / 2;
if (t->parent->childrennum == 1)pcur->positon = pcur->parent->positon + namenum[pcur->parent->num] / 2 - namenum[pcur->num] / 2;
else pcur->positon = g;
t = pcur;
while (t->brother)
{
t->brother->positon += g;
t = t->brother;
}
}
}
s.push(pcur);
pcur = pcur->child;
}
else
{
pcur = s.top();
s.pop();
pcur = pcur->brother;
}
}
for (int i = gener; i > 0; --i)
{
for (Multiway_tree*t1 = p1[i]; t1->next; t1 = t1->next)
{
if (t1->parent->child != t1)continue;
for (Multiway_tree*t2 = t1->next; t2; t2 = t2->next)
{
if (t2->parent == t1->parent)continue;
else
{
Multiway_tree*t1n = t1;
while (t1n->brother)t1n = t1n->brother;
Multiway_tree*t2n = t2;
while (t2n->brother)t2n = t2n->brother;
if (!
((t1->positon >= (t2n->positon + namenum[t2n->num])) || (t2->positon >= (t1n->positon + namenum[t1n->num])))
)
{
int d = 0;
abs(t1->parent->child->positon - t2n->positon - namenum[t2n->num]) > abs(t2->parent->child->positon - t1n->positon - namenum[t1n->num])
? abs(t2->parent->child->positon - t1n->positon - namenum[t1n->num]) : abs(t1->parent->child->positon - t2n->positon - namenum[t2n->num]);
Multiway_tree*t1p = t1, *t2p = t2;
while (t1p->parent != t2p->parent)
{
t1p = t1p->parent; t2p = t2p->parent;
}
int n = 0;
Multiway_tree*temp = t1p;
for (temp = t1p, n = 0; temp != t2p && temp; temp = temp->brother)
++n;
if (temp != t2p)
{
for (temp = t2p, n = 0; temp != t1p && temp; temp = temp->brother)
++n;
d = abs(t1->parent->child->positon - t2n->positon - namenum[t2n->num]);
}
else {
d = abs(t2->parent->child->positon - t1n->positon - namenum[t1n->num]);
}
//4???
int averaged = (d + distance) / n + 1;
if (t1p->parent->childrennum % 2 == 0)
{
int childn = 0;
temp = t1p->parent->child;
while (temp)
{
childn++;
int t = averaged*(childn - t1p->parent->childrennum / 2) - averaged / 2;
positionadd(temp, t);
temp = temp->brother;
}
}
else
{
int childn = 0;
temp = t1p->parent->child;
while (temp)
{
childn++;
int t = averaged*(childn - (t1p->parent->childrennum + 1) / 2);
positionadd(temp, t);
temp = temp->brother;
}
}
}
}
}
}
}
int minposition = INT_MAX;
pcur = root;
while (pcur || !s.empty())
{
if (pcur)
{
if (minposition > pcur->positon)
minposition = pcur->positon;
s.push(pcur);
pcur = pcur->child;
}
else
{
pcur = s.top();
s.pop();
pcur = pcur->brother;
}
}
positionadd(root, -1 * minposition + 1);
COORD info = GetLargestConsoleWindowSize(GetStdHandle(STD_OUTPUT_HANDLE));
if (root->positon < info.X / 4);
positionadd(root, info.X / 4 - root->positon);
string *output = new string[(gener + 1) * 3];
for (int i = 0; i < (gener + 1) * 3; ++i)
output[i].append(119, ' ');
for (int i = 1; i < gener + 1; ++i)
{
for (Multiway_tree *temp = p1[i]; temp; temp = temp->next)
{
string t = temp->name ;
output[i].replace(temp->positon, namenum[temp->num], t);
output[i + gener].replace(temp->positon + namenum[temp->num] / 2, 1, (temp->positionmark));
output[i + gener * 2].replace(temp->positon + namenum[temp->num] / 2, to_string(temp->num).size(), to_string(temp->num));
}
}
for (int i = 1; i < gener + 1; ++i)
{
cout << output[i + gener * 2] << endl << output[i] << endl << endl;
if (i != gener)cout << output[i + 1 + gener] << endl << endl;
}
}
下载地址
https://download.csdn.net/download/li_haoren/10336965
perorder.txt inorder.txt 分别是对本质的二叉树的前序和中序遍历保存的文件


 浙公网安备 33010602011771号
浙公网安备 33010602011771号