平面分割类问题

一．      n条直线分割平面

l  问题描述：n条直线，最多可以把一个平面分为多少个区域。

l  公式：f(n)=f(n-1)+n=n(n+1)/2+1;

l  分析：当有n-1条直线时，平面最多被分割成 f(n-1) 个区域。则第n条直线要切成的区域数最多，就必须于每条直线相交且不能有同一交点。这样就会得到(n-1)个交点。这些交点将第n条直线分为2条射线和n-2条线段。而每条射线 和断线将已有的区域一分为二。这样就多出了2+（n+2）个区域。

 

二．      n条折线分割平面

l  问题描述：n条折线，最多可以把一个平面分割为多少个区域，如图所示：

 

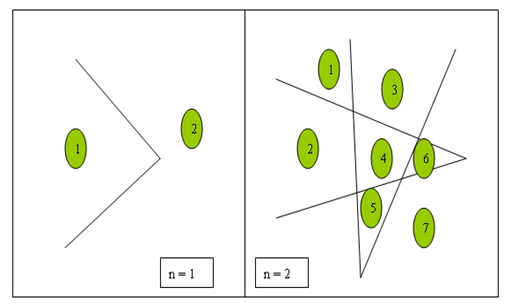
l  公式：f(n)=f(n-1)*4(n-1)+2-1=2*n^2-n+1;

l  分析：根据直线分割平面可知，由交点决定了射线和线段的条数，进而决定了新增的区域数。当（n-1）条折线时，区域数值为f(n-1)。为了使新增的区域最多，则折线的两边的线段要和（n-1）条折线的边，即2*(n-1)条线段相交。那么新增的线段数为4*(n-1)，射线数为2。但要注意的使，折线本身相邻的两线段只能增加一个区域。

 

一．      封闭曲线分割平面

l  问题描述：有n条封闭曲线画在平面上，而任何两条封闭曲线恰好相交于两点，且任何三条封闭曲线不相交于同一点。问这些封闭曲线把平面分割成的区域个数。

l  公式：f(n)=f(n-1)+2(n-1)=n^2-n+1;

l  分析：当(n-1)个圆时，区域数为f(n-1)，那么第n个圆就必须与前(n-1)个圆相交，则第n个圆被分为2(n-1)线段，增加了2*(n-1)个区域。

 

二．      平面分割问题

l  问题描述：n个二维平面，最多可以把一个三位空间分割成多少个区域。

l  公式：f(n)=f(n-1)+g(n-1)=(n^3+5*n)/6+1   ps: g(n)=n(n+1)/2+1;

l  分析：由二维的分割问题可知，平面分割与线之间的交点有关，即交点决定射线和线段的条数，从而决定新增的区域数。试想在三维中则是否与平面的交线有关呢？当有n-1个平面时，分割的空间数为f（n-1）。要有最多的空间数，则第n个平面需与前n-1个平面相交，且不能有共同的交线。即最多有n-1 条交线。而这n-1条交线把第n个平面最多分割成g（n-1）个区域。（g（n）为（1）中的直线分平面的个数）此平面将原有的空间一分为二，则最多增加g（n-1）个空间。

原版博客：http://www.cnblogs.com/chaosheng/archive/2012/01/26/2329583.html