一、递归概念
先看一个例子：
你坐在电影院看电影，你想知道自己是第几排，但是太黑了，数不清，只能问你的前一排是第几排，你就是你的前一排加1，
但前一排也不知道自己是第几排，只能再问他的前一排，，，
问到第一排的时候，第一排告诉第二排自己是第一排，
第二排知道自己是第二排了，
第二排再告诉第三排，第三排知道自己是第三排了，
第三排再告诉第四排，，，
传到你，你就知道自己是第几排了。
所以递归是什么？
递归就是一个程序或函数在其中定义或说明有之间或者间接调用自身的一种方法，它通常把一个大型复杂的问题层层转化为一个原问题相似的规模较小的问题来求解。
递归策略只需要少量的程序就可以描述出解题过程所需要的多次重复计算，大大的减少了程序的代码量。
递归的能力在于用有限的语句来定义对象的无限集合，一般来说，递归需要边界条件，递归前进段和递归返回段，当边界条件不满足时，递归前进，当边界条件满足时，递归返回。
二、案例
1、阶乘
例如4的阶乘是1*2*3*4，递归算法计算过程就是4*3*2*1
package main
func main() {
fmt.Println(jiecheng(4))
}
//阶乘
func jiecheng(n int) int{
if(n == 1) {
return 1
}
return n * jiecheng(n-1)
}
2、斐波那契数列
斐波纳契数列，又称黄金分割数列，指的是这样一个数列：1、1、2、3、5、8、13、21、……
这个数列从第三项开始，每一项都等于前两项之和。
延伸出有趣的兔子实际问题：
一般而言，兔子在出生两个月后，就有繁殖能力，一对兔子每个月能生出一对小兔子来。如果所有兔子都不死，那么一年以后可以繁殖多少对兔子？
分析如下：
原始兔子，1对：
第1个月：小兔子没有繁殖能力，所以还是1对；
第2个月，生下1对小兔子，总数共有2对；
第3个月，1月份的兔子生下1对小兔子，加上2月的兔子数，共2对，也就是1月+2月=3月的兔子数量
第4个月，2月份的兔子生下2对小兔子，加上3月的兔子数，共5对，也就是2月+3月=4月的兔子数量
以此类推.......
从第3个月开始，每个月的兔子数是上上个月加上个月的兔子之和。
package main
func main() {
for i := 0;i<10; i++ {
fmt.Print(febonacci(i)," ")
}
}
//斐波那契数列
func febonacci(n int) int{
if(n<2){
return n
}
return febonacci(n-2) + febonacci(n-1)
}
3、二分查找
首先二维数组一定是有序的，
在有序的数组array[]中，不断地将中间值（mid）和被查找的值比较，
如果被查找的值等于affay[],就返回下标array[mid]，否则就像查找的范围缩小一半，
如果被查找的小于array【mid】,就继续查找左边的值，
如果查找大于array【mid】就向右边查找，
直到查找为空,查找结束!
代码如下：
package main
func main() {
arr := [...]int{1,2,3,4,5,6}
fmt.Println(search(0,len(arr)-1,arr,6))
}
//二分查找
func search(start int,end int,arr [6]int,n int) int{
m := end-start
mid := start + m / 2
//如果起始与结束下标相同，并且该下标的值与查找的值n相同，则直接返回该下标
if m == 0 && arr[start] == n {
return start
} else if m < 0 {
//特殊情况，未找到n的下标，直接返回-1
return -1
} else {
//中间值与查找的值n相同，返回中间值的下标
if(arr[mid] == n){
return mid
}else if(arr[mid] < n) {
// n大于中间值，说明要查找的n值在右半部分，递归查找右半部分
return search(mid+1,end,arr,n)
}else {
// n小于中间值，说明要查找的n值在左半部分，递归查找左半部分
return search(start,mid-1,arr,n)
}
}
}
4、汉诺塔问题
汉诺塔问题是由很多放置在三个塔座上的盘子组成的一个古老的难题，如下图所示，所有的盘子的直径是不同的。并且盘子中央都有一个洞使得它刚好可以放在塔座上，所有的盘子刚开始都是在a座上，这个难题的目标是将左右的盘子都从塔座a，移到塔座c上，每次只可以移动一个盘子，并且任何一个盘子都不可以放置在比它小的盘子上。
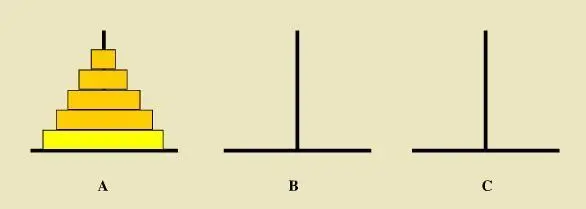
这个问题可以先从简单的方面想，然后一步一步出发，
假设有2个盘子，盘子的大小我按照阿拉伯数字从小到大命名为1、2。
如果a上面有两个盘子，分别是1,2，那么我们只需要把1的盘子移到b上面，然后把2的盘子移到c上面，最后把b上面的盘子1移动到c上面就可以了，这样两个盘子的问题就解决了。
如果是三个盘子呢？
我们一样的来命名1,2,3，假设先把1的盘子移动到c的上面，然后把2的盘子移动到b上面，这样目前就是a上面的是3，b上面的是2，c上面的是1，然后将c上面的盘子移动到b上面，继续把a的盘子移动到c上面，这样的话，目前就是b上面有1,2，c上面的有3，现在答案已经很清楚了，将b上面的盘子移动到a上面，然后第二个盘子移动到c上面，最后a的盘子移动到c上面，这样问题就解决了，
但是如果有四个，五个，n个盘子呢？
这个时候递归的思想就很好的解决这样的问题了，当只有两个盘子的时候，我们只需要将b塔座作为中介，将盘子1放到中介b上面，然后将盘子2放到c上面，最后将b上面的盘子1移动到c盘就可以了
所以无论多少盘子，我们都将其看做只有两个盘子，假设n个盘子在a的上面，我们将其看做只有两个盘子，只有（n-1）和n这两个盘子
先将a上面的n-1的哪一个盘子放到塔座b上面，然后将第n的盘子放到目标塔上面，
然后a的上面为空，看做中间塔，b上面的有n-1个盘子，将第n-2以下的盘子看成一个盘子，放到中间a塔上面，然后将第n-1的盘子放到c上面，
这是发现a上面有n-2个盘子，b上面为空，按照上面的方式以此类推，直到全部放到冰箱里面
简单的来说：
从初始塔a上移动到包含n-1个盘子到c上面
将a上面剩下的一个盘子，放到c上面
然后假设b上面有n-1个盘子，然后将它看成为n继续将看成n的盘子中间的n-1个盘子放到a上面
将b上面剩下的那个盘子放到c上面。
…
package main
func main() {
hannuota(3,"A","B","C")
}
//汉诺塔问题
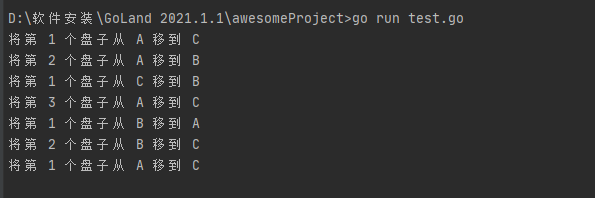
func hannuota(n int,from string,temp string,to string) {
//就剩一个盘子的，直接将这个盘子从起始盘移到目标盘
if n == 1 {
fmt.Println("将第",n,"个盘子从",from,"移到",to)
}else{
//将上面的n-1个盘子从起始盘移到中转盘
hannuota(n-1,from,to,temp)
//将最下面的第n个盘子从起始盘移到目标盘
fmt.Println("将第",n,"个盘子从",from,"移到",to)
//再将中转盘上面的n-1个盘子移到目标盘
hannuota(n-1,temp,from,to)
}
}
参考：https://blog.csdn.net/qq_40688338/article/details/84837816，https://www.cnblogs.com/joinclear/archive/2013/02/06/2908247.html
初入职场热爱分享的打工人一枚，请大家多多指教~~
