动态规划的概念对于新手来说枯燥难懂,就算看懂了,做题的时候依旧抓耳挠腮的毫无头绪,这些比较难理解的算法,还是需要根据例子来一步步学习和理解,从而熟练掌握,下面,咱们就通过一个简单的小例子来学习动态规划:
数字三角形(POJ1163)
在上面的数字三角形中寻找一条从顶部到底边的路径,使得路径上所经过的数字之和最大。
路径上的每一步都只能往左下或 右下走。只需要求出这个最大和即可,不必给出具体路径。 三角形的行数大于1小于等于100,数字为 0 - 99
输入格式:
5 //表示三角形的行数 接下来输入三角形
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
要求输出最大和
咱们来分析这道题:
1.需要有一个变量 n 来存储输入的行数


2.需要一个二维数组 a 来存储输入的数字三角形
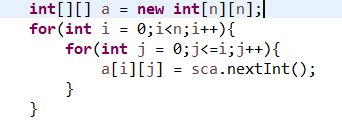
3.需要另一个同样大小的二维数组 b,用来存储到每一层的每一个数的最短路径,
例如:
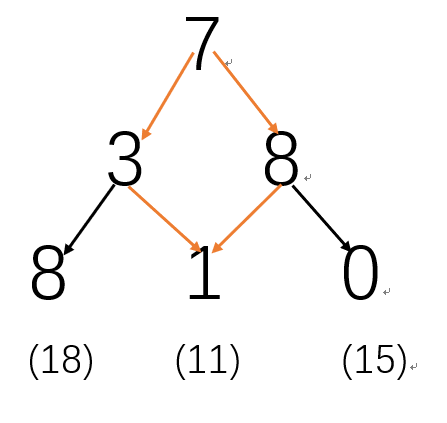
到三角形的第三层,有两条路会经过1,
由于7+3=10<7+8=15,所以b数组的1的位置存储的是最短路径7—>3—>1等于11,
而在最两边的,就直接累加就ok了,7+3+8=18,7+8+0=15
这也是这个程序的核心部分,代码如下:
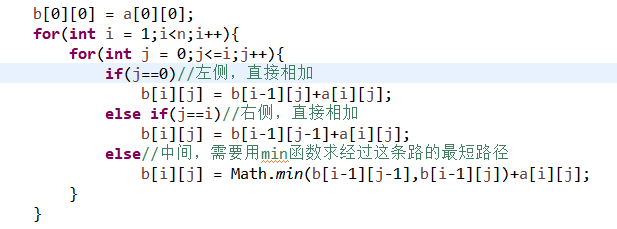
因为第一层跟a数组的第一层相同,所以i从1开始循环
然后遍历最后一层,求出最小值就ok啦

b数组最后的值
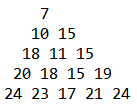
完整代码如下:
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
Scanner sca = new Scanner(System.in);
int n = sca.nextInt();
int[][] a = new int[n][n];
int[][] b = new int[n][n];
int min;
for(int i = 0;i<n;i++){
for(int j = 0;j<=i;j++){
a[i][j] = sca.nextInt();
}
}
b[0][0] = a[0][0];
for(int i = 1;i<n;i++){
for(int j = 0;j<=i;j++){
if(j==0)//左侧,直接相加
b[i][j] = b[i-1][j]+a[i][j];
else if(j==i)//右侧,直接相加
b[i][j] = b[i-1][j-1]+a[i][j];
else//中间,需要用min函数求经过这条路的最短路径
b[i][j] = Math.min(b[i-1][j-1],b[i-1][j])+a[i][j];
}
}
min = b[n-1][0];
for(int i = 1;i<b[n-1].length;i++){
if(b[n-1][i]<min)
min = b[n-1][i];
}
System.out.println(min);
}
}
总结一下动态规划的解题思路:
1,将原问题分解为简单的子问题,子问题求出来之后,原问题也就很容易得到了
2,确定状态转移方程
这道题的状态转移方程:
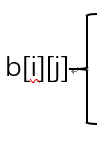

动态规划一般可分为线性动规,区域动规,树形动规,背包动规四类。
举例:
线性动规:拦截导弹,合唱队形,挖地雷,建学校,剑客决斗等;
区域动规:石子合并, 加分二叉树,统计单词个数,炮兵布阵等;
树形动规:贪吃的九头龙,二分查找树,聚会的欢乐,数字三角形等;
背包问题:01背包问题,完全背包问题,分组背包问题,二维背包,装箱问题,挤牛奶(同济ACM第1132题)等;
应用实例:
以上例子,每类挑选一题或两题练习即可
所有的算法都需要多加练习,应用起来才能得心应手,希望我的这篇博客能给各位爱学习的同伴们带去一些收获,我也是新手,大家共同努力,加油!

