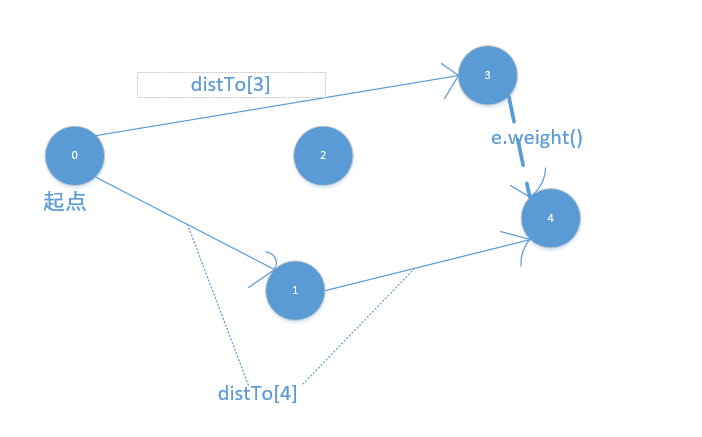
松弛操作
Dijkstra算法和BellmanFord算法都是基于这个简单的操作。
下面我们来了解这个简单而重要的操作:
- 线松弛
线松弛也就是处理
起点到边的两个顶点距离与两个顶点直接距离的问题。
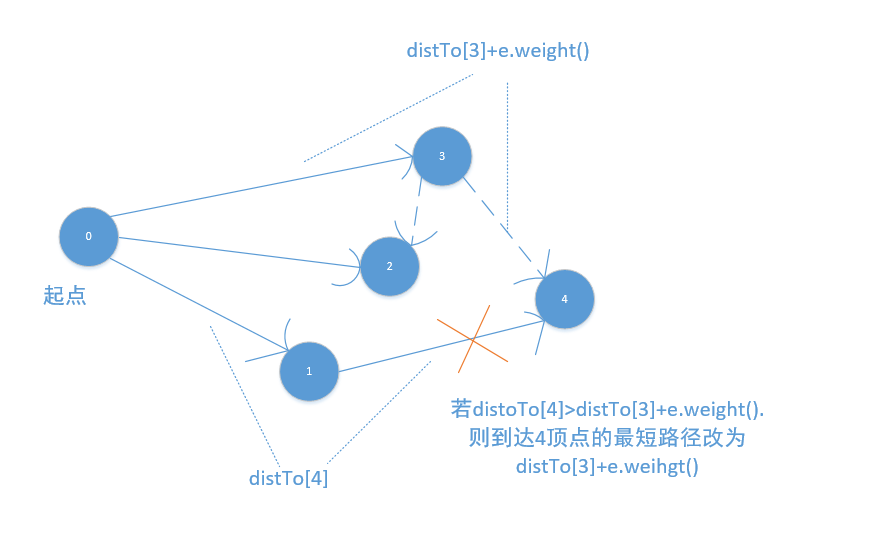
如:假如distTo[4]>distTo[3]+e.weight(),则会修改到达4顶点的最短路径,否则不变。
2.点松弛
点松弛其实就是对顶点的每一条发出的边都进行一次线松弛操作。
如图:边3->2,同样要进行线松弛。
Dijkstra算法
直接附上代码了(有详细解释)
性能:任何情况下都能保证较好的性能(当然,此算法不能存在负值的边)
package ShortestPath;
import java.util.Stack;
/**
*基于解决加非负权值有向图的单起点的最短路径问题Dijkstra算法
*该类维护了三个变量:{@link DirectedEdge}类数组{@link path};{@link double}数组{@link distTo};{@link IndexMinPQ}优先队列{@link pq}
*<p>其中path保存了到达某个顶点的最短路径;distTo[w]:起点到w的权值和(初始都为0,起点除外);pq:保存了顶点的优先队列
*<p>算法思想:每次都为最短路径增加一条边,直至涵盖所有的顶点或者非树顶点的distTo都为无穷大的时候结束。
* @author 罗正
* @date 2016年9月23日 上午9:41:42
**/
public class DijkstraSP {
private IndexMinPQ<Double> pq; //顶点的优先队列
private double[] distTo; //每个顶点的距离(初始化为无穷大)
private DirectedEdge[] path; //保存了关键路径的边
/**
* 构造的Dijkstra函数,传入带权值无向图g,以及起点s
* */
public DijkstraSP(EdgeDigraph g,int s)
{
//初始化
distTo = new double[g.V()];
pq = new IndexMinPQ<Double>(g.V());
path = new DirectedEdge[g.V()];
//将所有顶点与起点的距离都初始化为无穷大
for(int v = 0;v<g.V();v++)
distTo[v] = Double.POSITIVE_INFINITY;
//将起点距离设置为0,并加入到优先队列中
distTo[s] = 0.0;
pq.insert(s, 0.0);
while(!pq.isEmpty())
{
relax(g,pq.delMin());
}
}
/**
* 最短路径的关键方法:边的松弛(relaxation)
* <p>该方法会维护所有v到达的边(即以v为起点的边),假设存在v->w(非树):
* 首先方法会循环到v->w这条边;
* <p>假若:起点到w的距离(distTo[w])比起点到达v的距离(distTo[v])和v->w的边((v->w).weight())还要大的话;
* <p>那么是不是对于求最短路径来说,到达w顶点的路径是不是就要变成先到达v再由v到达w呢,这是显然的。
* @param g
* @param v
*/
private void relax(EdgeDigraph g,int v)
{
for(DirectedEdge e : g.adj(v))
{
int w = e.to();
if(distTo[w]>distTo[v]+e.weight())
{
distTo[w] = distTo[v]+e.weight();
path[w] = e;
/*假如w已经包含在最短路径中,也还是要修改到达w的路径的,因为已经更短了啊*/
if(pq.contains(w))
pq.change(w, distTo[w]);
else
pq.insert(w, distTo[w]);
}
}
}
public double distto(int v)
{
return distTo[v];
}
public boolean hasPath(int v)
{
return distTo[v]<Double.POSITIVE_INFINITY;
}
public Iterable<DirectedEdge> path(int v)
{
if(!hasPath(v))
return null;
else
{
Stack<DirectedEdge> pathTo = new Stack<>();
for(DirectedEdge e = path[v];e != null; e = path[e.from()])
pathTo.push(e);
return pathTo;
}
}
public static void main(String[] args) {
DirectedEdge e1 = new DirectedEdge(0, 1, 100);
DirectedEdge e2 = new DirectedEdge(1, 3, 200);
DirectedEdge e3 = new DirectedEdge(0, 2, 200);
DirectedEdge e4 = new DirectedEdge(2, 3, 200);
EdgeDigraph g = new EdgeDigraph(4);
g.addEdge(e1);
g.addEdge(e2);
g.addEdge(e3);
g.addEdge(e4);
DijkstraSP dij = new DijkstraSP(g, 0);
System.out.println(dij.path(3));
}
}
Bellman—Ford 算法
这里讨论的是基于队列的BellmanFord算法的实现。
此算法适用于任何情况(当然,存在负权值环对于求最短路径是没有意义的。)
package ShortestPath;
import java.util.ArrayDeque;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
import minSpanningTree.Edge;
/**
*基于队列的Bellman-Ford算法: 将起点的distTo[s]初始为0,将其他所有顶点distTo初始为无穷大,任意顺序放松所有边,重复V轮。
*<p>思路:与Dijkstra算法类似,double数组distTo意义一样;
*队列queue保存放松的顶点;不同的是增加一个标记标记重复每轮放松的顶点和下一轮放松的顶点(使得队列不会重复保存顶点),下轮在放松函数里设置为true,以便保证下轮不重复;
*Bellman—Ford算法对于一般加权值图,其中就包括了负值权值(但是假若存在负权值的环,则对于求最短路径则没有意义了)
*<p>1>首先明白为什么存在负权值换对于求最短路径没有意义?因为在环里每重复一次,我们都能得到一条更短的路径。
*<p>2>加入存在负权值环,relax过程会有什么异常呢?由上一个问题答案,我们知道,这个过程假如和Dijstra算法无异,则会无限循环下去
*<p>3>如何确定存在负权值环呢?我们前面已经知道,重复V轮,我们就能得到最短路径,
*事实上我们只需要V-1轮结束后,就能得到最短路径,所以,假如重复了V轮,是不是就说明存在负权值环了呢
*
* @author 罗正
* @date 2016年9月23日 下午3:40:23
**/
public class BellmanFordSP {
private double[] distTo;
private boolean[] onQ;
private DirectedEdge[] edgeTo;
private Queue<Integer> queue;
//对于检测负权值环定义的变量
private int count;
private Iterable<DirectedEdge> cycle;
/**
* 此函数和Dijkstra算法的函数并无太大区别,只是增加了onQ[],标记顶点。
* @param g
* @param s
*/
public BellmanFordSP(EdgeDigraph g,int s)
{
distTo = new double[g.V()];
onQ = new boolean[g.V()];
int count = 0;
queue = new ArrayDeque<>();
edgeTo = new DirectedEdge[g.V()];
for(int i = 0;i<g.V();i++)
distTo[i] = Double.POSITIVE_INFINITY;
distTo[s] = 0.0;
onQ[s] = true;
queue.add(s);
while(!queue.isEmpty())
{
int v = queue.remove();
onQ[v] = false;
relax(g,v);
}
}
/*放松操作*/
private void relax(EdgeDigraph g,int v)
{
for(DirectedEdge e : g.adj(v))
{
int w = e.to();
if(distTo[w] > distTo[v]+e.weight())
{
distTo[w] = distTo[v]+e.weight();
edgeTo[w] = e;
if(!onQ[w])
{
queue.add(w);
onQ[w] = true;
}
}
//假如存在环,则count == V
if(count++ % g.V() == 0)
findNegativeCycle();
}
}
public double distto(int v)
{
return distTo[v];
}
public boolean hasPath(int v)
{
return distTo[v]<Double.POSITIVE_INFINITY;
}
public Iterable<DirectedEdge> path(int v)
{
if(!hasPath(v))
return null;
else
{
Stack<DirectedEdge> pathTo = new Stack<>();
for(DirectedEdge e = edgeTo[v];e != null; e = edgeTo[e.from()])
pathTo.push(e);
return pathTo;
}
}
//检测环函数,并保存环
private void findNegativeCycle()
{
int V = edgeTo.length;
EdgeDigraph g;
g = new EdgeDigraph(V);
for(int v = 0;v<V;v++)
{
if(edgeTo[v] != null)
g.addEdge(edgeTo[v]);
}
EdgeWeightedDirectedCycle c = new EdgeWeightedDirectedCycle(g);
cycle = c.cycle();
}
public boolean hasNegativeCycle()
{
return cycle == null;
}
public Iterable<DirectedEdge> negativeCycle()
{
return cycle;
}
}