Java 内功修炼 之 数据结构与算法(一)
一、基本认识
1、数据结构与算法的关系?
(1)数据结构(data structure):
数据结构指的是 数据与数据 之间的结构关系。比如:数组、队列、哈希、树 等结构。
(2)算法:
算法指的是 解决问题的步骤。
(3)两者关系:
程序 = 数据结构 + 算法。
解决问题可以有很多种方式,不同的算法实现 会得到不同的结果。正确的数据结构 是 好算法的基础(算法好坏取决于 如何利用合适的数据结构去 处理数据、解决问题)。
(4)数据结构动态演示地址:
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
2、数据结构分类?
(1)分类:
数据结构 可以分为 两种:线性数据结构、非线性数据结构。
(2)线性数据结构:
线性数据结构指的是 数据元素之间存在一对一的线性关系。比如:一维数组、链表、队列、栈。
其又可以分为:
顺序存储结构:指的是 使用一组地址连续的存储单元 存储数据元素 的结构,其每个元素节点仅用于 保存数据元素。比如:一维数组。
链式存储结构:指的是 可使用一组地址不连续的存储单元 存储数据元素 的结构,其每个元素节点 保存数据元素 以及 相邻数据元素的地址 信息。比如:链表。
(3)非线性数据结构:
非线性数据结构指的是 数据元素之间存在 一对多、多对多 的关系。比如:二维数组、多维数组、树、图 等。
3、时间复杂度、空间复杂度
(1)分析多个算法执行时间:
事前估算时间:程序运行前,通过分析某个算法的时间复杂度来判断算法解决问题是否合适。
事后统计时间:程序运行后,通过计算程序运行时间来判断(容易被计算机硬件、软件等影响)。
注:
一般分析算法都是采用 事前估算时间,即估算分析 算法的 时间复杂度。
(2)时间频度、时间复杂度:
时间频度( T(n) ):
一个算法中 语句执行的次数 称为 语句频度 或者 时间频度,记为 T(n)。
通常 一个算法花费的时间 与 算法中 语句的执行次数 成正比,即 某算法语句执行次数多,其花费时间就长。
时间复杂度( O(f(n)) ):
存在某个辅助函数 f(n),当 n 接近无穷大时,若 T(n) / f(n) 的极限值为不等于零的常数,则称 f(n) 为 T(n) 的同数量级函数,记为 T(n) = O(f(n)),称 O(f(n)) 为算法的渐进时间复杂度,简称 时间复杂度。
(3)通过 时间频度( T(n) )推算 时间复杂度 ( O(f(n)) ):
对于一个 T(n) 表达式,比如: T(n) = an^2 + bn + c,其推算为 O(n) 需要遵循以下规则:
rule1:使用常数 1 替代表达式中的常数,若表达式存在高阶项,则忽略常数项。
即:若 T(n) = 8,则其时间复杂度为 O(1)。若 T(n) = n^2 + 8,则其时间复杂度为 O(n^2)。
rule2:只保留最高阶项,忽略所有低次项。
即:T(n) = 3n^2 + n^4 + 3n,其时间复杂度为 O(n^4)。
rule3:去除最高阶项的系数。
即:T(n) = 3n^2 + 4n^3,其时间复杂度为 O(n^3)。
注:
T(n) 表达式不同,但是其对应的时间复杂度可能相同。
比如:T(n) = n^2 + n 与 T(n) = 3n^2 + 1 的时间复杂度均为 O(n^2)。
(4)常见时间复杂度
【常见时间复杂度(由小到大排序如下):】 O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(n^k) < O(2^n) 注: 时间复杂度越大,算法执行效率越低。 【常数阶 O(1) :】 算法复杂度 与 问题规模无关。 比如: int a = 1; int b = 2; int c = a + b; 分析: 代码中不存在循环、递归等结构,其时间复杂度即为 O(1)。 【对数阶 O(logn) :】 算法复杂度 与 问题规模成对数关系。 比如: int i = 1; while(i < n) { i*=2; // 不断乘 2 } 分析: 上述代码中存在循环,设循环执行次数为 x,则循环退出条件为 2^x >= n。 从而推算出 x = logn,此时 log 以 2 为底,即时间复杂度为 O(logn)。 【线性阶 O(n) :】 算法复杂度 与 问题规模成线性关系。 比如: for(int i = 0; i < n; i++) { System.out.println(i); } 分析: 代码中存在循环,且循环次数为 n,即时间频度为 T(n),从而时间复杂度为 O(n)。 【线性对数阶 O(nlogn) :】 算法复杂度 与 问题规模成线性对数关系(循环嵌套)。 比如: for(int j = 0; j < n; j++) { int i = 1; while(i < n) { i*=2; // 不断乘 2 } } 分析: 代码中循环嵌套,完成 for 循环需要执行 n 次,每次均执行 while 循环 logn 次, 即总时间频度为 T(nlogn), 从而时间复杂度为 O(nlogn)。 【平方阶 O(n^2) :】 算法复杂度 与 问题规模成平方关系(循环嵌套)。 比如: for(int i = 0; i < n; i++) { for(int j = 0; j < n; j++) { System.out.println(i + j); } } 分析: 代码中循环嵌套,总时间频度为 T(n*n),即时间复杂度为 O(n^2) 【立方阶 O(n^3) 、k 次方阶 O(n^k) :】 类似于平方阶 O(n^2),只是循环嵌套的层数更多了。 O(n^3) 表示三层循环。O(n^K) 表示四层循环。 【指数阶 O(2^n) :】 算法复杂度 与 问题规模成指数关系(循环嵌套)。 这个算法的执行效率非常糟糕,一般都不考虑。 比如: int n = 3; for (int i = 0; i < Math.pow(2, n); i++) { System.out.println(i); } 分析: 上面循环,总时间频度为 T(2^n),即时间复杂度为 O(2^n)。
(5)空间复杂度
空间复杂度 指的是算法所需耗费的存储空间。与时间复杂度类似,但其关注的是算法执行所需占用的临时空间(非语句执行次数)。
一般算法分析更看重 时间复杂度,即保证程序执行速度快,比如:缓存 就是空间换时间。
二、基本数据结构以及代码实现
1、稀疏数组(Sparse Array)
(1)什么是稀疏数组?
当数组中 值为 0 的元素 大于 非 0 元素 且 非 0 元素 分布无规律时,可以使用 稀疏数组 来表示该数组,其将一个大数组整理、压缩成一个小数组,用于节约磁盘空间。
注:
不一定必须为 值为 0 的元素,一般 同一元素在数组中过多时即可。
使用 稀疏数组 的目的是为了 压缩数组结构、节约磁盘空间(比如:一个二维数组 a[10][10] 可以存储 100 个元素,但是其只存储了 3 个元素后,那么将会有 97 个空间被闲置,此时可以将 二维数组 转为 稀疏数组 存储,其最终转换成 b[4][3] 数组进行保存,即从 a[10][10] 的数组 压缩到 b[4][3],从而减少空间浪费)。
【举例:】 定义二维数组 a[4][5],并存储 3 个值如下: 0 0 0 0 0 0 1 0 2 0 0 0 0 0 0 0 0 1 0 0 此时,数组中元素为 0 的个数大于 非 0 元素个数,所以可以作为 稀疏数组 处理。 换种方式,比如 将 0 替换成 5 如下,也可以视为 稀疏数组 处理。 5 5 5 5 5 5 1 5 2 5 5 5 5 5 5 5 5 1 5 5
(2)二维数组转为稀疏数组:
【如何处理:】 Step1:先记录数组 有几行几列,有多少个不同的值。 Step2:将不同的值 的元素 的 行、列、值 记录在一个 小规模的 数组中,从而将 大数组 缩减成 小数组。 【举例:】 原二维数组如下: 0 0 0 0 0 0 1 0 2 0 0 0 0 0 0 0 0 1 0 0 经过处理后变为 稀疏数组 如下: 行 列 值 4 5 3 // 首先记录原二维数组 有 几行、几列、几个不同值 1 1 1 // 表示原二维数组中 a[1][1] = 1 1 3 2 // 表示原二维数组中 a[1][3] = 2 3 2 1 // 表示原二维数组中 a[3][2] = 1 可以看到,原二维数组 a[4][5] 转为 稀疏数组 b[4][3],空间得到利用、压缩。
(3)二维数组、稀疏数组 互相转换实现
【二维数组 转 稀疏数组:】 Step1:遍历原始二维数组,得到 有效数据 个数 num。 Step2:根据有效数据个数创建 稀疏数组 a[num + 1][3]。 Step3:将原二维数组中有效数据存储到 稀疏数组中。 注: 稀疏数组有 三列:分别为:行、 列、 值。 稀疏数组 第一行 存储的为 原二维数组的行、列 以及 有效数据个数。其余行存储 有效数据所在的 行、列、值。 所以数组定义为 [num + 1][3] 【稀疏数组 转 二维数组:】 Step1:读取 稀疏数组 第一行数据并创建 二维数组 b[行][列]。 Step2:读取其余行,并赋值到新的二维数组中。 【代码实现:】 package com.lyh.array; import java.util.HashMap; import java.util.Map; public class SparseArray { public static void main(String[] args) { // 创建原始 二维数组,定义为 4 行 10 列,并存储 两个 元素。 int[][] arrays = new int[4][10]; arrays[1][5] = 8; arrays[2][3] = 7; // 遍历输出原始 二维数组 System.out.println("原始二维数组如下:"); showArray(arrays); // 二维数组 转 稀疏数组 System.out.println("\n二维数组 转 稀疏数组如下:"); int[][] sparseArray = arrayToSparseArray(arrays); showArray(sparseArray); // 稀疏数组 再次 转为 二维数组 System.out.println("\n稀疏数组 转 二维数组如下:"); int[][] sparseToArray = sparseToArray(sparseArray); showArray(sparseToArray); } /** * 二维数组 转 稀疏数组 * @param arrays 二维数组 * @return 稀疏数组 */ public static int[][] arrayToSparseArray(int[][] arrays) { // count 用于记录有效数据个数 int count = 0; // HashMap 用于保存有效数据(把 行,列 用逗号分隔拼接作为 key,值作为 value) Map<String, Integer> map = new HashMap<>(); // 遍历得到有效数据、以及总个数 for (int i = 0; i < arrays.length; i++) { for (int j = 0; j < arrays[i].length; j++) { if (arrays[i][j] != 0) { count++; map.put(i + "," + j, arrays[i][j]); } } } // 根据有效数据总个数定义 稀疏数组,并赋值 int[][] result = new int[count + 1][3]; result[0][0] = arrays.length; result[0][1] = arrays[0].length; result[0][2] = count; // 把有效数据从 HashMap 中取出 并放到 稀疏数组中 for(Map.Entry<String, Integer> entry : map.entrySet()) { String[] temp = entry.getKey().split(","); result[count][0] = Integer.valueOf(temp[0]); result[count][1] = Integer.valueOf(temp[1]); result[count][2] = entry.getValue(); --count; } return result; } /** * 遍历输出 二维数组 * @param arrays 二维数组 */ public static void showArray(int[][] arrays) { for (int[] a : arrays) { for (int data : a) { System.out.print(data + " "); } System.out.println(); } } /** * 稀疏数组 转 二维数组 * @param arrays 稀疏数组 * @return 二维数组 */ public static int[][] sparseToArray(int[][] arrays) { int[][] result = new int[arrays[0][0]][arrays[0][1]]; for (int i = 1; i < arrays.length; i++) { result[arrays[i][0]][arrays[i][1]] = arrays[i][2]; } return result; } } 【输出结果:】 原始二维数组如下: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 二维数组 转 稀疏数组如下: 4 10 2 1 5 8 2 3 7 稀疏数组 转 二维数组如下: 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 8 0 0 0 0 0 0 0 7 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
2、队列(Queue)、环形队列
(1)什么是队列?
队列指的是一种 受限的、线性的数据结构,其仅允许在 一端进行插入操作(队尾插入,rear),且在另一端进行 删除操作(队首删除,front)。
队列可以使用 数组 或者 链表 实现(一般采用数组实现,仅在首尾增删,效率比链表高)。
其遵循 先进先出(First In First Out,FIFO) 原则,即先存入 队列的值 先取出。
【使用 数组实现 队列:】 需要注意三个值: maxSize: 表示队列最大容量。 front: 表示队列头元素下标(指向队列头部的第一个元素的前一个位置),初始值为 -1. rear: 表示队列尾元素下标(指向队列尾部的最后一个元素),初始值为 -1。 临界条件: front == rear 时,表示队列为 空。 rear == maxSize - 1 时,表示队列已满。 rear - front, 表示队列的存储元素的个数。 数据进入队列时: front 不动,rear++。 数据出队列时: rear 不动,front++。
如下图:
红色表示入队操作,rear 加 1。
黄色表示出队操作,front 加 1。
每次入队,向当前实际数组尾部添加元素,每次出队,从当前实际数组头部取出元素,符合 先进先出原则。

可以很明显的看到,如果按照这种方式实现队列,黄色区域的空间将不会被再次使用,即此时的队列是一次性的。
那么如何重复利用 黄色区域的空间?可以采用 环形队列实现(看成一个环来实现)。
环形队列在 上面队列的基础上稍作修改,当成环处理(数据首尾相连,可以通过 % 进行取模运算实现),核心是考虑 队列 什么时候为空,什么时候为满。
一般采用 牺牲一个 数组空间 作为判断当前队列是否已满的条件。
【使用 数组 实现环形队列:(此处仅供参考)】 需要注意三个值: maxSize: 表示队列最大容量。 front: 表示队列头元素下标(指向队列头部的第一个元素),初始值为 0。 rear: 表示队列尾元素下标(指向队列尾部的最后一个元素的后一个位置),初始值为 0。 临界条件: front == rear 时,表示队列为 空。 (rear + 1) % maxSize == front 时,表示队列已满。 (rear - front + maxSize) % maxSize, 表示队列的存储元素的个数。 数据进入队列时: front 不动,rear = (rear + 1) % maxSize。 数据出队列时: rear 不动,front = (front + 1) % maxSize。

(2)使用数组实现队列
【代码实现:】 package com.lyh.queue; public class ArrayQueue<E> { private int maxSize; // 队列最大容量 private int front; // 队列首元素 private int rear; // 队列尾元素 private Object[] queue; // 存储队列 /** * 构造初始队列 * @param maxSize 队列最大容量 */ public ArrayQueue(int maxSize) { this.maxSize = maxSize; queue = new Object[maxSize]; front = -1; rear = -1; } /** * 添加数据进入队列 * @param e 待入数据 */ public void addQueue(E e) { if (isFull()) { System.out.println("队列已满"); return; } // 队列未满时,添加数据,rear 向后移动一位 queue[++rear] = e; } /** * 从队列中取出数据 * @return 待取数据 */ public E getQueue() { if (isEmpty()) { System.out.println("队列已空"); return null; } // 队列不空时,取出数据,front 向后移动一位 return (E)queue[++front]; } /** * 输出当前队列所有元素 */ public void showQueue() { if (isEmpty()) { System.out.println("队列已空"); return; } System.out.print("当前队列存储元素总个数为:" + getSize() + " 当前队列为:"); for(int i = front + 1; i <= rear; i++) { System.out.print(queue[i] + " "); } System.out.println(); } /** * 获取当前队列实际大小 * @return 队列实际存储数据数量 */ public int getSize() { return rear - front; } /** * 判断队列是否为空 * @return true 为空 */ public boolean isEmpty() { return front == rear; } /** * 判断队列是否已满 * @return true 已满 */ public boolean isFull() { return rear == maxSize - 1; } public static void main(String[] args) { // 创建队列 ArrayQueue<Integer> arrayQueue = new ArrayQueue<>(6); // 添加数据 arrayQueue.addQueue(10); arrayQueue.addQueue(8); arrayQueue.addQueue(9); arrayQueue.showQueue(); // 取数据 System.out.println(arrayQueue.getQueue()); System.out.println(arrayQueue.getQueue()); arrayQueue.showQueue(); } } 【输出结果:】 当前队列存储元素总个数为:3 当前队列为:10 8 9 10 8 当前队列存储元素总个数为:1 当前队列为:9
(3)使用数组实现环形队列
【代码实现:】 package com.lyh.queue; public class ArrayCircleQueue<E> { private int maxSize; // 队列最大容量 private int front; // 队列首元素 private int rear; // 队列尾元素 private Object[] queue; // 存储队列 /** * 构造初始队列 * @param maxSize 队列最大容量 */ public ArrayCircleQueue(int maxSize) { this.maxSize = maxSize; queue = new Object[maxSize]; front = 0; rear = 0; } /** * 添加数据进入队列 * @param e 待入数据 */ public void addQueue(E e) { if (isFull()) { System.out.println("队列已满"); return; } // 队列未满时,添加数据,rear 向后移动一位 queue[rear] = e; rear = (rear + 1) % maxSize; } /** * 从队列中取出数据 * @return 待取数据 */ public E getQueue() { if (isEmpty()) { System.out.println("队列已空"); return null; } // 队列不空时,取出数据,front 向后移动一位 E result = (E)queue[front]; front = (front + 1) % maxSize; return result; } /** * 输出当前队列所有元素 */ public void showQueue() { if (isEmpty()) { System.out.println("队列已空"); return; } System.out.print("当前队列存储元素总个数为:" + getSize() + " 当前队列为:"); for(int i = front; i < front + getSize(); i++) { System.out.print(queue[i] + " "); } System.out.println(); } /** * 获取当前队列实际大小 * @return 队列实际存储数据数量 */ public int getSize() { return (rear - front + maxSize) % maxSize; } /** * 判断队列是否为空 * @return true 为空 */ public boolean isEmpty() { return front == rear; } /** * 判断队列是否已满 * @return true 已满 */ public boolean isFull() { return (rear + 1) % maxSize == front; } public static void main(String[] args) { // 创建队列 ArrayCircleQueue<Integer> arrayQueue = new ArrayCircleQueue<>(3); // 添加数据 arrayQueue.addQueue(10); arrayQueue.addQueue(8); arrayQueue.addQueue(9); arrayQueue.showQueue(); // 取数据 System.out.println(arrayQueue.getQueue()); System.out.println(arrayQueue.getQueue()); arrayQueue.showQueue(); } } 【输出结果:】 队列已满 当前队列存储元素总个数为:2 当前队列为:10 8 10 8 队列已空
3、链表(Linked list)-- 单链表 以及 常见笔试题
(1)什么是链表?
链表指的是 物理上非连续、非顺序,但是 逻辑上 有序 的 线性的数据结构。
链表 由 一系列节点 组成,节点之间通过指针相连,每个节点只有一个前驱节点、只有一个后续节点。节点包含两部分:存储数据元素的数据域 (data)、存储下一个节点的指针域 (next)。
可以使用 数组、指针 实现。比如:Java 中 ArrayList 以及 LinkedList。
(2)单链表实现?
单链表 指的是 单向链表,首节点没有前驱节点,尾节点没有后续节点。只能沿着一个方向进行 遍历、获取数据的操作(即某个节点无法获取上一个节点的数据)。
可参考:https://www.cnblogs.com/l-y-h/p/11385295.html
注:
头节点(非必须):仅用于作为链表起点,放在链表第一个节点前,无实际意义。
首节点:指链表第一个节点,即头节点后面的第一个节点。
头节点是非必须的,使用头节点是方便操作链表而设立的。如下代码实现采用 头节点 方式实现。
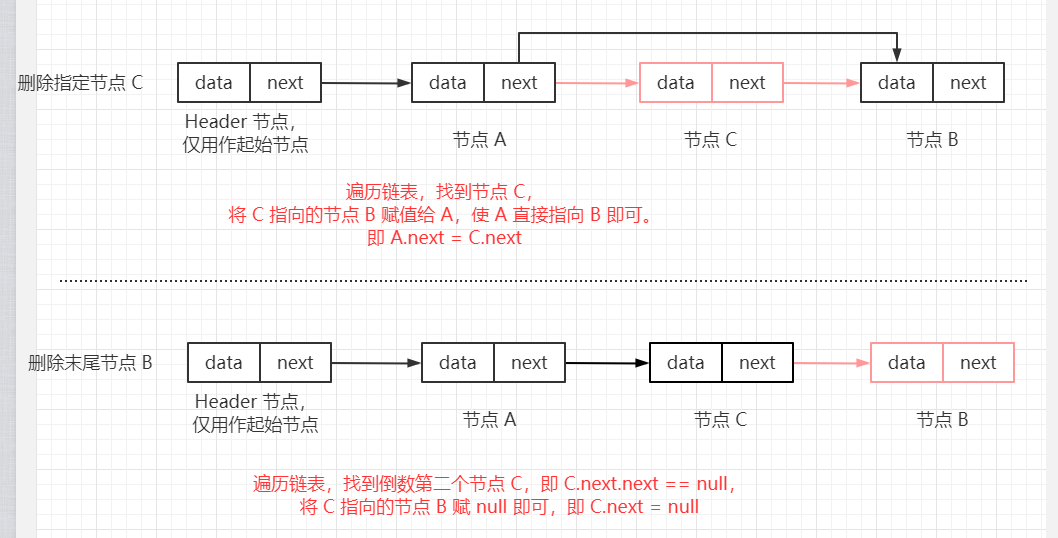
【模拟 指针形式 实现 单链表:】 模拟节点: 节点包括 数据域(保存数据) 以及 指针域(指向下一个节点)。 class Node<E> { E data; // 数据域,存储节点数据 Node next; // 指针域,指向下一个节点 public Node(E data) { this.data = data; } public Node(E data, Node<E> next) { this.data = data; this.next = next; } } 【增删节点:】 直接添加节点 A 到链表末尾: 先得遍历得到最后一个节点 B 所在位置,条件为: B.next == null, 然后将最后一个节点 B 的 next 指向该节点, 即 B.next = A。 向指定位置插入节点: 比如: A->B 中插入 C, 即 A->C->B,此时,先让 C 指向 B,再让 A 指向 C。 即 C.next = A.next; // 此时 A.next = B A.next = C; 直接删除链表末尾节点: 先遍历到倒数第二个节点 C 位置,条件为:C.next.next == null; 然后将其指向的下一个节点置为 null 即可,即 C.next = null。 删除指定位置的节点: 比如: A->C->B 中删除 C,此时,直接让 A 指向 B。 即: A.next = C.next;

【代码实现:】 package com.lyh.com.lyh.linkedlist; public class SingleLinkedList<E> { private int size; // 用于保存链表实际长度 private Node<E> header; // 用于保存链表头节点,仅用作 起点,不存储数据。 public SingleLinkedList(Node<E> header) { this.header = header; } /** * 在链表末尾添加节点 * @param data 节点数据 */ public void addLastNode(E data) { Node<E> newNode = new Node<>(data); // 根据数据创建一个 新节点 Node<E> temp = header; // 使用临时变量保存头节点,用于辅助遍历链表 // 遍历链表 while(temp.next != null) { temp = temp.next; } // 在链表末尾添加节点,链表长度加 1 temp.next = newNode; size++; } /** * 在链表末尾添加节点 * @param newNode 节点 */ public void addLastNode(Node<E> newNode) { Node<E> temp = header; // 使用临时变量保存头节点,用于辅助遍历链表 // 遍历链表 while(temp.next != null) { temp = temp.next; } // 在链表末尾添加节点,链表长度加 1 temp.next = newNode; size++; } /** * 在链表指定位置 插入节点 * @param node 待插入节点 * @param index 指定位置(1 ~ n, 1 表示第一个节点位置) */ public void insert(Node<E> node, int index) { Node<E> temp = header; // 使用临时变量保存头节点,用于辅助遍历链表 // 节点越界则抛出异常 if (index < 1 || index > size) { throw new IndexOutOfBoundsException("Index: " + index + ", Size: " + size); } // 若节点为链表末尾,则调用 末尾添加 节点的方法 if (index == size) { addLastNode(node); return; } // 若节点不是链表末尾,则遍历找到插入位置 while(index != 1) { temp = temp.next; index--; } // A -> B 变为 A -> C -> B, 即 A.next = B 变为 C.next = A.next, A.next = C,即 A 指向 C,C 指向 B。 node.next = temp.next; temp.next = node; size++; } /** * 返回链表长度 * @return 链表长度 */ public int size() { return size; } /** * 输出链表 */ public void showList() { Node<E> temp = header.next; // 使用临时变量保存第一个节点,用于辅助遍历链表 if (size == 0) { System.out.println("当前链表为空"); return; } // 链表不为空时遍历链表 System.out.print("当前链表长度为: " + size + " 当前链表为: "); while(temp != null) { System.out.print(temp + " ===> "); temp = temp.next; } System.out.println(); } /** * 删除最后一个节点 */ public void deleteLastNode() { Node<E> temp = header; // 使用临时变量保存头节点,用于遍历链表 if (size == 0) { System.out.println("当前链表为空,无需删除"); return; } while(temp.next.next != null) { temp = temp.next; } temp.next = null; size--; } /** * 删除指定位置的元素 * @param index 指定位置(1 ~ n, 1 表示第一个节点位置) */ public void delete(int index) { Node<E> temp = header; // 使用临时变量保存头节点,用于辅助遍历链表 // 节点越界则抛出异常 if (index < 1 || index > size) { throw new IndexOutOfBoundsException("Index: " + index + ", Size: " + size); } // 若节点为链表末尾,则调用 末尾删除 节点的方法 if (index == size) { deleteLastNode(); return; } // 遍历链表,找到删除位置 while(index != 1) { index--; temp = temp.next; } // A -> C -> B 变为 A -> B,即 A.next = C, C.next = B 变为 A.next = C.next,即 A 直接指向 B temp.next = temp.next.next; size--; } public static void main(String[] args) { // 创建一个单链表 SingleLinkedList<String> singleLinkedList = new SingleLinkedList(new Node("Header")); // 输出,此时链表为空 singleLinkedList.showList(); System.out.println("======================================="); // 给链表添加数据 singleLinkedList.addLastNode("Java"); singleLinkedList.addLastNode(new Node<>("JavaScript")); singleLinkedList.insert(new Node<>("Phthon"), 1); singleLinkedList.insert(new Node<>("C"), 3); // 输出链表 singleLinkedList.showList(); System.out.println("======================================="); // 删除链表数据 singleLinkedList.deleteLastNode(); singleLinkedList.delete(2); // 输出链表 singleLinkedList.showList(); System.out.println("======================================="); } } class Node<E> { E data; // 数据域,存储节点数据 Node<E> next; // 指针域,指向下一个节点 public Node(E data) { this.data = data; } public Node(E data, Node<E> next) { this.data = data; this.next = next; } @Override public String toString() { return "Node{ data = " + data + " }"; } } 【输出结果:】 当前链表为空 ======================================= 当前链表长度为: 4 当前链表为: Node{ data = Phthon } ===> Node{ data = Java } ===> Node{ data = JavaScript } ===> Node{ data = C } ===> ======================================= 当前链表长度为: 2 当前链表为: Node{ data = Phthon } ===> Node{ data = JavaScript } ===> =======================================
(3)常见的单链表笔试题
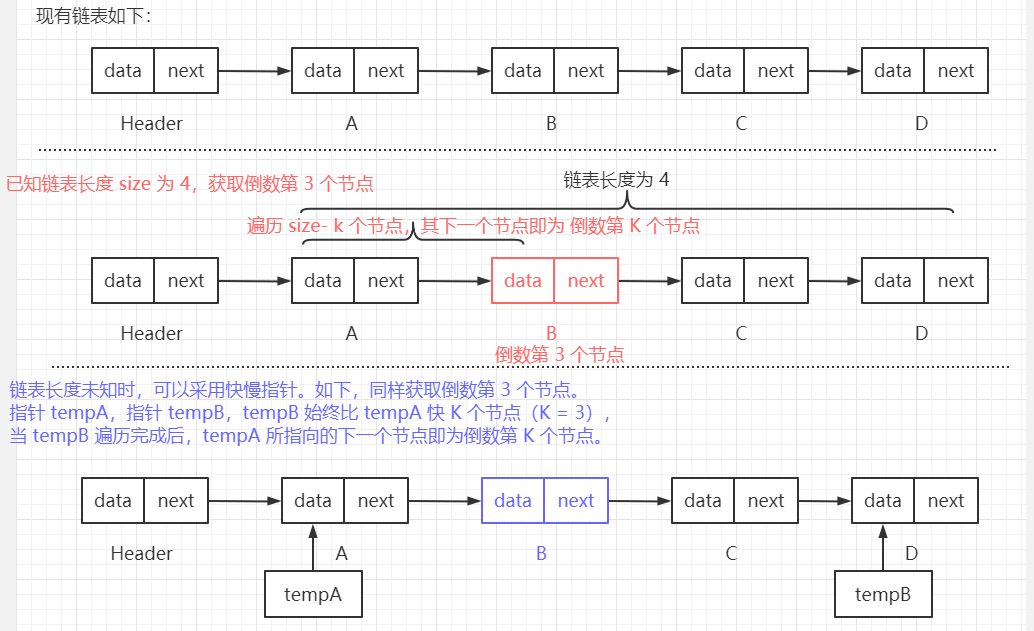
【笔试题一:】 找到当前链表中倒数 第 K 个节点。 【笔试题一解决思路:】 思路一: 链表长度 size 可知时,则可以遍历 size - k 个节点,从而找到倒数第 K 个节点。 当然 size 可以通过遍历一遍链表得到,这会消耗时间。 思路二: 链表长度 size 未知时,可使用 快慢指针 解决。 使用两个指针 A、B 同时遍历,且指针 B 始终比指针 A 快 K 个节点, 当 指针 B 遍历到链表末尾时,此时 指针 A 指向的下一个节点即为倒数第 K 个节点。 【核心代码如下:】 /** * 获取倒数第 K 个节点。 * 方式一: * size 可知,遍历 size - k 个节点即可 * @param k K 值,(1 ~ n,1 表示倒数第一个节点) * @return 倒数第 K 个节点 */ public Node<E> getLastKNode(int k) { Node<E> temp = header.next; // 使用临时变量存储第一个节点,用于辅助链表遍历 // 判断节点是否越界 if (k < 1 || k > size) { throw new IndexOutOfBoundsException("Index: " + k + ", Size: " + size); } // 遍历 size - k 个节点,即可找到倒数第 K 个节点 for (int i = 0; i < size - k; i++) { temp = temp.next; } return temp; } /** * 获取倒数第 K 个节点。 * 方式二: * size 未知时,使用快慢节点, * 节点 A 比节点 B 始终快 k 个节点,A,B 同时向后遍历,当 A 遍历完成后,B 遍历的位置下一个位置即为倒数第 K 个节点。 * @param k K 值,(1 ~ n,1 表示倒数第一个节点) * @return 倒数第 K 个节点 */ public Node<E> getLastKNode2(int k) { Node<E> tempA = header; // 使用临时变量存储头节点,用于辅助链表遍历 Node<E> tempB = header; // 使用临时变量存储头节点,用于辅助链表遍历 // 节点越界判断 if (k < 1) { throw new IndexOutOfBoundsException("Index: " + k); } // A 比 B 快 K 个节点 while(tempA.next != null && k != 0) { tempA = tempA.next; k--; } // 节点越界判断 if (k != 0) { throw new IndexOutOfBoundsException("K 值大于链表长度"); } // 遍历,当 A 到链表末尾时,B 所处位置下一个位置即为倒数第 K 个节点 while(tempA.next != null) { tempA = tempA.next; tempB = tempB.next; } return tempB.next; }
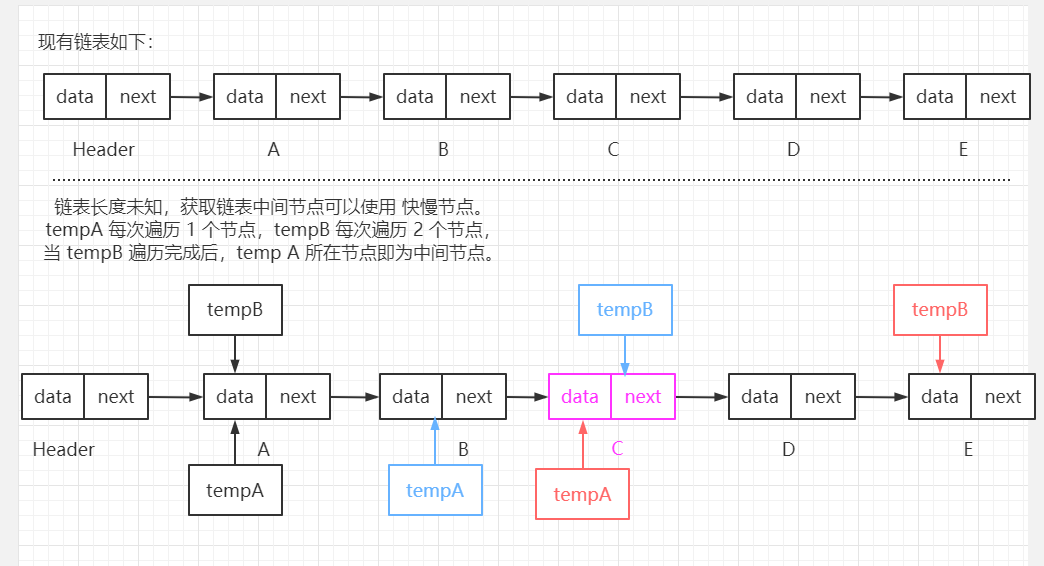
【笔试题二:】 找到当前链表的中间节点(链表长度未知)。 【笔试题二解决思路:】 链表长度未知,可以采用 快慢指针 方式解决。 此处与解决 上题 倒数第 K 个节点类似,只是此时节点 B 比 节点 A 每次都快 1 个节点(即 A 每次遍历移动一个节点,B 会遍历移动两个节点)。 【核心代码如下:】 /** * 链表长度未知时,获取链表中间节点 * @return 链表中间节点 */ public Node<E> getHalfNode() { Node<E> tempA = header.next; // 使用临时变量保存第一个节点,用于辅助遍历链表 Node<E> tempB = header.next; // 使用临时变量保存第一个节点,用于辅助遍历链表 // 循环遍历 B 节点,B 节点每次都比 A 节点快一个节点(每次多走一个节点),所以当 B 遍历完成后,A 节点所处位置即为中间节点。 while(tempB.next != null && tempB.next.next != null) { tempA = tempA.next; tempB = tempB.next.next; } return tempA; }
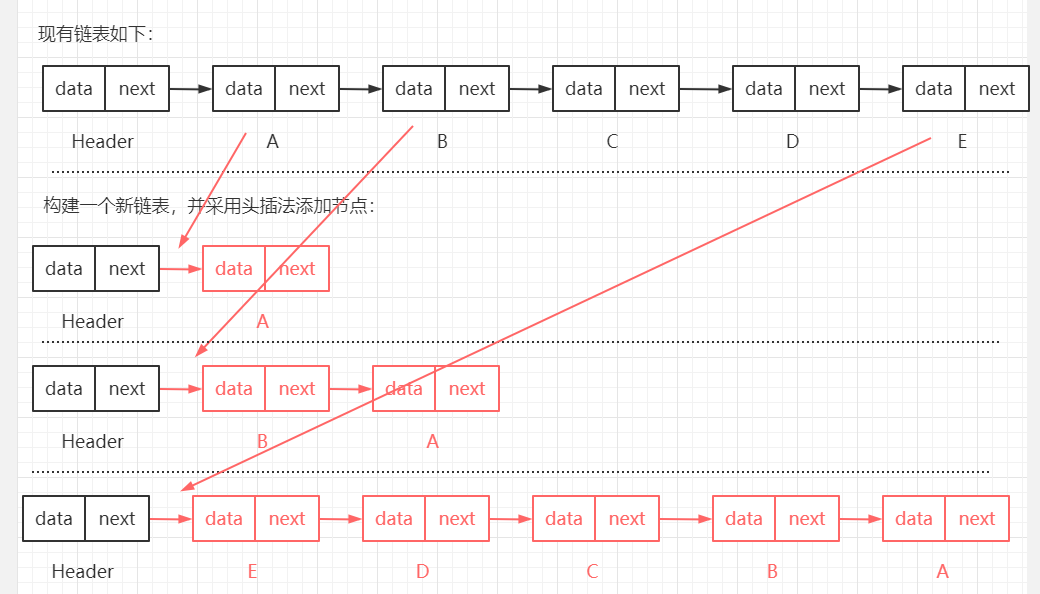
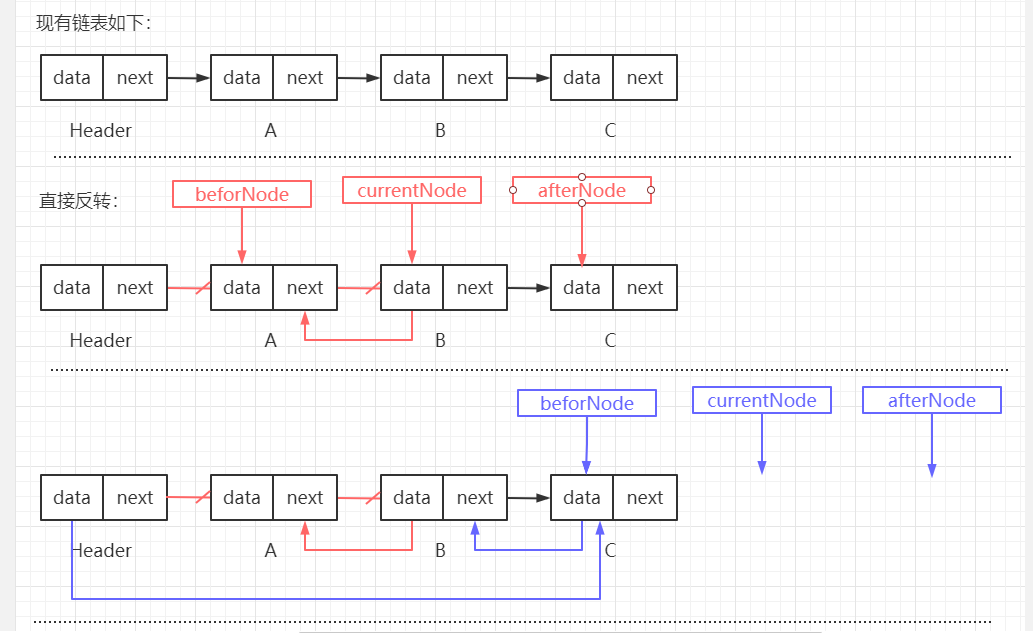
【笔试题三:】 反转链表。 【笔试题三解决思路:】 思路一: 头插法,新建一个链表,遍历原始链表,将每个节点通过头插法插入新链表。 头插法,即每次均在第一个节点位置处进行插入操作。 思路二: 直接反转。 通过三个指针来辅助,beforeNode、currentNode、afterNode,此时 beforeNode -> currentNode -> afterNode。 其中: beforeNode 为当前节点上一个节点。 currentNode 为当前节点。 afterNode 为当前节点下一个节点。 遍历链表,使 currentNode -> beforeNode。 【核心代码如下:】 /** * 链表反转。 * 方式一: * 头插法,新建一个链表,遍历原始链表,将每个节点通过头插法插入新链表。 * @return */ public SingleLinkedList<E> reverseList() { Node<E> temp = header.next; // 使用临时变量存储第一个节点,用于辅助遍历原链表 SingleLinkedList singleLinkedList = new SingleLinkedList(new Node("newHeader")); // 新建一个链表 // 若原链表为空,则直接返回 空的 新链表 if (temp == null) { return singleLinkedList; } // 遍历原链表,并调用新链表的 头插法添加节点 while(temp != null) { singleLinkedList.addFirstNode(new Node(temp.data)); temp = temp.next; } return singleLinkedList; } /** * 头插法插入节点,每次均在第一个节点位置处进行插入 * @param node 待插入节点 */ public void addFirstNode(Node<E> node) { Node<E> temp = header.next; // 使用临时变量保存第一个节点,用于辅助遍历链表 // 若链表为空,则直接赋值即可 if (temp == null) { header.next = node; size++; return; } // 若链表不为空,则在第一个节点位置进行插入 node.next = temp; header.next = node; size++; } /** * 链表反转。 * 方式二: * 直接反转,通过三个指针进行辅助。此方式会直接变化当前链表。 */ public void reverseList2() { // 链表为空直接返回 if (header.next == null) { System.out.println("当前链表为空"); return; } Node<E> beforeNode = null; // 指向当前节点的上个节点 Node<E> currentNode = header.next; // 指向当前节点 Node<E> afterNode = null; // 指向当前节点的下一个节点 // 遍历节点 while(currentNode != null) { afterNode = currentNode.next; // 获取当前节点的下一个节点 currentNode.next = beforeNode; // 将当前节点指向上一个节点 beforeNode = currentNode; // 上一个节点后移 currentNode = afterNode; // 当前节点后移,为了下一个遍历 } header.next = beforeNode; // 遍历结束后,beforeNode 为最后一个节点,使用 头节点 指向该节点,即可完成链表反转 }
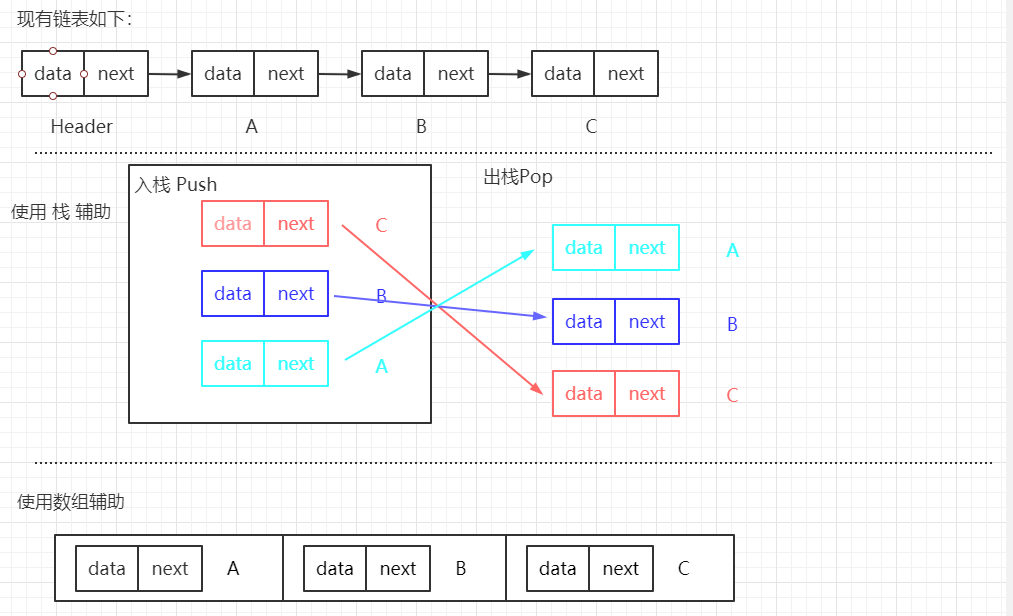
【笔试题四:】 打印输出反转链表,不能反转原链表。 【笔试题四解决思路:】 思路一(此处不重复演示,详见上例代码): 由于不能反转原链表,可以与上例头插法相同, 新建一个链表并使用头插法添加节点,最后遍历输出新链表。 思路二: 使用栈进行辅助。栈属于先进后出结构。 可以先遍历链表并存入栈中,然后依次取出栈顶元素即可。 思路三: 使用数组进行辅助(有序结构存储一般均可,比如 TreeMap 存储,根据 key 倒序输出亦可)。 遍历链表并存入数组,然后反序输出数组即可(注:若是反序存入数组,可以顺序输出)。 【核心代码如下:】 /** * 不改变当前链表下,反序输出链表。 * 方式一: * 借用栈结构进行辅助。栈是先进后出结构。 * 先遍历链表并依次存入栈,然后从栈顶挨个取出数据,即可得到反序链表。 */ public void printReverseList() { Node<E> temp = header.next; // 使用临时变量保存第一个节点,用于辅助链表遍历 Stack<Node<E>> stack = new Stack(); // 使用栈存储节点 // 判断链表是否为空 if (temp == null) { System.out.println("当前链表为空"); return; } // 遍历节点,使用栈存储链表各节点。 while(temp != null) { stack.push(temp); temp = temp.next; } // 遍历输出栈 while(stack.size() > 0) { System.out.print(stack.pop() + "==>"); } System.out.println(); } /** * 不改变当前链表下,反序输出链表。 * 方式二: * 采用数组辅助。 * 遍历链表存入数组,最后反序输出数组即可(注:若是反序存入数组,可以顺序输出)。 */ public void printReverseList2() { Node<E> temp = header.next; // 使用临时变量保存第一个节点,用于辅助链表遍历 int length = size(); Node<E>[] nodes = new Node[length]; // 使用数组存储链表节点 // 判断链表是否为空 if(temp == null) { System.out.println("当前链表为空"); return; } // 遍历链表,存入数组,此处反序存入数组,后面顺序输出即可 while(temp != null) { nodes[--length] = temp; temp = temp.next; } System.out.println(Arrays.toString(nodes)); }
上述所有单链表相关代码完整版如下(有部分地方还需修改,仅供参考):

【代码:】 package com.lyh.com.lyh.linkedlist; import java.util.Arrays; import java.util.Stack; public class SingleLinkedList<E> { private int size; // 用于保存链表实际长度 private Node<E> header; // 用于保存链表头节点,仅用作 起点,不存储数据。 public SingleLinkedList(Node<E> header) { this.header = header; } /** * 在链表末尾添加节点 * @param data 节点数据 */ public void addLastNode(E data) { Node<E> newNode = new Node<>(data); // 根据数据创建一个 新节点 Node<E> temp = header; // 使用临时变量保存头节点,用于辅助遍历链表 // 遍历链表 while(temp.next != null) { temp = temp.next; } // 在链表末尾添加节点,链表长度加 1 temp.next = newNode; size++; } /** * 在链表末尾添加节点 * @param newNode 节点 */ public void addLastNode(Node<E> newNode) { Node<E> temp = header; // 使用临时变量保存头节点,用于辅助遍历链表 // 遍历链表 while(temp.next != null) { temp = temp.next; } // 在链表末尾添加节点,链表长度加 1 temp.next = newNode; size++; } /** * 在链表指定位置 插入节点 * @param node 待插入节点 * @param index 指定位置(1 ~ n, 1 表示第一个节点位置) */ public void insert(Node<E> node, int index) { Node<E> temp = header; // 使用临时变量保存头节点,用于辅助遍历链表 // 节点越界则抛出异常 if (index < 1 || index > size) { throw new IndexOutOfBoundsException("Index: " + index + ", Size: " + size); } // 若节点为链表末尾,则调用 末尾添加 节点的方法 if (index == size) { addLastNode(node); return; } // 若节点不是链表末尾,则遍历找到插入位置 while (index != 1) { temp = temp.next; index--; } // A -> B 变为 A -> C -> B, 即 A.next = B 变为 C.next = A.next, A.next = C,即 A 指向 C,C 指向 B。 node.next = temp.next; temp.next = node; size++; } /** * 返回链表长度 * @return 链表长度 */ public int size() { return size; } /** * 输出链表 */ public void showList() { Node<E> temp = header.next; // 使用临时变量保存第一个节点,用于辅助遍历链表 if (size == 0) { System.out.println("当前链表为空"); return; } // 链表不为空时遍历链表 System.out.print("当前链表长度为: " + size + " 当前链表为: "); while(temp != null) { System.out.print(temp + " ===> "); temp = temp.next; } System.out.println(); } /** * 删除最后一个节点 */ public void deleteLastNode() { Node<E> temp = header; // 使用临时变量保存头节点,用于遍历链表 if (size == 0) { System.out.println("当前链表为空,无需删除"); return; } while(temp.next.next != null) { temp = temp.next; } temp.next = null; size--; } /** * 删除指定位置的元素 * @param index 指定位置(1 ~ n, 1 表示第一个节点位置) */ public void delete(int index) { Node<E> temp = header; // 使用临时变量保存头节点,用于辅助遍历链表 // 节点越界则抛出异常 if (index < 1 || index > size) { throw new IndexOutOfBoundsException("Index: " + index + ", Size: " + size); } // 若节点为链表末尾,则调用 末尾删除 节点的方法 if (index == size) { deleteLastNode(); return; } // 遍历链表,找到删除位置 while(index != 1) { index--; temp = temp.next; } // A -> C -> B 变为 A -> B,即 A.next = C, C.next = B 变为 A.next = C.next,即 A 直接指向 B temp.next = temp.next.next; size--; } /** * 获取倒数第 K 个节点。 * 方式一: * size 可知,遍历 size - k 个节点即可 * @param k K 值,(1 ~ n,1 表示倒数第一个节点) * @return 倒数第 K 个节点 */ public Node<E> getLastKNode(int k) { Node<E> temp = header.next; // 使用临时变量存储第一个节点,用于辅助链表遍历 // 判断节点是否越界 if (k < 1 || k > size) { throw new IndexOutOfBoundsException("Index: " + k + ", Size: " + size); } // 遍历 size - k 个节点,即可找到倒数第 K 个节点 for (int i = 0; i < size - k; i++) { temp = temp.next; } return temp; } /** * 获取倒数第 K 个节点。 * 方式二: * size 未知时,使用快慢节点, * 节点 A 比节点 B 始终快 k 个节点,A,B 同时向后遍历,当 A 遍历完成后,B 遍历的位置下一个位置即为倒数第 K 个节点。 * @param k K 值,(1 ~ n,1 表示倒数第一个节点) * @return 倒数第 K 个节点 */ public Node<E> getLastKNode2(int k) { Node<E> tempA = header; // 使用临时变量存储头节点,用于辅助链表遍历 Node<E> tempB = header; // 使用临时变量存储头节点,用于辅助链表遍历 // 节点越界判断 if (k < 1) { throw new IndexOutOfBoundsException("Index: " + k); } // A 比 B 快 K 个节点 while(tempA.next != null && k != 0) { tempA = tempA.next; k--; } // 节点越界判断 if (k != 0) { throw new IndexOutOfBoundsException("K 值大于链表长度"); } // 遍历,当 A 到链表末尾时,B 所处位置下一个位置即为倒数第 K 个节点 while(tempA.next != null) { tempA = tempA.next; tempB = tempB.next; } return tempB.next; } /** * 链表长度未知时,获取链表中间节点 * @return 链表中间节点 */ public Node<E> getHalfNode() { Node<E> tempA = header.next; // 使用临时变量保存第一个节点,用于辅助遍历链表 Node<E> tempB = header.next; // 使用临时变量保存第一个节点,用于辅助遍历链表 // 循环遍历 B 节点,B 节点每次都比 A 节点快一个节点(每次多走一个节点),所以当 B 遍历完成后,A 节点所处位置即为中间节点。 while(tempB.next != null && tempB.next.next != null) { tempA = tempA.next; tempB = tempB.next.next; } return tempA; } /** * 链表反转。 * 方式一: * 头插法,新建一个链表,遍历原始链表,将每个节点通过头插法插入新链表。 * @return */ public SingleLinkedList<E> reverseList() { Node<E> temp = header.next; // 使用临时变量存储第一个节点,用于辅助遍历原链表 SingleLinkedList singleLinkedList = new SingleLinkedList(new Node("newHeader")); // 新建一个链表 // 若原链表为空,则直接返回 空的 新链表 if (temp == null) { return singleLinkedList; } // 遍历原链表,并调用新链表的 头插法添加节点 while(temp != null) { singleLinkedList.addFirstNode(new Node(temp.data)); temp = temp.next; } return singleLinkedList; } /** * 头插法插入节点,每次均在第一个节点位置处进行插入 * @param node 待插入节点 */ public void addFirstNode(Node<E> node) { Node<E> temp = header.next; // 使用临时变量保存第一个节点,用于辅助遍历链表 // 若链表为空,则直接赋值即可 if (temp == null) { header.next = node; size++; return; } // 若链表不为空,则在第一个节点位置进行插入 node.next = temp; header.next = node; size++; } /** * 链表反转。 * 方式二: * 直接反转,通过三个指针进行辅助。此方式会直接变化当前链表。 */ public void reverseList2() { // 链表为空直接返回 if (header.next == null) { System.out.println("当前链表为空"); return; } Node<E> beforeNode = null; // 指向当前节点的上个节点 Node<E> currentNode = header.next; // 指向当前节点 Node<E> afterNode = null; // 指向当前节点的下一个节点 // 遍历节点 while(currentNode != null) { afterNode = currentNode.next; // 获取当前节点的下一个节点 currentNode.next = beforeNode; // 将当前节点指向上一个节点 beforeNode = currentNode; // 上一个节点后移 currentNode = afterNode; // 当前节点后移,为了下一个遍历 } header.next = beforeNode; // 遍历结束后,beforeNode 为最后一个节点,使用 头节点 指向该节点,即可完成链表反转 } /** * 不改变当前链表下,反序输出链表。 * 方式一: * 借用栈结构进行辅助。栈是先进后出结构。 * 先遍历链表并依次存入栈,然后从栈顶挨个取出数据,即可得到反序链表。 */ public void printReverseList() { Node<E> temp = header.next; // 使用临时变量保存第一个节点,用于辅助链表遍历 Stack<Node<E>> stack = new Stack(); // 使用栈存储节点 // 判断链表是否为空 if (temp == null) { System.out.println("当前链表为空"); return; } // 遍历节点,使用栈存储链表各节点。 while(temp != null) { stack.push(temp); temp = temp.next; } // 遍历输出栈 while(stack.size() > 0) { System.out.print(stack.pop() + "==>"); } System.out.println(); } /** * 不改变当前链表下,反序输出链表。 * 方式二: * 采用数组辅助。 * 遍历链表存入数组,最后反序输出数组即可(注:若是反序存入数组,可以顺序输出)。 */ public void printReverseList2() { Node<E> temp = header.next; // 使用临时变量保存第一个节点,用于辅助链表遍历 int length = size(); Node<E>[] nodes = new Node[length]; // 使用数组存储链表节点 // 判断链表是否为空 if(temp == null) { System.out.println("当前链表为空"); return; } // 遍历链表,存入数组,此处反序存入数组,后面顺序输出即可 while(temp != null) { nodes[--length] = temp; temp = temp.next; } System.out.println(Arrays.toString(nodes)); } public static void main(String[] args) { // 创建一个单链表 SingleLinkedList<String> singleLinkedList = new SingleLinkedList(new Node("Header")); // 输出,此时链表为空 singleLinkedList.showList(); System.out.println("======================================="); // 给链表添加数据 singleLinkedList.addLastNode("Java"); singleLinkedList.addLastNode(new Node<>("JavaScript")); singleLinkedList.insert(new Node<>("Phthon"), 1); singleLinkedList.insert(new Node<>("C"), 3); // 输出链表 singleLinkedList.showList(); System.out.println("======================================="); // 删除链表数据 // singleLinkedList.deleteLastNode(); // singleLinkedList.delete(2); // // 输出链表 // singleLinkedList.showList(); // System.out.println("======================================="); // 获取倒数第 k 个节点 // System.out.println(singleLinkedList.getLastKNode(1)); // System.out.println(singleLinkedList.getLastKNode2(2)); System.out.println("======================================="); // 获取链表中间节点 // System.out.println(singleLinkedList.getHalfNode()); System.out.println("======================================="); // 反转链表(头插法新建一个新的链表) SingleLinkedList singleLinkedList2 = singleLinkedList.reverseList(); singleLinkedList2.showList(); System.out.println("======================================="); // 反转链表(直接反转) singleLinkedList2.reverseList2(); singleLinkedList2.showList(); System.out.println("======================================="); // 不改变原链表下,反序输出链表(借助栈实现) singleLinkedList2.printReverseList(); System.out.println("======================================="); // 不改变原链表下,反序输出链表(借助数组实现) singleLinkedList2.printReverseList2(); System.out.println("======================================="); } } class Node<E> { E data; // 数据域,存储节点数据 Node<E> next; // 指针域,指向下一个节点 public Node(E data) { this.data = data; } public Node(E data, Node<E> next) { this.data = data; this.next = next; } @Override public String toString() { return "Node{ data = " + data + " }"; } } 【输出结果:】 当前链表为空 ======================================= 当前链表长度为: 4 当前链表为: Node{ data = Phthon } ===> Node{ data = Java } ===> Node{ data = JavaScript } ===> Node{ data = C } ===> ======================================= 当前链表长度为: 2 当前链表为: Node{ data = Phthon } ===> Node{ data = JavaScript } ===> ======================================= Node{ data = JavaScript } Node{ data = Phthon } ======================================= Node{ data = Phthon } ======================================= 当前链表长度为: 2 当前链表为: Node{ data = JavaScript } ===> Node{ data = Phthon } ===> ======================================= 当前链表长度为: 2 当前链表为: Node{ data = Phthon } ===> Node{ data = JavaScript } ===> ======================================= Node{ data = JavaScript }==>Node{ data = Phthon }==> ======================================= [Node{ data = JavaScript }, Node{ data = Phthon }] =======================================
4、链表(Linked list)-- 双向链表、环形链表(约瑟夫环)
(1)双向链表
通过上面单链表相关操作,可以知道 单链表的 查找方向唯一。
而双向链表在 单链表的 基础上在 添加一个指针域(pre),这个指针域用来指向 当前节点的上一个节点,从而实现 链表 双向查找(某种程度上提高查找效率)。
【使用指针 模拟实现 双向链表:】 模拟节点: 在单链表的基础上,增加了一个 指向上一个节点的 指针域。 class Node2<E> { Node<E> pre; // 指针域,指向当前节点的上一个节点 Node<E> next; // 指针域,指向当前节点的下一个节点 E data; // 数据域,存储节点数据 public Node2(E data) { this.data = data; } public Node2(E data, Node<E> pre, Node<E> next) { this.data = data; this.pre = pre; this.next = next; } } 【增删节点:】 直接添加节点 A 到链表末尾: 首先得遍历到链表最后一个节点 B 的位置,条件: B.next = null。 然后将 B 下一个节点指向 A, A 上一个节点指向 B。即 B.next = A; A.pre = B。 指定位置添加节点 C: 比如: A -> B 变为 A -> C -> B。 即 A.next = B; B.pre = A; 变为 C.next = B; C.pre = B.pre; B.pre.next = C; B.pre = C; 直接删除链表末尾节点 A: 遍历到链表最后一个节点 B 的位置,然后将其下一个节点指向 null 即可,即 B.next = null; 删除指定位置的节点 C: 比如: A -> C -> B 变为 A -> B。 C.pre.next = C.next; C.next.pre = C.pre;


(2)双向链表代码实现如下:
【代码实现:】 package com.lyh.com.lyh.linkedlist; public class DoubleLinkedList<E> { private int size = 0; // 用于保存链表实际长度 private Node2<E> header; // 用于保存链表头节点,仅用作 起点,不存储数据。 public DoubleLinkedList(Node2<E> header) { this.header = header; } /** * 直接在链表末尾添加节点 * @param node 待添加节点 */ public void addLastNode(Node2<E> node) { Node2<E> temp = header; // 使用临时变量保存头节点,用于辅助链表遍历 // 遍历链表至链表末尾 while(temp.next != null) { temp = temp.next; } // 添加节点 temp.next = node; node.pre = temp; size++; } /** * 直接在链表末尾添加节点 * @param data 待添加数据 */ public void addLastNode2(E data) { Node2<E> temp = header; // 使用临时节点保存头节点,用于辅助链表遍历 Node2<E> newNode = new Node2<>(data); // 创建新节点 // 遍历链表至链表末尾 while(temp.next != null) { temp = temp.next; } // 添加节点 temp.next = newNode; newNode.pre = temp; size++; } /** * 遍历输出链表 */ public void showList() { Node2<E> temp = header.next; // 使用临时变量保存第一个节点,用于辅助遍历链表 // 判断链表是否为空 if(temp == null) { System.out.println("当前链表为空"); return; } // 遍历输出链表 System.out.print("当前链表长度为: " + size() + " == 当前链表为: "); while(temp != null) { System.out.print(temp + " ==> "); temp = temp.next; } System.out.println(); } /** * 返回链表长度 * @return 链表长度 */ public int size() { return this.size; } /** * 在指定位置添加节点 * @param index 1 ~ n(1 表示 第一个节点) */ public void insert(int index, Node2<E> newNode) { Node2<E> temp = header; // 使用临时变量保存头节点,用于辅助链表遍历 // 遍历找到指定位置 while(index != 0 && temp.next != null) { temp = temp.next; index--; } if (index != 0) { throw new IndexOutOfBoundsException("指定位置有误: " + index); } newNode.next = temp; newNode.pre = temp.pre; temp.pre.next = newNode; temp.pre = newNode; size++; } /** * 删除指定位置的节点 * @param index 1 ~ n(1 表示第一个节点) */ public void delete(int index) { Node2<E> temp = header; // 使用临时变量保存头节点,用于辅助链表遍历 // 遍历找到待删除节点位置 while(index != 0 && temp.next != null) { index--; temp = temp.next; } // 判断节点是否存在 if (index != 0) { throw new IndexOutOfBoundsException("指定节点位置不存在"); } temp.pre.next = temp.next; // 若节点为最后一个节点,则无需对下一个节点进行赋值操作 if (temp.next != null) { temp.next.pre = temp.pre; } size--; } /** * 直接删除链表末尾节点 */ public void deleteLastNode() { Node2<E> temp = header; // 使用临时变量保存头节点,用于辅助链表遍历 // 判断链表是否为空 if (temp.next == null) { System.out.println("当前链表为空"); return; } // 遍历链表至最后一个节点 while(temp.next != null) { temp = temp.next; } temp.pre.next = null; size--; } public static void main(String[] args) { // 创建双向链表 DoubleLinkedList<String> doubleLinkedList = new DoubleLinkedList<>(new Node2<>("header")); // 输出链表 doubleLinkedList.showList(); System.out.println("=========================="); // 添加节点 doubleLinkedList.addLastNode(new Node2<>("Java")); doubleLinkedList.addLastNode2("JavaScript"); doubleLinkedList.insert(2, new Node2<>("E")); doubleLinkedList.insert(1, new Node2<>("F")); // 输出链表 doubleLinkedList.showList(); System.out.println("=========================="); doubleLinkedList.delete(1); doubleLinkedList.deleteLastNode(); // 输出链表 doubleLinkedList.showList(); System.out.println("=========================="); } } class Node2<E> { Node2<E> pre; // 指针域,指向当前节点的上一个节点 Node2<E> next; // 指针域,指向当前节点的下一个节点 E data; // 数据域,存储节点数据 public Node2(E data) { this.data = data; } public Node2(E data, Node2<E> pre, Node2<E> next) { this.data = data; this.pre = pre; this.next = next; } @Override public String toString() { return "Node2{ pre= " + (pre != null ? pre.data : null) + ", next= " + (next != null ? next.data : null) + ", data= " + data + '}'; } } 【输出结果:】 当前链表为空 ========================== 当前链表长度为: 4 == 当前链表为: Node2{ pre= header, next= Java, data= F} ==> Node2{ pre= F, next= E, data= Java} ==> Node2{ pre= Java, next= JavaScript, data= E} ==> Node2{ pre= E, next= null, data= JavaScript} ==> ========================== 当前链表长度为: 2 == 当前链表为: Node2{ pre= header, next= E, data= Java} ==> Node2{ pre= Java, next= null, data= E} ==> ==========================
(3)单向环形链表
单向循环链表 指的是 在单链表基础上,将 最后一个节点的指针域 指向第一个节点,从而使链表变成一个环状结构。
其最常见的应用场景就是 约瑟夫环 问题。
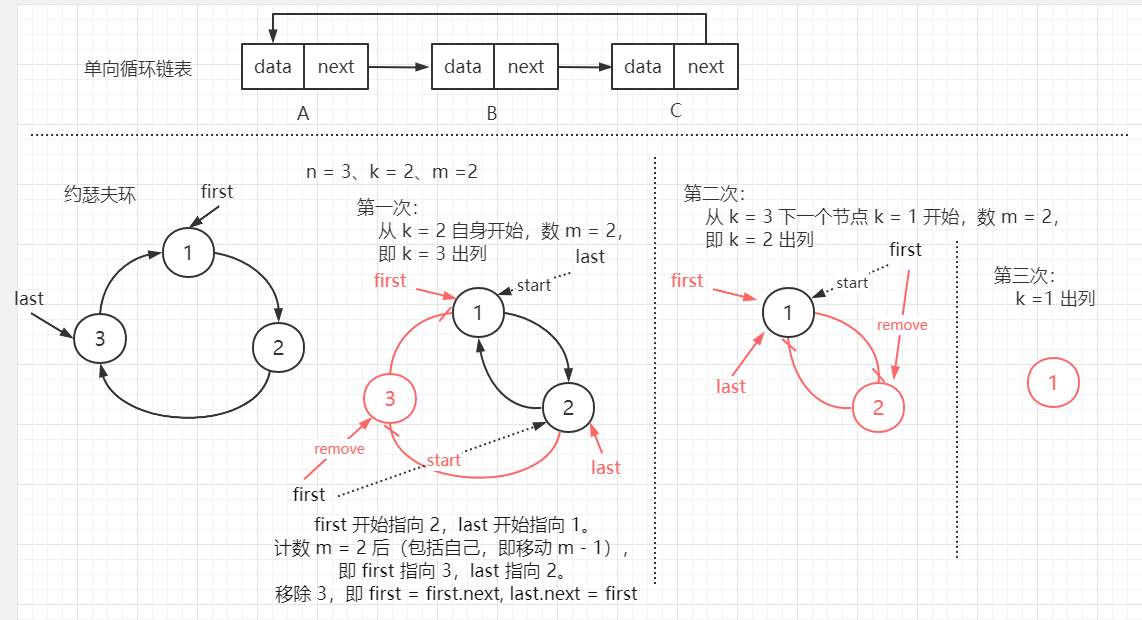
【约瑟夫(josephu)环问题:】 已知 n 个人围成一圈,编号由 1 ~ n,从编号为 k (1 <= k <= n)的人开始从 1 报数,数到 m 的那个人出列。 并从下一个人开始重新报数,再次数到 m 的人出列,依次类推,直至所有人出列,问 n 个人的出队编号(或者最后一个出队的是谁)。 【解决思路:】 使用一个不带头节点的单向循环链表处理。 先构成一个有 n 个节点的单向循环链表(构建一个单链表,并另最后一个节点 last 指向 第一个节点,即 last.next = first), 由 k 节点开始从 1 计数,移动 m 个节点后将对应的节点从链表中删除。并从下一个节点开始计数,直至最后一个节点。 使用 两个节点指针来辅助链表遍历 -- first(指向当前第一个节点、且用于表示待移除的节点)、last(指向当前最后一个节点)。 先遍历到 k 点(即 first 指向 k 点,last 指向 k 点上一个节点),计数(包括自身,所以 first、last 移动 m - 1 个节点), 此时 first 指向的即为待输出的节点,输出后,将其移除。即 first = first.next; last.next = first; 同理,从移除节点的下一个节点开始操作,当链表只剩最后一个节点,即 first == last 时,遍历结束,输出最后一个节点 即可。 注: last.next == first 表示环满 last == first 表示环空,即环里只有一个节点 【代码实现:】 package com.lyh.com.lyh.linkedlist; public class CircleSingleLinkedList<E> { private Node3<E> first; // 保存第一个节点 /** * 构成单向环形链表 * @param num 链表节点个数 (1 ~ n, 1 表示 1 个节点) */ public void addNode(int num) { // 判断 num 是否合适 if (num < 1) { throw new IndexOutOfBoundsException("数据不能构成环"); } Node3 temp = null; // 辅助指针,用于记录尾节点 // 添加节点,构成循环链表 for (int i = 1; i <= num; i++) { Node3 node = new Node3(i); // 构建新节点 if (i == 1) { // 只有一个节点时,即为首节点 first = node; temp = first; } else { // 添加尾节点 temp.next = node; temp = node; } } // 尾节点指向首节点,构成环 temp.next = first; } /** * 遍历输出当前环形链表 */ public void showList() { Node3<E> temp = first; // 使用临时变量存储第一个节点,用于辅助链表遍历 if (temp == null) { System.out.println("当前链表为空"); return; } System.out.print("当前链表为: "); while(temp.next != first) { System.out.print(temp + " ==> "); temp = temp.next; } System.out.println(temp); } /** * 按要求输出 移除节点 顺序 * @param num 节点总数(n) * @param start 开始节点编号(1 ~ n) * @param count 计数(1 ~ m) */ public void printList(int num, int start, int count) { Node3<E> last = first; // 用于记录当前链表最后一个节点 if (last == null || start < 1 || start > num) { throw new RuntimeException("参数不合法"); } // 遍历,得到最后一个节点 while(last.next != first) { last = last.next; } // 找到开始节点, first 表示开始节点,last 表示最后一个节点(即开始节点的上一个节点) while(start != 1) { last = last.next; first = first.next; start--; } // 遍历输出节点(开始节点、最后节点重合时 即链表只存在一个节点) while(last != first) { // 找到待移除节点,由于当前节点会被计算,所以只需移动 count - 1 个节点。 for (int i = 1; i < count; i++) { first = first.next; last = last.next; } System.out.print(first + " ==> "); // 移除节点(first 为被移除节点, 即 last -> first -> A 变为 fisrt = A 且 last -> A) first = first.next; last.next = first; } System.out.println(last); } public static void main(String[] args) { // 构建一个空的循环链表 CircleSingleLinkedList<Integer> circleSingleLinkedList = new CircleSingleLinkedList<>(); circleSingleLinkedList.showList(); System.out.println("========================"); // 添加节点 int num = 5; // 节点个数 circleSingleLinkedList.addNode(num); circleSingleLinkedList.showList(); System.out.println("========================"); // 输出节点 出链表顺序 int start = 2; // 开始编号 K int count = 2; // 计数 circleSingleLinkedList.printList(num, start, count); } } class Node3<E> { Node3<E> next; // 指针域,存储下一个节点 E data; // 数据域,存储节点数据 public Node3(E data) { this.data = data; } public Node3(Node3<E> next, E data) { this.next = next; this.data = data; } @Override public String toString() { return "Node3{ data= " + data + '}'; } } 【输出结果:】 当前链表为空 ======================== 当前链表为: Node3{ data= 1} ==> Node3{ data= 2} ==> Node3{ data= 3} ==> Node3{ data= 4} ==> Node3{ data= 5} ======================== Node3{ data= 3} ==> Node3{ data= 5} ==> Node3{ data= 2} ==> Node3{ data= 1} ==> Node3{ data= 4}
5、栈(Stack)
(1)什么是栈?
栈指的是一种 受限、线性的数据结构,其仅允许在 一端 进行插入(栈顶插入 push)、删除操作(栈顶删除 pop)。其允许插入、删除的一端为 栈顶(Top),另一端为栈底(Bottom)。
栈可以使用 数组 或者 链表 实现(一般采用数组实现,仅在首或尾增删,效率比链表高)。其遵循 先进后出(First In Last Out,FILO) 原则,即先存入 栈的值 后取出。

(2)常用场景:
二叉树遍历(迭代法)。
图的深度优先搜索法。
表达式转换与求值(比如:中缀表达式 转 后缀表达式)。
堆栈,比如:JVM 虚拟机栈 处理递归、子程序调用时,存储下一个指令地址 或者 参数、变量。
(3)使用数组模拟栈操作
【使用数组模拟栈操作:】 定义 top 用于记录当前栈顶指向,初始值为 -1。 数据 data 进栈时,top 先加 1 再赋值,即 stack[++top] = data。 数据 data 出栈时,先保存出栈的值,top 再减 1,即 data = stack[top--] 【代码实现:】 package com.lyh.stack; public class ArrayStack { private int maxSize; // 记录栈的大小(最大容量) private String[] stack; // 用于记录 private int top = -1; // 用于初始化栈顶位置 public ArrayStack(int maxSize) { this.maxSize = maxSize; this.stack = new String[maxSize]; } /** * 判断栈是否为空 * @return true 为空 */ public boolean isEmpty() { return top == -1; } /** * 判断栈是否已满 * @return true 表示已满 */ public boolean isFull() { return top == maxSize - 1; } /** * 数据入栈 * @param data 待入栈数据 */ public void push(String data) { // 判断栈是够已满,已满则不能再添加数据 if (isFull()) { System.out.println("栈满,无法添加"); return; } // top 加 1,并存值 this.stack[++top] = data; } /** * 数据出栈 * @return 出栈数据 */ public String pop() { // 判断栈是否为空,为空则无法返回数据 if(isEmpty()) { System.out.println("栈空,无数据"); return null; } // 取值,top 减 1 return this.stack[top--]; } /** * 遍历输出栈元素 */ public void showList() { // 判断栈是否为空 if (isEmpty()) { System.out.println("栈空"); return; } System.out.print("当前栈存储数据个数为: " + (top + 1) + " 当前栈输出为: "); for(int i = top; i >= 0; i--) { System.out.print(this.stack[i] + " == "); } System.out.println(); } public static void main(String[] args) { // 实例化栈 ArrayStack arrayStack = new ArrayStack(10); // 遍历栈 arrayStack.showList(); System.out.println("========================"); // 数据入栈 arrayStack.push("Java"); arrayStack.push("Python"); arrayStack.push("JavaScript"); // 遍历栈 arrayStack.showList(); System.out.println("========================"); // 数据出栈 System.out.println(arrayStack.pop()); System.out.println("========================"); // 遍历栈 arrayStack.showList(); System.out.println("========================"); } } 【输出结果:】 栈空 ======================== 当前栈存储数据个数为: 3 当前栈输出为: JavaScript == Python == Java == ======================== JavaScript ======================== 当前栈存储数据个数为: 2 当前栈输出为: Python == Java == ========================
6、使用栈计算 前缀(波兰)、中缀、逆波兰(后缀)表达式
(1)表达式的三种表示形式:
表达式可以分为三种表示形式:
前缀(波兰)表达式。其运算符在操作数之前。
中缀表达式。常见的算术公式(运算符在操作数中间),其括号不可省。
后缀(逆波兰)表达式。其运算符在操作数之后。
举例(以下为表达式的三种表示形式):
前缀表达式:+ 3 4
中缀表达式:3 + 4
后缀表达式:4 3 +
注:
中缀表达式虽然易读,但是计算机处理起来稍微有点麻烦(比如:括号的处理),不如 前缀、后缀 处理方便(消除了括号)。
所以一般处理表达式时 会对表达式进行转换,比如:中缀表达式转为后缀表达式,然后再对 后缀表达式进行处理。
中缀转后缀、中缀转前缀 过程类似,需要注意的是(详细可见下面转换步骤):
中缀转前缀时,从右至左扫描字符串,且遇到右括号 ")" 直接入栈。
中缀转后缀时,从左至右扫描字符串,且遇到左括号 "(" 直接入栈。
(2)前缀表达式 以及 中缀 转 前缀
【前缀(波兰)表达式:】 基本概念: 前缀表达式又称为 波兰表达式,其运算符(+、-、*、/)位于操作数前。 举例: 一个表达式为:(3 + 4) * 5 - 6,其 对应的前缀表达式为 - * + 3 4 5 6。 如何处理前缀表达式: Step1:需要一个栈来存储操作数,从右至左扫描表达式。 Step1.1:如果扫描的是数字,那么就将数字入栈, Step1.2:如果扫描的是字符(+、-、*、/),就弹出栈顶值两次,并通过运算符进行计算,最后将结果再次入栈。 Step2:重复 Step1 过程直至 表达式扫描完成,最后栈中的值即为 表达式结果。 如何处理前缀表达式(- * + 3 4 5 6): Step1:从右至左扫描,依次将 6 5 4 3 入栈。此时栈元素为 6 5 4 3。 Step1.1:扫描到 +,弹出栈顶值 3、4,相加(4 + 3 = 7)并入栈,即 此时栈元素为 6 5 7。 Step1.2:扫描到 *,弹出栈顶值 7、5,相乘(5 * 7 = 35)并入栈,即 此时栈元素为 6 35。 Step1.3:扫描到 -,弹出栈顶值 6、35,相减(35 - 6 = 29)并入栈,即 此时栈元素为 29。 【中缀表达式 转换为 前缀表达式:】 中缀表达式转前缀表达式步骤: Step1:初始化两个栈 A、B,A 用于记录 运算符、B 用于记录 中间结果。 Step2:从右至左扫描 中缀表达式。 Step2.1:如果扫描的是数字,直接将其压入栈 B。 Step2.2:如果扫描的是运算符(+、-、*、/),则比较当前运算符 与 A 栈顶运算符 的优先级。 Step2.2.1:若 A 为空 或者 栈顶运算符为右括号 ")",则当前运算符 直接入栈。 Step2.2.2:若上面条件不满足,则比较优先级,若当前运算符优先级 比 A 栈顶运算符 优先级高,则当前运算符 也入栈。 Step2.2.3:若上面条件不满足,即当前运算符优先级低,则将 A 栈顶运算符弹出并压入 B 栈。重新执行 Step2.2 进行运算符比较。 Step2.3:如果扫描的是括号 Step2.3.1:如果为右括号 ")",则直接压入 A 栈。 Step2.3.2:如果为左括号 "(",则依次弹出 A 栈顶元素并压入 B 栈,直至遇到 右括号 ")",此时 这对括号可以 舍弃。 Step2.4:重复上面扫描步骤,直至表达式扫描完成。 Step3:将 A 栈中剩余元素依次取出并压入 B 栈。 Step4:此时 B 栈顺序取出结果即为前缀表达式。 中缀表达式 "(3 + 4) * 5 - 6" 如何 转为前缀表达式 "- * + 3 4 5 6": Step1:初始化两个栈 A、B。A 存储运算符,B 存储中间结果。从右到左扫描中缀表达式。 Step1.1:扫描到 6,直接存入 B 栈,此时 A 栈元素为 空,B 栈元素为 6。 Step1.2:扫描到 -,此时 A 栈为空,直接存入 A 栈,此时 A 栈元素为 -,B 栈元素为 6。 Step1.3:扫描到 5,直接存入 B 栈,此时 A 栈元素为 -,B 栈元素为 6 5。 Step1.4:扫描到 *,当前运算符 * 比 A 栈顶运算符 优先级高,直接入栈,即此时 A 栈元素为 - *,B 栈元素为 6 5。 Step1.5:扫描到 ),直接入 A 栈,此时 A 栈元素为 - * ),B 栈元素为 6 5。 Step1.6:扫描到 4,直接存入 B 栈,此时 A 栈元素为 - * ),B 栈元素为 6 5 4。 Step1.7:扫描到 +,由于栈顶元素为右括号 ")",直接入 A 栈,此时 A 栈元素为 - * ) +,B 栈元素为 6 5 4。 Step1.8:扫描到 3,直接入 B 栈,此时 A 栈元素为 - * ) +,B 栈元素为 6 5 4 3。 Step1.9:扫描到左括号 "(",A 栈顶元素出栈并压入 B 栈直至遇到 右括号 ")",且移除括号,此时 A 栈元素为 - *, B 栈元素为 6 5 4 3 +。 Step2:将 A 栈剩余元素依次取出并压入 B 栈。此时 A 栈为空,B 栈元素为 6 5 4 3 + * -。 Step3:将 B 依次取出即为前缀表达式 "- * + 3 4 5 6"。
(3)中缀表达式
【中缀表达式:】 基本概念: 中缀表达式就是最常见的运算表达式,其运算符在操作数中间。 注: 中缀表达式括号不可省,其用于表示运算的优先顺序。 举例: 一个表达式为:(3 + 4) * 5 - 6,这就是中缀表达式。 如何处理中缀表达式: Step1:需要两个栈 A、B,A 用于存放 操作数,B 用于存放 符号(运算符、括号)。 Step2:从左到右扫描 中缀表达式。 Step2.1:如果扫描的是 数字,则直接压入 A 栈。 Step2.2:如果扫描的是 运算符(+、-、*、/),则比较当前运算符 与 B 栈顶运算符 的优先级。 Step2.2.1:若 B 为空 或者 栈顶元素为左括号 "(",则当前运算符直接入栈。 Step2.2.2:若上面条件不满足,则比较优先级,若当前运算符 比 B 栈顶运算符 优先级高,则当前运算符 入 B 栈。 Step2.2.3:若上面条件不满足,即当前运算符优先级低,则将 B 栈顶运算符弹出,并弹出 A 栈顶两个数据进行 计算,最后将计算结果存入 A 栈。重新执行 Step2.2 进行运算符比较。 Step2.3:如果扫描的是括号: Step2.3.1:若为左括号 "(",则直接压入 B 栈。 Step2.3.2:若为右括号 ")",则依次弹出 B 栈运算符直至遇到左括号 "(",B 栈每取一个元素,A 栈取两个元素,计算后将结果重新压入 A 栈。 Step2.4:重复上面扫描步骤,直至表达式扫描完成。 Step3:依次取出 B 栈顶运算符 以及 A 栈顶元素 计算,最后结果即为 表达式结果。 注: 直接处理中缀表达式,在于其会直接通过 运算符 进行运算。 如何处理中缀表达式 "(3 + 4) * 5 - 6": Step1:初始化两个栈 A、B。A 用于记录 操作数, B 用于记录 运算符。 Step2:从左至右扫描 中缀表达式。 Step2.1:扫描到左括号 "(",直接入 B 栈,此时 A 栈元素为空,B 栈元素为 (。 Step2.2:扫描到 3,直接入 A 栈,此时 A 栈元素为 3,B 栈元素为 (。 Step2.3:扫描到 +,此时 B 栈顶元素为左括号 "(",直接入 B 栈,此时 A 栈元素为 3,B 栈元素为 ( +。 Step2.4:扫描到 4,直接入 A 栈,此时 A 栈元素为 4,B 栈元素为 ( +。 Step2.5:扫描到右括号 ")",B 栈顶元素 + 出栈,A 栈弹出 4、 3,计算后重新压入 A 栈, B 继续弹出栈顶元素为左括号 "(",直接将其出栈。此时 A 栈元素为 7,B 栈元素为空。 Step2.6:扫描到 *,B 栈元素为空,直接入 B 栈,此时 A 栈元素为 7,B 栈元素为 *。 Step2.7:扫描到 5,直接入 A 栈,此时 A 栈元素为 7 5,B 栈元素为 *。 Step2.8:扫描到 -,当前运算符 - 比 B 栈顶运算符优先级 低,B 栈顶运算符出栈,A 栈弹出 5、7,计算后压入 A 栈, 此时 B 栈为空,当前运算符直接压入 B 栈,即此时 A 栈元素为 35,B 栈元素为 -。 Step2.9:扫描到 6,直接入 A 栈,此时 A 栈元素为 35 6, B 栈元素为 -。 Step3:取出 B 栈顶元素 -,A 栈弹出元素 6、35,计算后压入 A 栈,此时 B 栈为空,即表达式计算结束,A 栈最终结果即为表达式结果,即 29。
(4)后缀表达式 以及 中缀 转 后缀
【后缀(逆波兰)表达式:】 基本概念: 后缀表达式又称为 逆波兰表达式,其运算符位于操作数之后。 举例: 一个表达式为:(3 + 4) * 5 - 6,其 对应的前缀表达式为:3 4 + 5 * 6 - 如何处理后缀表达式: Step1:需要一个栈来存储操作数,从左至右扫描表达式。 Step1.1:如果扫描的是数字,那么就将数字入栈, Step1.2:如果扫描的是字符(+、-、*、/),就弹出栈顶值两次,并通过运算符进行计算,最后将结果再次入栈。 Step2:重复 Step1 过程直至 表达式扫描完成,最后栈中的值即为 表达式结果。 如何处理后缀表达式(3 4 + 5 * 6 -): Step1:从左至右扫描,依次将 3 4 入栈。此时栈元素为 3 4。 Step1.1:扫描到 +,弹出栈顶值 3、4,相加并入栈,即 此时栈元素为 7。 Step1.2:扫描到 5,入栈,即 此时栈元素为 7 5。 Step1.3:扫描到 *,弹出栈顶值 5、7,相乘并入栈,即 此时栈元素为 35。 Step1.4:扫描到 6,入栈,即 此时栈元素为 35 6。 Step1.5:扫描到 -,弹出栈顶值 6、35,相减并入栈,即 此时栈元素为 29。 【中缀表达式 转换为 后缀表达式:】 中缀表达式转后缀表达式步骤: Step1:初始化两个栈 A、B,A 用于记录 运算符、B 用于记录 中间结果。 Step2:从左至右扫描 中缀表达式。 Step2.1:如果扫描的是数字,直接将其压入栈 B。 Step2.2:如果扫描的是运算符(+、-、*、/),则比较当前运算符 与 A 栈顶运算符 的优先级。 Step2.2.1:若 A 为空 或者 栈顶运算符为左括号 "(",则当前运算符 直接入栈。 Step2.2.2:若上面条件不满足,则比较优先级,若当前运算符优先级 比 A 栈顶运算符 优先级高,则当前运算符 也入栈。 Step2.2.3:若上面条件不满足,即当前运算符优先级低,则将 A 栈顶运算符弹出并压入 B 栈。重新执行 Step2.2 进行运算符比较。 Step2.3:如果扫描的是括号 Step2.3.1:如果为左括号 "(",则直接压入 A 栈。 Step2.3.2:如果为右括号 ")",则依次弹出 A 栈顶元素并压入 B 栈,直至遇到 左括号 "(",此时 这对括号可以 舍弃。 Step2.4:重复上面扫描步骤,直至表达式扫描完成。 Step3:将 A 栈中剩余元素依次取出并压入 B 栈。 Step4:此时 B 栈逆序结果即为后缀表达式。 注: 实际写代码时,由于 B 栈自始至终不会进行弹出操作,且其结果的 逆序 才是 后缀表达式。 所以为了减少一次 逆序 的过程,可以直接使用 数组 或者 链表 进行存储,然后 顺序读取即可。 中缀表达式 "(3 + 4) * 5 - 6" 如何 转为后缀表达式 "3 4 + 5 * 6 -": Step1:初始化两个栈 A、B。A 存储运算符,B 存储中间结果。从左至右扫描中缀表达式。 Step1.1:扫描到左括号 "(",压入 A 栈,此时 A 栈元素为 (,B 栈元素为空。 Step1.2:扫描到 3,压入 B 栈,此时 A 栈元素为 (,B 栈元素为 3。 Step1.3:扫描到 +,由于 A 栈顶元素为左括号 "(",所以直接入栈。此时 A 栈元素为 ( +,B 栈元素为 3。 Step1.4:扫描到 4,压入 B 栈,此时 A 栈元素为 ( +,B 栈元素为 3 4。 Step1.5:扫描到右括号 ),A 栈元素依次出栈压入 B 直至遇到左括号 "(",并移除括号。此时 A 栈元素为 空,B 栈元素为 3 4 +。 Step1.6:扫描到 *,由于 A 栈为空直接入栈,此时 A 栈元素为 *,B 栈元素为 3 4 +。 Step1.7:扫描到 5,压入 B 栈,A 栈元素为 *,B 栈元素为 3 4 + 5。 Step1.8:扫描到 -,当前运算符 - 优先级低于 A 优先级,所以 A 栈顶元素弹出并压入 B 栈,此时 A 栈为空,当前运算符直接存入。此时 A 栈元素为 -,B 栈元素为 3 4 + 5 *。 Step1.9:扫描到 6,压入 B 栈,此时 A 栈元素为 -,B 栈元素为 3 4 + 5 * 6。 Step2:将 A 剩余元素出栈并压入 B。此时 A 栈为空,B 栈元素为 3 4 + 5 * 6 -。 Step3:将 B 栈元素依次取出并倒序输出,即为 后缀表达式 "3 4 + 5 * 6 -"。
(5)中缀表达式、前缀表达式、后缀表达式代码实现
如下代码,实现 基本表达式(多位数且带括号)的 +、-、*、/。
此处直接使用 Stack 类作为 栈 使用,不使用自定义栈结构。
【代码实现:】 package com.lyh.stack; import java.util.ArrayList; import java.util.List; import java.util.Stack; public class Expression { public static void main(String[] args) { Expression expressionDemo = new Expression(); // 定义一个表达式(默认格式正确,此处不做过多的格式校验) // String expression = ("2+3*(7-4)+8/4").trim(); String expression = ("(13-6)*5-6").trim(); System.out.println("当前表达式为: " + expression); System.out.println("================================"); List<String> infixExpressionList = expressionDemo.transfor(expression); System.out.println("表达式转换后为中缀表达式: " + infixExpressionList); System.out.println("================================"); System.out.println("中缀表达式求值为: " + expressionDemo.infixExpression(infixExpressionList)); System.out.println("================================"); List<String> prefixExpressionList = expressionDemo.infixToPrefix(infixExpressionList); System.out.println("中缀表达式: " + infixExpressionList + " 转为 前缀表达式: " + prefixExpressionList); System.out.println("前缀表达式求值为: " + expressionDemo.prefixExpression(prefixExpressionList)); System.out.println("================================"); List<String> suffixExpressionList = expressionDemo.infixToSuffix(infixExpressionList); System.out.println("中缀表达式: " + infixExpressionList + " 转为 后缀表达式: " + suffixExpressionList); System.out.println("后缀表达式求值为: " + expressionDemo.suffixExpression(suffixExpressionList)); System.out.println("================================"); } /** * 字符串转换成集合保存,便于操作 * @param expression 待转换的表达式 * @return 转换完成的表达式 */ public List<String> transfor(String expression) { // 用于保存最终结果 List<String> result = new ArrayList<>(); // 用于转换多位数 String temp = ""; // 遍历字符串,将其 数据取出(可能存在多位数) 挨个存入集合 for(int i = 0; i < expression.length(); i++) { // 遇到多位数,就使用 temp 拼接 while(i < expression.length() && expression.charAt(i) >= '0' && expression.charAt(i) <= '9') { temp += expression.charAt(i); i++; } // 将多位数存放到集合中 if (temp != "") { result.add(temp); temp = ""; } // 存放符号(+、-、*、/、括号) if (i < expression.length()) { result.add(String.valueOf(expression.charAt(i))); } } return result; } /** * 中缀表达式求值(从左到右扫描表达式) * @param expression 表达式 * @return 计算结果 */ public String infixExpression(List<String> expression) { Stack<String> stackA = new Stack<>(); // 用于存放操作数,简称 A 栈 Stack<String> stackB = new Stack<>(); // 用于存放运算符,简称 B 栈 // 遍历集合,取出表达式中 数据 以及 运算符 存入栈中并计算 expression.forEach(x -> { // 如果取出的是数据,直接存放进 A 栈 if (x.matches("\\d+")) { stackA.push(x); } else { // 如果当前运算符为右括号 ")" if (")".equals(x)) { // 依次取出 B 栈顶运算符 以及 A 栈顶两个元素进行计算,计算结果再存入 A 栈,直至遇到左括号 "(" while(stackB.size() > 0 && !"(".equals(stackB.peek())) { stackA.push(calculate(stackA.pop(), stackA.pop(), stackB.pop())); } // 移除左括号 "(" 与 当前运算符右括号 ")",即此次比较结束。 stackB.pop(); } else { // 比较运算符优先级,判断当前运算符是直接进入 B 栈,还是先取出优先级高的运算符计算后、再将当前运算符入栈。 while(true) { // 如果 当前运算符为左括号 "(" 或者 B 栈为空 或者 B 栈顶元素为 左括号 "(" 或者 当前运算符优先级 高于 B 栈顶元素优先级,则当前运算符直接入栈 if ("(".equals(x) || stackB.size() == 0 || "(".equals(stackB.peek()) || priority(x) > priority(stackB.peek())) { stackB.push(x); break; } // 以上条件均不满足,即当前运算符优先级 小于等于 B 栈顶元素优先级 // if (priority(x) <= priority(stackB.peek())) { // 依次取出 B 栈顶运算符 以及 A 栈顶两个元素进行计算,计算结果再存入 A 栈 stackA.push(calculate(stackA.pop(), stackA.pop(), stackB.pop())); // } } } } }); // 依次取出 B 栈顶运算符 以及 A 栈顶两个元素进行计算,计算结果再存入 A 栈 while(stackB.size() > 0) { stackA.push(calculate(stackA.pop(), stackA.pop(), stackB.pop())); } return stackA.pop(); } /** * 返回运算符优先级 * @param operator 运算符 * @return 优先级(0 ~ n, 0 为最小优先级) */ public int priority(String operator) { switch (operator) { case "+": return 1; case "-": return 1; case "*": return 2; case "/": return 2; default: return 0; } } /** * 根据运算符 计算 两数据,并返回计算结果 * @param num 数据 A * @param num2 数据 B * @param operator 运算符 * @return 计算结果 */ public String calculate(String num, String num2, String operator) { String result = ""; switch (operator) { case "+": result = String.valueOf(Integer.valueOf(num2) + Integer.valueOf(num)); break; case "-": result = String.valueOf(Integer.valueOf(num2) - Integer.valueOf(num)); break; case "*": result = String.valueOf(Integer.valueOf(num2) * Integer.valueOf(num)); break; case "/": result = String.valueOf(Integer.valueOf(num2) / Integer.valueOf(num)); break; default: result = ""; break; } return result; } /** * 前缀表达式求值(从右到左扫描表达式) * @param expression 前缀表达式 * @return 计算结果 */ public String prefixExpression(List<String> expression) { Stack<String> stackA = new Stack<>(); // 用于存储操作数,简称 A 栈 // 从右到左扫描表达式 for (int i = expression.size() - 1; i >= 0; i--) { // 用于保存当前表达式数据(操作数 或者 运算符) String temp = expression.get(i); // 如果当前数据为 操作数,则直接存入 A 栈 if (temp.matches("\\d+")) { stackA.push(temp); } else { // 若为运算符,则依次弹出 A 栈顶两个数据,并根据运算符进行计算,计算结果重新存入 A 栈 // 此处顺序要注意,与后缀有区别 String num2 = stackA.pop(); String num = stackA.pop(); stackA.push(calculate(num, num2, temp)); } } // 扫描结束后,A 栈最终结果即为 表达式结果 return stackA.pop(); } /** * 中缀表达式转前缀表达式(从右到左扫描表达式) * @param expression 中缀表达式 * @return 前缀表达式 */ public List<String> infixToPrefix(List<String> expression) { Stack<String> stackA = new Stack<>(); // 用于保存 操作符(运算符),简称 A 栈 Stack<String> stackB = new Stack<>(); // 用于保存 中间结果(存储数据以及运算符,存储过程中不会有出栈操作),简称 B 栈 List<String> result = new ArrayList<>(); // 用于记录最终结果 // 从右到左扫描表达式,取出数据、运算符 并计算 for (int i = expression.size() - 1; i >= 0; i--) { // 用于表示集合当前取出的数据 String temp = expression.get(i); // 如果取出的为 操作数,直接存入 B 栈 if (temp.matches("\\d+")) { stackB.push(temp); } else { // 如果取出的是左括号 if ("(".equals(temp)) { // 依次弹出 A 栈顶元素并压入 B 栈,直至遇到 右括号 ")" while(stackA.size() > 0 && !")".equals(stackA.peek())) { stackB.push(stackA.pop()); } // 移除 A 栈顶右括号 ")" stackA.pop(); } else { // 比较运算符优先级,判断运算符直接进入 A 栈 还是 先弹出 A 栈顶元素并压入 B 栈后、再将当前运算符入 A 栈 while(true) { // 如果当前运算符为右括号 ")" 或者 A 栈为空 或者 A 栈顶元素为右括号 ")" 或者 当前运算符优先级 高于 A 栈顶运算符,则直接入 A 栈 if (")".equals(temp) || stackA.size() == 0 || ")".equals(stackA.peek()) || priority(temp) > priority(stackA.peek())) { stackA.push(temp); break; } // 若上面条件均不满足,即当前运算符优先级小于等于 A 栈顶运算符,则弹出 A 栈顶运算符并压入 B 栈 stackB.push(stackA.pop()); } } } } // 依次将 A 栈剩余元素弹出并压入到 B 栈 while(stackA.size() > 0) { stackB.push(stackA.pop()); } // 依次取出 B 栈元素,即为 前缀表达式 while(stackB.size() > 0) { result.add(stackB.pop()); } return result; } /** * 中缀表达式转后缀表达式(从左到右扫描表达式) * @param expression 中缀表达式 * @return 后缀表达式 */ public List<String> infixToSuffix(List<String> expression) { Stack<String> stackA = new Stack<>(); // 用于保存 操作符(运算符),简称 A 栈 // Stack<String> stackB = new Stack<>(); // 用于保存 中间结果,简称 B 栈 // 由于 B 栈反序输出才是后缀表达式,此处可以直接存放在 集合中,顺序读取即为 后缀表达式。 List<String> result = new ArrayList<>(); // 用于保存 最终结果,此处用来替代 B 栈,后面简称 B 栈。 // 从左到右扫描后缀表达式 expression.forEach(x -> { // 如果取出的是 操作数,直接存入 B 栈 if (x.matches("\\d+")) { result.add(x); } else { // 如果操作符是右括号 ")" if (")".equals(x)) { // 依次将 A 栈顶运算符弹出 并压入 B 栈,直至遇到左括号 "(" while(stackA.size() > 0 && !"(".equals(stackA.peek())) { result.add(stackA.pop()); } // 移除 A 栈顶左括号 "(" stackA.pop(); } else { // 比较运算符优先级,判断运算符直接进入 A 栈 还是 先弹出 A 栈顶元素并压入 B 栈后、再将当前运算符入 A 栈 while(true) { // 如果当前运算符为左括号 "(" 或者 A 栈为空 或者 A 栈顶运算符为左括号 "(" 或者 当前运算符优先级 高于 A 栈顶运算符,则直接入 A 栈 if ("(".equals(x) || stackA.size() == 0 || "(".equals(stackA.peek()) || priority(x) > priority(stackA.peek())) { stackA.push(x); break; } // 如果上面条件均不满足,即当前运算符 优先级 小于或等于 A 栈顶运算符 // 则将 A 栈顶运算符取出并 放入 B 栈 result.add(stackA.pop()); } } } }); // 依次将 A 栈顶运算符取出放入 B 栈 while(stackA.size() > 0) { result.add(stackA.pop()); } return result; } /** * 后缀表达式求值(从左到右扫描表达式) * @param expression 后缀表达式 * @return 计算结果 */ public String suffixExpression(List<String> expression) { Stack<String> stackA = new Stack<>(); // 用于保存 操作数,简称 A 栈 // 从左到右扫描表达式 expression.forEach(x -> { // 如果是 数字,直接进 A 栈 if (x.matches("\\d+")) { stackA.push(x); } else { // 是运算符,则取出 A 栈顶两元素,并计算,将计算结果重新压入 A 栈 stackA.push(calculate(stackA.pop(), stackA.pop(), x)); } }); // 扫描结束后,A 栈最终结果即为 表达式结果 return stackA.pop(); } } 【输出结果:】 当前表达式为: (13-6)*5-6 ================================ 表达式转换后为中缀表达式: [(, 13, -, 6, ), *, 5, -, 6] ================================ 中缀表达式求值为: 29 ================================ 中缀表达式: [(, 13, -, 6, ), *, 5, -, 6] 转为 前缀表达式: [-, *, -, 13, 6, 5, 6] 前缀表达式求值为: 29 ================================ 中缀表达式: [(, 13, -, 6, ), *, 5, -, 6] 转为 后缀表达式: [13, 6, -, 5, *, 6, -] 后缀表达式求值为: 29 ================================
7、递归与回溯、八皇后问题
(1)递归:
递归指的是 方法调用自身方法去解决问题的过程。
其目的是 将一个复杂的大问题 转换为 与原问题类似的小问题去求解。递归必须得有结束条件,否则将会陷入无限递归(导致栈溢出异常)。
常用场景:快排、归并排序、二分查找、汉诺塔、八皇后 等问题。
(2)回溯:
回溯指的是 类似枚举的选优搜索过程,当条件不符合时,返回上一层(即回溯)重新判断。
其解决的是 某种场景下有许多个解,依次判断每个解是否合适,如果不合适就回退到上一层,重新判断下一个解是否合适。
常见场景:八皇后 问题。
(3)八皇后问题分析
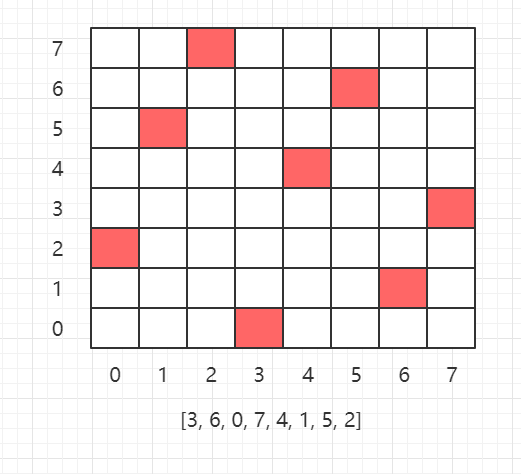
【八皇后问题介绍:】 在一个 8 * 8 的国际象棋棋盘上,摆放 八个皇后,且皇后之间不能相互攻击,总共有多少种摆法。 不能相互攻击 即: 任意两个皇后 不能同时 处在 同一行、同一列、同一斜线上。 【思路分析:】 采用 回溯 方法解决。 每次放置皇后时,均从每行的第一列开始尝试,并校验该皇后位置是否与其他皇后位置发生冲突,如果不冲突则递归调用下一个皇后进行放置, 如果冲突则尝试当前皇后位置的下一个位置是否能够放置,若当前皇后在当前行的所有列均放置失败,则回溯到上一个皇后所处位置,使上一个皇后放置在其下一列 并重新判断该位置是否冲突。 即: Step1:第一个皇后放在第一行第一列。 Step2:第二个皇后放在第二行第一列,判断是否会攻击,如果会攻击,则将 第二个皇后放在第二行第二列 进行判断。 若仍会攻击,则依次放置下去,直至第二行第八列。若仍会攻击,则后续不用执行(此时第二个皇后 8 个位置均放置失败),回溯到 上一行 并再次枚举。 Step3:第二个皇后放好后,同理放置第三个皇后 直至 放置第八个 皇后,若均不冲突则 为一个解。 【判断皇后之间是否攻击:】 使用一维数组 a[8] 存储可行的 八皇后 放置位置(二维数组亦可)。 每一个数组元素存储范围为 0~7,分别表示第 1 ~ 8 位置。 判断皇后之间是否攻击:设当前为第 n 个皇后,记为 a[n]。 同一行:不需要考虑,每次都是不同行。 同一列:遍历一维数组,如果 a[i] == a[n],则表示当前存在攻击。 for(int i = 0; i < n; i++) { if (a[i] == a[n]) { return false; } } 同一斜线:遍历一维数组,若 Math.abs(n - i) == Math.abs(a[n] - a[i]),则存在攻击。 for(int i = 0; i < n; i++) { if (Math.abs(n - i) == Math.abs(a[n] - a[i])) { return false; } } 注: i 指的是第 i+1 个皇后,a[i] 指的是第 i+1 个皇后所占据的位置(0~7)。 所以 a[i] == a[n] 时表示同一列。 Math.abs(n - i) == Math.abs(a[n] - a[i]) 表示同一斜线(看成等腰直角三角形)。

【八皇后代码实现:】 package com.lyh.recursion; import java.util.Arrays; public class EightQueens { private int maxsize = 8; // 定义最大为 8 皇后 private int count = 0; // 用于记录皇后放置总解法数 private int[] arrays = new int[maxsize]; // 用于存储 8 皇后的解法,范围为 0 ~ 7,表示第 1 ~ 8 位置 public EightQueens() { } public EightQueens(int maxsize) { this.maxsize = maxsize; arrays = new int[this.maxsize]; } public static void main(String[] args) { EightQueens eightQueens = new EightQueens(); eightQueens.putQueen(0); System.out.println("总解法: " + eightQueens.count); } /** * 检查当前皇后的放置位置 是否 与其他皇后位置冲突 * @param n 当前为第 n+1 皇后 * @return true 表示不冲突 */ public boolean check(int n) { // 遍历当前所有皇后,已放置 0 ~ n-1 个皇后,即 第 1 ~ n 皇后位置 for(int i = 0; i < n; i++) { // arrays[i] == arrays[n] 表示两皇后在同一列 // Math.abs(n - i) == Math.abs(arrays[n] - arrays[i]) 表示两皇后在同一斜线上(看成等腰直角三角形处理) if (arrays[i] == arrays[n] || Math.abs(n - i) == Math.abs(arrays[n] - arrays[i])) { return false; } } return true; } /** * 递归 + 回溯 放置皇后 * @param n 第 n+1 个皇后 */ public void putQueen(int n) { // 所有皇后放置完成,打印皇后放置方法 // 此处为第一个出口,即 8 个皇后全部放置完成时。 if (n == maxsize) { System.out.println(Arrays.toString(arrays)); count++; return; } // 枚举依次求解,遍历 0 ~ maxsize - 1,表示当前皇后放置在第 1 ~ maxsize 个位置。 // 此处为第二个出口,若遍历完成,n 仍不为 8,即 第 n-1 个皇后 8 个位置均放置失败,后续无需再做,回溯到上一个皇后放置位置的下一个位置 for (int i = 0; i < maxsize; i++) { // 放置皇后 arrays[n] = i; // 当前皇后放置不冲突,则放置下一个皇后,若冲突则结束当前循环并判断下一个位置是否冲突 if (check(n)) { putQueen(n + 1); } } } } 【输出结果:】 [0, 4, 7, 5, 2, 6, 1, 3] [0, 5, 7, 2, 6, 3, 1, 4] [0, 6, 3, 5, 7, 1, 4, 2] [0, 6, 4, 7, 1, 3, 5, 2] [1, 3, 5, 7, 2, 0, 6, 4] [1, 4, 6, 0, 2, 7, 5, 3] [1, 4, 6, 3, 0, 7, 5, 2] [1, 5, 0, 6, 3, 7, 2, 4] [1, 5, 7, 2, 0, 3, 6, 4] [1, 6, 2, 5, 7, 4, 0, 3] [1, 6, 4, 7, 0, 3, 5, 2] [1, 7, 5, 0, 2, 4, 6, 3] [2, 0, 6, 4, 7, 1, 3, 5] [2, 4, 1, 7, 0, 6, 3, 5] [2, 4, 1, 7, 5, 3, 6, 0] [2, 4, 6, 0, 3, 1, 7, 5] [2, 4, 7, 3, 0, 6, 1, 5] [2, 5, 1, 4, 7, 0, 6, 3] [2, 5, 1, 6, 0, 3, 7, 4] [2, 5, 1, 6, 4, 0, 7, 3] [2, 5, 3, 0, 7, 4, 6, 1] [2, 5, 3, 1, 7, 4, 6, 0] [2, 5, 7, 0, 3, 6, 4, 1] [2, 5, 7, 0, 4, 6, 1, 3] [2, 5, 7, 1, 3, 0, 6, 4] [2, 6, 1, 7, 4, 0, 3, 5] [2, 6, 1, 7, 5, 3, 0, 4] [2, 7, 3, 6, 0, 5, 1, 4] [3, 0, 4, 7, 1, 6, 2, 5] [3, 0, 4, 7, 5, 2, 6, 1] [3, 1, 4, 7, 5, 0, 2, 6] [3, 1, 6, 2, 5, 7, 0, 4] [3, 1, 6, 2, 5, 7, 4, 0] [3, 1, 6, 4, 0, 7, 5, 2] [3, 1, 7, 4, 6, 0, 2, 5] [3, 1, 7, 5, 0, 2, 4, 6] [3, 5, 0, 4, 1, 7, 2, 6] [3, 5, 7, 1, 6, 0, 2, 4] [3, 5, 7, 2, 0, 6, 4, 1] [3, 6, 0, 7, 4, 1, 5, 2] [3, 6, 2, 7, 1, 4, 0, 5] [3, 6, 4, 1, 5, 0, 2, 7] [3, 6, 4, 2, 0, 5, 7, 1] [3, 7, 0, 2, 5, 1, 6, 4] [3, 7, 0, 4, 6, 1, 5, 2] [3, 7, 4, 2, 0, 6, 1, 5] [4, 0, 3, 5, 7, 1, 6, 2] [4, 0, 7, 3, 1, 6, 2, 5] [4, 0, 7, 5, 2, 6, 1, 3] [4, 1, 3, 5, 7, 2, 0, 6] [4, 1, 3, 6, 2, 7, 5, 0] [4, 1, 5, 0, 6, 3, 7, 2] [4, 1, 7, 0, 3, 6, 2, 5] [4, 2, 0, 5, 7, 1, 3, 6] [4, 2, 0, 6, 1, 7, 5, 3] [4, 2, 7, 3, 6, 0, 5, 1] [4, 6, 0, 2, 7, 5, 3, 1] [4, 6, 0, 3, 1, 7, 5, 2] [4, 6, 1, 3, 7, 0, 2, 5] [4, 6, 1, 5, 2, 0, 3, 7] [4, 6, 1, 5, 2, 0, 7, 3] [4, 6, 3, 0, 2, 7, 5, 1] [4, 7, 3, 0, 2, 5, 1, 6] [4, 7, 3, 0, 6, 1, 5, 2] [5, 0, 4, 1, 7, 2, 6, 3] [5, 1, 6, 0, 2, 4, 7, 3] [5, 1, 6, 0, 3, 7, 4, 2] [5, 2, 0, 6, 4, 7, 1, 3] [5, 2, 0, 7, 3, 1, 6, 4] [5, 2, 0, 7, 4, 1, 3, 6] [5, 2, 4, 6, 0, 3, 1, 7] [5, 2, 4, 7, 0, 3, 1, 6] [5, 2, 6, 1, 3, 7, 0, 4] [5, 2, 6, 1, 7, 4, 0, 3] [5, 2, 6, 3, 0, 7, 1, 4] [5, 3, 0, 4, 7, 1, 6, 2] [5, 3, 1, 7, 4, 6, 0, 2] [5, 3, 6, 0, 2, 4, 1, 7] [5, 3, 6, 0, 7, 1, 4, 2] [5, 7, 1, 3, 0, 6, 4, 2] [6, 0, 2, 7, 5, 3, 1, 4] [6, 1, 3, 0, 7, 4, 2, 5] [6, 1, 5, 2, 0, 3, 7, 4] [6, 2, 0, 5, 7, 4, 1, 3] [6, 2, 7, 1, 4, 0, 5, 3] [6, 3, 1, 4, 7, 0, 2, 5] [6, 3, 1, 7, 5, 0, 2, 4] [6, 4, 2, 0, 5, 7, 1, 3] [7, 1, 3, 0, 6, 4, 2, 5] [7, 1, 4, 2, 0, 6, 3, 5] [7, 2, 0, 5, 1, 4, 6, 3] [7, 3, 0, 2, 5, 1, 6, 4] 总解法: 92
三、排序算法
1、常见内排序
之前总结过一篇,此处不重复介绍,对其稍作补充说明。
详见:https://www.cnblogs.com/l-y-h/p/12391241.html
2、基数排序(Radix Sort)
(1)什么是基数排序?
基数排序是桶排序的扩展,其将 整数 按照 位数(个位、十位、百位等)进行划分,每次划分后将划分的结果存放到相应的桶中,最终达到排序的目的。
基数排序属于稳定排序。
【基数排序步骤:(此时无法处理负数)】 Step1:首先定义一个桶数组,编号为 0 ~ 9,分别表示用于存储符合 0 ~ 9 的数据。 且每个桶元素 又是一个数组,用于存储符合 0 ~ 9 的数据。 Step2:对于一组数据,从每个数的 个位 开始进行划分(个位范围为 0 ~ 9),将数据分别存储到 桶数组中。 然后遍历输出得到新的数组。 Step3:对于新的一组数据,从每个数的 十位 开始划分,进行 Step2 同样操作。 Step4:同理,处理 百位、千位,若一个数没有 百位、千位,则将其视为 0 处理。 注: 首先得获取当前数据中 最大数据 的位数,然后再进行 位数划分。 比如: 7 99 10 8 中最大数据为 两位数,需进行 个位、十位 划分。 45 123 34 中最大数据为 三位数,需进行 个位、十位、百位 划分。 【基数排序存在 负数 时处理:】 可以先找到 负数的最小值,然后将所有数据 整体加上 负数最小值的绝对值 加 1,记为 min = |负数最小值|, 即 让所有数据均变为 非负数,然后再去排序,最后将结果 再整体减去 min 即可。 注: 若 最大值、最小值 濒临极限时,可能会造成数据溢出(此时慎用)。 【给数据 arr {38, 65, 97, 76, 13, 27, 49} 排序,并按照从小到大的顺序输出】 Step1:首先定义一个 二维数组 a[10][arr.length] 表示桶,分别用于存储符合 0 ~ 9 的数据。 Step2:按照 个位 进行划分。 38 个位为 8,进入 a[8] 桶。 65 个位为 5,进入 a[5] 桶。 97 个位为 7,进入 a[7] 桶。 76 个位为 6,进入 a[6] 桶。 13 个位为 3,进入 a[3] 桶。 27 个位为 7,进入 a[7] 桶。 49 个位为 9,进入 a[9] 桶。 即: 0 1 2 3 13 4 5 65 6 76 7 97 27 8 38 9 49 依次取出桶中元素,存入新数组中。即 {13, 65, 76, 97, 27, 38, 49} Step3:根据新数组按照 十位 进行划分。 13 十位为 1,进入 a[1] 桶。 65 十位为 6,进入 a[6] 桶。 76 十位为 7,进入 a[7] 桶。 97 十位为 9,进入 a[9] 桶。 27 十位为 2,进入 a[2] 桶。 38 十位为 3,进入 a[3] 桶。 49 十位为 4,进入 a[4] 桶。 即: 0 1 13 2 27 3 38 4 49 5 6 65 7 76 8 9 97 依次取出桶中元素,存入新数组中。即 {13, 27, 38, 49, 65, 76, 97}
(2)代码实现
【代码实现:】 package com.lyh.sort; import java.util.Arrays; public class RadixSort { public static void main(String[] args) { int[] arrays = new int[]{38, 65, 97, 76, 13, 27, 49}; radixSort(arrays); System.out.println("===================="); // int[] arrays = new int[]{38, 65, 0, -1, 13, 27, 49}; int[] arrays2 = new int[]{38, 65, 0, -1, 13, 27, -10}; radixSort(arrays2); } /** * 基数排序(包括负数排序) * @param arrays 待排序数组 */ public static void radixSort(int[] arrays) { // 判断数组是否合法 if (arrays.length <= 0) { System.out.println("数据为空"); return; } // 获取当前数据中最大值、最小值 int max = arrays[0]; int min = arrays[0]; for (int array : arrays) { if (max < array) { max = array; } if (min > array) { min = array; } } // min 小于 0,即当前存在负数,则将所有数据 加上 min 的绝对值,使其变为非负数 if (min < 0) { for (int i = 0; i < arrays.length; i++) { arrays[i] -= min; } max -= min; } // 定义二维数组,用于表示 桶,存储数据,bucket[0] ~ bucket[9] 分别用于存储 0 ~ 9 的数据 int[][] bucket = new int[10][arrays.length]; // 定义一维数组,用于表示 每个桶存储 数据的个数,bucketCount[0] ~ bucketCount[9] 分别用于存储 bucket[0] ~ bucket[9] 中数据的个数 int[] bucketCount = new int[10]; // 获取当前 最大值 的位数,根据 位数 确定需要进行 几次 数据划分操作 int maxLength = (max + "").length(); // 根据位数,按照 个位、十位、百位、千位 的顺序进行划分 for (int i = 0, m = 1; i < maxLength; i++, m *= 10) { // 遍历数组,将数据划分到 桶中存储 for (int j = 0; j < arrays.length; j++) { int temp = arrays[j] / m % 10; // 获取 个位、十位、百位 的值 bucket[temp][bucketCount[temp]++] = arrays[j]; // 桶存储数据,相应的 bucketCount 也要加 1 } int index = 0; // 用于记录新数组最后一个值的索引 // 遍历桶,取出数据组成新的数组, k < bucketCount.length 或者 k < bucket[0].length 均可,都表示 10(0 ~ 9) for (int k = 0; k < bucketCount.length; k++) { // 当前桶存在数据时,取出数据存入数组中,并将该桶置空 // 此处只需将 bucketCount 相应位置置 0 即可(无需将 bucket 置空,每次存储数据时均会覆盖,尽管会存在无用值,但无影响) if (bucketCount[k] > 0) { // 将桶元素复制到新数组中 // 源数组 bucket[k], 开始位置 0, 目标数组 arrays,目标数组起始位置 index,复制源数组的数据个数 bucketCount[k] System.arraycopy(bucket[k],0, arrays, index, bucketCount[k]); index += bucketCount[k]; // 当前桶记录清空 bucketCount[k] = 0; } } System.out.println("第 " + (i + 1) + " 次划分结果: " + Arrays.toString(arrays)); } // 如果存在负数,则需要减去 相应的值 if (min < 0) { for (int i = 0; i < arrays.length; i++) { arrays[i] += min; } } System.out.println("最终排序结果为: " + Arrays.toString(arrays)); } } 【输出结果:】 第 1 次划分结果: [13, 65, 76, 97, 27, 38, 49] 第 2 次划分结果: [13, 27, 38, 49, 65, 76, 97] 最终排序结果为: [13, 27, 38, 49, 65, 76, 97] ==================== 第 1 次划分结果: [10, 0, 23, 75, 37, 48, 9] 第 2 次划分结果: [0, 9, 10, 23, 37, 48, 75] 最终排序结果为: [-10, -1, 0, 13, 27, 38, 65]
(3)分析:
若数据中出现相同的值,且向桶存放数据以及从桶取数据的过程中不会出现交换值的情况,故排序是稳定的。
每次均会遍历数据 n,且最大位数为 k,即 时间复杂度为 O(n*k)。
需要使用二维数组存储 桶元素,使用一维数组存储 桶存储元素个数,即空间复杂度为 O(10 * n + 10),即空间复杂度为 O(n)。
四、查找算法
1、顺序(线性)查找
(1)什么是 线性查找?
最简单直接的一种查找方式,基本思想是 对于待查找数据 key, 从数据的第一个记录开始,逐个 与 key 比较,若存在与 key 相同的值则查找成功,若不存在则查找失败。
(2)代码实现
【代码实现:】 package com.lyh.search; public class LinearSearch { public static void main(String[] args) { int[] arrays = new int[]{100, 40, 78, 24, 10, 16}; int key = 10; int index = linearSearch(arrays, key); if (index != -1) { System.out.println("查找成功,下标为: " + index); } else { System.out.println("查找失败"); } } /** * 顺序查找,返回元素下标 * @param arrays 待查找数组 * @param key 待查找数据 * @return 查找失败返回 -1,查找成功返回 0 ~ n-1 */ public static int linearSearch(int[] arrays, int key) { // 遍历数组,挨个匹配 for (int i = 0; i < arrays.length; i++) { if (arrays[i] == key) { return i; } } return -1; } } 【输出结果:】 查找成功,下标为: 4
(3)分析
顺序查找效率是比较低的,n 个数据最坏情况下需要比较 n 次,即时间复杂度为 O(n)。
2、二分(折半)查找
(1)什么是 折半查找?
是一个效率较高的查找方法。其要求必须采用 顺序存储结构 且 存储数据有序。
【基本实现思路:】 Step1:确定数组的中间下标。 middle = (left + right) / 2。将数据 分为左右两部分。 Step2:将待查找数据 key 与 中间元素 arrays[middle] 比较。 Step2.1:如果 key > arrays[middle],则说明要查找数据在 middle 下标右侧,需要在右侧数据进行查找(递归)。 Step2.2:如果 key < arrays[middle],则说明要查找数据在 middle 下标左侧,需要在左侧数据进行查找(递归)。 Step2.3:如果 key == arrays[middle],则说明查找成功。 上面递归结束条件: 查找成功,结束递归。 查找失败,即 left > right 时,退出递归。 【举例:】 在 {13, 27, 38, 49, 65, 76, 97} 中查找 key = 27。 第一次折半: left = 0, right = 6, middle = 3 即 a[left] = 13, a[right] = 97, a[middle] = 49。 由于待查找数据 key < a[middle],则从左侧剩余数据 {13, 27, 38, 49} 开始查找。 第二次折半: left = 0, right = 2, middle = 1 即 a[left] = 0, a[right] = 38, a[middle] = 27。 由于待查找数据 key == a[middle],则查找成功。
(2)代码实现
【代码实现:】 package com.lyh.search; public class BinarySearch { public static void main(String[] args) { int[] arrays = new int[]{13, 27, 38, 49, 65, 76, 97}; int key = 27; int index = binarySearch(arrays, 0, arrays.length - 1, key); if (index != -1) { System.out.println("查找成功,下标为: " + index); } else { System.out.println("查找失败"); } } /** * 折半查找,返回元素下标 * @param arrays 待查找数组 * @param left 最左侧下标 * @param right 最右侧下标 * @param key 待查找数据 * @return 查找失败返回 -1,查找成功返回元素下标 0 ~ n */ public static int binarySearch(int[] arrays, int left, int right, int key) { // 若 left > right,则表示查找失败 if (left <= right) { // 获取中间下标 int middle = (left + right) / 2; if (key == arrays[middle]) { return middle; } else if (key > arrays[middle]) { return binarySearch(arrays, middle + 1, right, key); } else { return binarySearch(arrays, left, middle - 1, key); } } return -1; } } 【输出结果:】 查找成功,下标为: 1
(3)分析:
每次查找数据均折半,设折半次数为 x,则 2^x = n,即折半次数为 x = logn,时间复杂度为 O(logn)。效率比顺序查找高。
3、插值查找
(1)什么是插值查找?
插值查找类似于 折半查找,其区别在于 中间节点 是自适应的。
采用自适应节点是为了 使 middle 值更靠近 key,从而 减少 key 比较次数。
【插值查找、折半查找区别:】 折半查找 求 middle: middle = (left + right) / 2 = left + (right - left) / 2. 插值查找 求 middle: middle = left + (right - left) * (key - a[left]) / (a[right] - a[left]). 即 使用 (key - a[left]) / (a[right] - a[left]) 去替换 1 / 2,可以在某种情况下提高查找效率。 对于数据量较大、且数据分布较均匀的 数据来说,使用 插值查找 速度较快(较少比较次数)。 注: 除法可能会遇到异常(java.lang.ArithmeticException: / by zero)。 【举例:】 对于 0 ~ 99 的数,查找 27, 若采用 折半查找,需要折半 5 次。 若采用 插值查找,需要折半 1 次。
(2)代码实现
【代码实现:】 package com.lyh.search; public class InsertionSearch { public static void main(String[] args) { int[] arrays = new int[100]; for(int i = 0; i < arrays.length; i++) { arrays[i] = i; } int key = 27; int index = insertionSearch(arrays, 0, arrays.length - 1, key); if (index != -1) { System.out.println("查找成功,下标为: " + index); } else { System.out.println("查找失败"); } } /** * 插值查找,返回元素下标 * @param arrays 待查找数组 * @param left 最左侧下标 * @param right 最右侧下标 * @param key 待查找数据 * @return 查找失败返回 -1,查找成功返回元素下标 0 ~ n */ public static int insertionSearch(int[] arrays, int left, int right, int key) { // 数据不符合时,退出递归 if (left > right || key > arrays[right] || key < arrays[left]) { return -1; } // 自适应节点 int middle = left + (right - left) * (key - arrays[left]) / (arrays[right] - arrays[left]); if (key == arrays[middle]) { return middle; } else if (key > arrays[middle]) { return insertionSearch(arrays, middle + 1, right, key); } else { return insertionSearch(arrays, left, middle + 1, key); } } } 【输出结果:】 查找成功,下标为: 27
4、斐波那契(黄金分割)查找
(1)什么是 斐波那契 查找?
斐波那契查找 与 折半查找、插值查找 类似,都是改变中间节点的位置。
此时的 中间节点 位于 黄金分割点 附近。
【黄金分割比例:】 黄金分割比例指 将一个整体分为两个部分,其中 较小部分 : 较大部分 = 较大部分 : 整体,且值约为 0.618,此比例称为黄金分割比例。 比如: 1 米长绳子,分为 0.618 与 0.382 两部分,则 0.382 :0.618 == 0.618 :1。 【斐波那契数列:】 斐波那契公式: f(1) = 1; f(2) = 1; f(n) = f(n - 1) + f(n - 2); n > 2 即:数列 {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...} 斐波那契数列两个相邻数的比例,近似于 0.618。 比如: 21 : 34 == 0.6176470588235294 : 1 34 : 55 == 0.6181818181818182 : 1 【斐波那契查找算法原理:】 如何求黄金分割点: 由于斐波那契数列公式为 f(n) = f(n - 1) + f(n - 2), 且 f(n -1 ) : f(n - 2) == 0.618。 想要使用 斐波那契处理 数据,即将数据按照 f(n-1) 与 f(n-2) 分成两部分即可。 比如:f(n) - 1 = (f(n - 1) - 1) + (f(n - 2) - 1 + 1); 分为 (f(n - 1) - 1) 与 (f(n - 2) - 1 + 1) 两部分。 此时 left + (f(n - 1) - 1) 即为黄金分割点 middle。 斐波那契查找: 其将一组数据长度 看成是 斐波那契数列 进行处理,若当前数据长度 不满足 斐波那契数列,则使用 最后一个元素将其补齐。 长度符合后,记新数组为 temp,根据 middle 计算出中间节点,并进行判断。 若 key > temp[middle],则需要在右侧进行递归判断,而此时右侧属于 f(n - 2) 部分,即 k = k - 2; 若 key < temp[middle],则需要在左侧进行递归判断,而此时左侧属于 f(n - 1) 部分,即 k = k - 1; 若 key == temp[middle],则查找成功。 【举例:】 在 {13, 27, 38, 49, 65, 76, 97} 中查找 key = 27。 Step1:补齐数据。 当前数据 arrays 长度为 7,而与之相近的斐波那契数列值为 8(f(n) = 8, n = 5),需要将其补齐。 即数据变为 temp = {13, 27, 38, 49, 65, 76, 97, 97}. Step2:开始第一次查找操作,中间节点 middle = left + (f(n - 1) - 1) left = 0,right = 7,n = 5,middle = 4, key < temp[middle],即下次在左侧 {13, 27, 38, 49} 进行查找(right = middle - 1 = 3)。 左侧部分等同于 f(n - 1) 区,所以 n 减 1, 即 n = 4。 Step3:开始第二次查找, left = 0, right = 3,n = 4, middle = 2 key < temp[middle],即下次在左侧 {13, 27} 进行查找(right = middle - 1 = 1)。 左侧部分等同于 f(n - 1) 区,所以 n 减 1, 即 n = 3。 Step3:开始第三次查找, left = 0, right = 1,n = 3, middle = 1 key == temp[middle],查找成功。
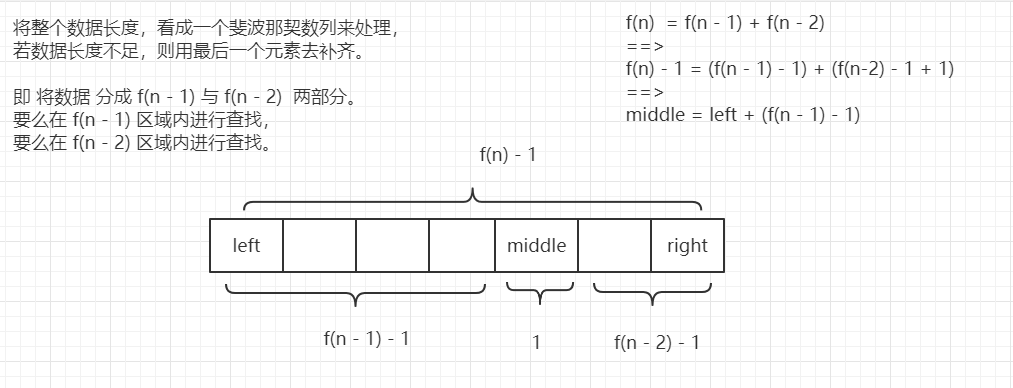
(2)代码实现
【代码实现:】 package com.lyh.search; import java.util.Arrays; public class FibonacciSearch { public static void main(String[] args) { int[] arrays = new int[]{13, 27, 38, 49, 65, 76, 97}; int key = 27; int index = fibonacciSearch(arrays, key); if (index != -1) { System.out.println("查找成功,当前下标为: " + index); } else { System.out.println("查找失败"); } } /** * 返回斐波那契数组(使用 迭代 实现) * @return 斐波那契数组 */ public static int[] fibonacci(int length) { if (length < 0) { return null; } int[] fib = new int[length]; if (length >= 1) { fib[0] = 1; } if (length >= 2) { fib[1] = 1; } for (int i = 2; i < length; i++) { fib[i] = fib[i - 1] + fib[i - 2]; } return fib; } /** * 斐波那契查找,返回对应数据下标 * 将数据长度看成 斐波那契数列,将数据分为 f(n - 1)、 f(n - 2) 两部分 * @param arrays 待查找数组 * @param key 待查找数据 * @return 查找失败返回 -1,查找成功返回相应的下标 */ public static int fibonacciSearch(int[] arrays, int key) { int n = 0; // 用于记录当前 分隔点 下标 int[] fibs = fibonacci(arrays.length); // 用于记录斐波那契数列 // 获取第一次分割点下标 while (arrays.length > fibs[n]) { n++; } // 若当前数组长度 不满足 斐波那契数列,则使用最后一个元素 去填充新数组,使新长度满足 斐波那契数列 int[] temp = Arrays.copyOf(arrays, fibs[n]); for (int i = arrays.length; i < fibs[n]; i++) { temp[i] = arrays[arrays.length - 1]; } // 开始查找 int left = 0; int right = temp.length - 1; while(left <= right) { // 获取中间节点,将数据区域分为 f(n - 1), f(n - 2) 两部分 int middle = left + fibs[n - 1] - 1; if (key == temp[middle]) { // 查找成功 return middle; } else if (key > temp[middle]) { // 当前查找失败,下次在右侧 f(n - 2) 区域进行查找 left = middle + 1; n -= 2; } else { // 当前查找失败,下次在左侧 f(n - 1) 区域进行查找 right = middle - 1; n -= 1; } } // 查找失败,即 left > right,返回 -1 return -1; } } 【输出结果:】 查找成功,当前下标为: 1
五、哈希表、树
1、哈希表(散列表)
(1)什么是哈希表?
哈希表是一种 根据 关键码(key) 直接访问值(value)的 一种数据映射结构。其通过一个映射函数,将 关键码 映射到 表中的某一个位置 进行访问(可以提高查找速度)。
哈希表可以使用 数组 + 链表、 或者 数组 + 二叉树 的形式实现。
适用于 查询性能要求高、数据之间无逻辑关系 的场景。
【数组 + 链表 形式实现哈希表:】 基本结构: 使用 数组(连续的存储空间) 表示一个散列表。 每个数组元素 存储的 是一个 单链表(用于存储 映射函数 相同的值)。 即 链表数组,定义一个 链表结构,在用其 定义数组。 基本过程: 对于一个数,通过 散列函数(hash(),可以通过 取模 或者 位运算) 计算 key,并将其映射到 散列表(数组)的 某个位置。 对于相同的 hash 值(产生 hash 冲突),通常采用 拉链法来解决。 简单地讲,就是将 hash(key) 得到的结果 作为 数组的下标,若多个 key 的 hash(key) 相同,那么在当前数组下标的位置建立一个链表来保存数据。 【数组 + 链表 形式实现哈希表 核心代码结构:】 Step1:定义链表节点: /** * 链表节点 * @param <K> key * @param <V> value */ class Node<K, V> { K key; // key,用于 散列函数 计算的值 V value; // value,节点真实存储数据 Node<K, V> next; // 指向下一个节点 public Node(K key, V value) { this.key = key; this.value = value; } } Step2:构建链表: /** * 链表,用于存储数据 * @param <K> * @param <V> */ class NodeList<K, V> { Node<K, V> first; // 第一个节点,即存储真实数据,非头指针 } Step3:构建链表数组,以及散列函数。 /** * 定义 哈希 结构,链表数组 * @param <K> * @param <V> */ class HashTable<K, V> { private int size = 16; // 默认大小为 16 NodeList<K, V>[] table; // 链表数组,散列函数 确定 数组下标位置,数组元素(链表) 用于存储值 public HashTable() { this(16); } public HashTable(int size) { // 保存哈希表大小 this.size = size; // 构建哈希表(数组) this.table = new NodeList[this.size]; // 初始化每个数组元素 -- 链表,否则默认为 null for (int i = 0; i < this.size; i++) { this.table[i] = new NodeList<>(); } } /** * 散列函数,此处以 模运算 为例,可以使用 位运算 * @param key 待计算的 key * @return 哈希值(数组下标) */ public int hash(K key) { return key.hashCode() % size; } } 【实现简单的增、查:】 添加节点: 首先根据 key 通过 散列函数 计算后,得到 数组下标。 根据数组下标定位到 相应的链表,然后进行添加操作。 若当前链表为空,则添加数据为第一个节点。 若当前链表不空,则遍历链表,若发现相同 key,则替换其 value。 若没有相同 key,则遍历到链表末尾并添加节点。 查找节点: 同样根据 key 计算出数组下标,然后定位到相应的链表。 遍历链表,并比较 key,若 key 相同则返回 value, 若链表遍历完成仍不存在相同 key 则返回 null。

(2)代码实现
【代码实现:】 package com.lyh.tree; public class HashTableDemo { public static void main(String[] args) { HashTable<Integer, String> hashTable = new HashTable<>(4); hashTable.list(); System.out.println("================="); for (int i = 0; i < 10; i++) { hashTable.put(i, i + ""); } hashTable.list(); System.out.println("================="); hashTable.put(1, "Java"); hashTable.put(2, "Python"); hashTable.list(); System.out.println("================="); System.out.println("key = 2 的 value 为: " + hashTable.get(2)); } } /** * 定义 哈希 结构,链表数组 * @param <K> * @param <V> */ class HashTable<K, V> { private int size = 16; // 默认大小为 16 NodeList<K, V>[] table; // 链表数组,散列函数 确定 数组下标位置,数组元素(链表) 用于存储值 public HashTable() { this(16); } public HashTable(int size) { // 保存哈希表大小 this.size = size; // 构建哈希表(数组) this.table = new NodeList[this.size]; // 初始化每个数组元素 -- 链表,否则默认为 null for (int i = 0; i < this.size; i++) { this.table[i] = new NodeList<>(); } } /** * 散列函数,此处以 模运算 为例,可以使用 位运算 * @param key 待计算的 key * @return 哈希值(数组下标) */ public int hash(K key) { return key.hashCode() % size; } /** * 向哈希表中添加数据 * @param key * @param value */ public void put(K key, V value) { // 通过 散列函数 根据 key 计算出 数组下标位置,然后向链表中添加数据 this.table[hash(key)].add(key, value); } /** * 查找节点 * @param key 查找条件 * @return 节点数据 */ public V get(K key) { // 通过 散列函数 根据 key 计算出 数组下标位置,然后从链表中取出数据 return this.table[hash(key)].find(key); } /** * 输出哈希表 */ public void list() { // 遍历数组,输出每个链表 for (int i = 0; i < this.size; i++) { this.table[i].list(i); } } } /** * 链表,用于存储数据 * @param <K> * @param <V> */ class NodeList<K, V> { Node<K, V> first; // 第一个节点,即存储真实数据,非头指针 /** * 在链表末尾添加节点 * @param key key * @param value value */ public void add(K key, V value) { // 保存数据到 链表第一个节点 if (first == null) { first = new Node<>(key, value); return; } Node<K, V> temp = first; // 使用临时变量保存 第一个节点,用于辅助链表遍历 // 遍历链表到末尾,并添加节点 while(temp.next != null) { // 如果 key 相等,则替换原来的 value if (key.equals(temp.key)) { temp.value = value; return; } temp = temp.next; } temp.next = new Node<>(key, value); } /** * 遍历输出链表 * @param i 当前数组下标,表示当前为第 i+1 链表 */ public void list(int i) { Node<K, V> temp = first; // 使用临时变量保存 第一个节点,用于辅助链表遍历 // 判断链表是否为空 if (temp == null) { System.out.println("第 " + (i + 1) + " 链表为空"); return; } // 遍历输出链表 System.out.print("第 " + (i + 1) + " 链表为: "); while(temp != null) { System.out.print("[ key = " + temp.key + ", value = " + temp.value + " ] ==> "); temp = temp.next; } System.out.println(); } /** * 查找节点 * @param key 查找条件 * @return 查找失败返回 null,查找成功返回相应节点的 value */ public V find(K key) { Node<K, V> temp = first; // 使用临时变量保存 第一个节点,用于辅助链表遍历 // 遍历链表,若发现相同 key,则返回 while(temp != null) { if (key.equals(temp.key)) { return temp.value; } temp = temp.next; } return null; } } /** * 链表节点 * @param <K> key * @param <V> value */ class Node<K, V> { K key; // key,用于 散列函数 计算的值 V value; // value,节点真实存储数据 Node<K, V> next; // 指向下一个节点 public Node(K key, V value) { this.key = key; this.value = value; } } 【输出结果:】 第 1 链表为空 第 2 链表为空 第 3 链表为空 第 4 链表为空 ================= 第 1 链表为: [ key = 0, value = 0 ] ==> [ key = 4, value = 4 ] ==> [ key = 8, value = 8 ] ==> 第 2 链表为: [ key = 1, value = 1 ] ==> [ key = 5, value = 5 ] ==> [ key = 9, value = 9 ] ==> 第 3 链表为: [ key = 2, value = 2 ] ==> [ key = 6, value = 6 ] ==> 第 4 链表为: [ key = 3, value = 3 ] ==> [ key = 7, value = 7 ] ==> ================= 第 1 链表为: [ key = 0, value = 0 ] ==> [ key = 4, value = 4 ] ==> [ key = 8, value = 8 ] ==> 第 2 链表为: [ key = 1, value = Java ] ==> [ key = 5, value = 5 ] ==> [ key = 9, value = 9 ] ==> 第 3 链表为: [ key = 2, value = Python ] ==> [ key = 6, value = 6 ] ==> 第 4 链表为: [ key = 3, value = 3 ] ==> [ key = 7, value = 7 ] ==> ================= key = 2 的 value 为: Python
2、树
(1)什么是树?
树是一种 由 n 个节点组成的一种 具有层次关系的、类似树形的 数据结构。
其每个节点 均有 零个或 多个 子节点,每一个节点最多只有一个 父节点,没有父节点的 节点 称为 根节点。
(2)为什么需要树 这种 数据结构?
前面介绍了 数组、链表、以及 哈希表 等数据结构,可以用来存储数据。
所谓 存在即合理,每种数据结构的出现,必然能解决某种问题,下面分析一下优缺点。
【数组存储:】 数组采用 连续的 存储方式来 存储元素。查询快、增删慢。 优点: 可以通过 下标的方式 来访问(查找)元素,速度快。 且对于有序数组,可以通过 折半查找、插值查找 等方式提高 查找(检索)效率。 缺点: 对于 插入操作,可能会伴随着 数组扩容、数组元素整体后移等操作,效率较低。 【链表存储:】 链表采用 不连续的 存储方式来 存储元素。增删快、查询慢。 优点: 插入、删除节点时,无需整体移动元素,只需要修改 前、后 指针域 即可。效率较高。 缺点: 进行查找时,需要从头开始遍历链表,若链表过长,查询效率将会较低。 【哈希存储:】 哈希 采用 数组 + 链表 的方式存储元素,每个 数组元素 存储的是一个 链表。 优点: 其结合了 数组、链表 的优点,增、删、改、查 效率都可以,时间复杂度为 O(1)。 缺点: 由于哈希 存储的元素是无序的,若想按 顺序输出,实现起来就有点 麻烦。 且哈希只是单次查询效率高,若执行 n 次查找,时间复杂度将退化到 O(n)。 哈希表由数组实现,扩容也是影响效率的一个问题。 【树存储:(以二叉排序树为例)】 二叉排序树要求 任何一个 非叶子节点,其左子节点小于 当前节点,其右子节点 大于当前节点。 即 数据是有序的(中序遍历可得到有序序列)。其在一定程度上保证 增删 以及 查找的速率 较高。 注: 二叉排序树可能存在三种定义: 左子节点 小于等于 当前节点,右子节点 大于 当前节点。 左子节点 小于 当前节点,右子节点 大于等于 当前节点。 左子节点 小于 当前节点,右子节点 大于 当前节点。
(3)常见树分类:
二叉树、二叉排序树(BST)、平衡二叉树(AVL)、2-3 树、B 树(B-Tree)、B+ 树、赫夫曼树、红黑树 等。
3、二叉树、遍历二叉树(递归实现 前序、中序、后序 遍历)
(1)二叉树基本概念:
二叉树 是一种要求 每个节点 最多只有 两个子节点 的树结构。
注:
树 转 数组:
可以通过 前序遍历、中序遍历、后序遍历 三种遍历形式 遍历 二叉树 得到。
数组 转 树:
根据 前序遍历 + 中序遍历 得到的数组数据 逆向推出 二叉树。
根据 中序遍历 + 后序遍历 得到的数组数据 逆向推出 二叉树。
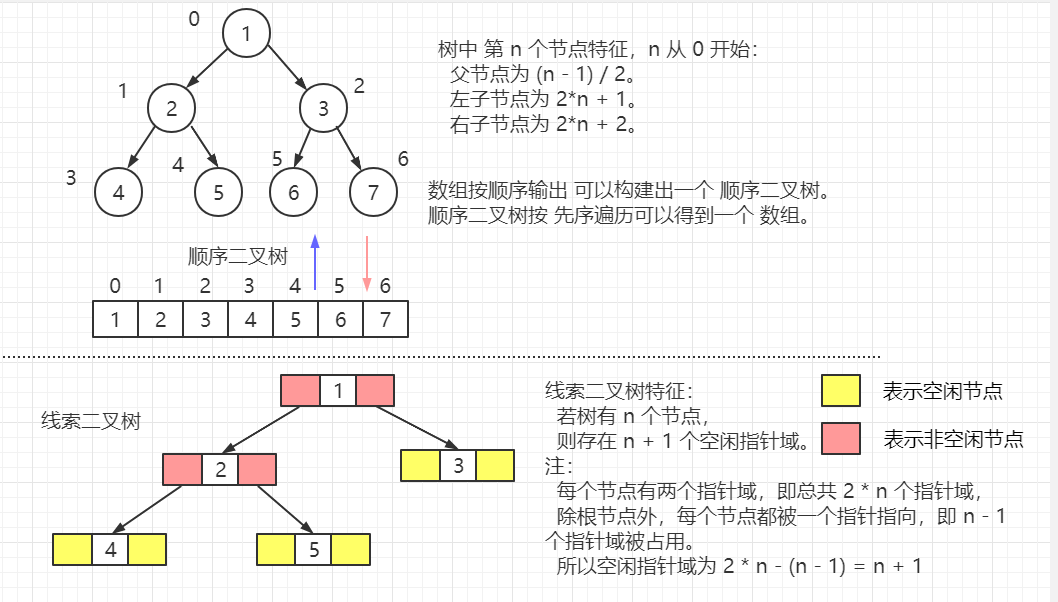
根据顺序二叉树的 特点(2*n + 1 、2*n + 2) 构建 顺序二叉树。
【二叉树常见分类:】 满二叉树: 如果 一个 n 层的二叉树 的所有叶子节点均在最后一层, 且节点总数为 2^n - 1,则该树为 满二叉树。 完全二叉树: 一棵深度为 k 的有 n 个结点的二叉树,对树中的结点按从上至下、从左到右的顺序进行编号, 如果编号为 i(1 ≤ i ≤ n)的结点与满二叉树中编号为 i 的结点在二叉树中的位置相同,则这棵二叉树称为完全二叉树。 顺序二叉树: 是二叉树的一种 存储形式(按照数组顺序,从上到下、从左到右 依次 给二叉树 添加树节点,得到一个完全二叉树 或者 满二叉树), 其 可以在 数组 与 树 之间相互转换。即 根据一个数组,可以得到 树 的结构,从树也可以反推 数组。 特点: 顺序二叉树通常只考虑 完全二叉树。 其第 n 个元素的左子节点为 2*n + 1。 其第 n 个元素的右子节点为 2*n + 2。 其第 n 个元素的父节点为 (n - 1) / 2。 (n 从 0 开始,即从数组第一个元素下标开始计数)。 线索二叉树: 对于 n 个节点的 二叉树,其总共含有 2*n - (n - 1) = n + 1 个空的指针域。 利用这些空的指针域,存放 当前节点 在 某次遍历(前序、中序、后续)下的 前驱、后继 节点的指针。 这些指向 前驱、后继 节点的指针称为 线索,使用这种线索的二叉树 称为线索二叉树。 即 线索二叉树的本质 是 将二叉树 当前节点的空闲指针 改为 指向当前节点 前驱 或者 后继 节点的过程。 而根据遍历的分类,前驱、后继节点会不同,可以分为: 前序线索二叉树、中序线索二叉树、后序线索二叉树。 还有 二叉搜索树(BST)、平衡二叉搜索树(AVT)等后续介绍。

(2)二叉树三种遍历方式(树 转 数组)
树 转 数组:
树 转 数组,也即 树的各节点 的遍历顺序,按照 当前节点、左子节点、右子节点 遍历的先后可以分为三种遍历:前序遍历、中序遍历、后序遍历。
此时以 递归方式实现,后续会补充 迭代实现。
【前序遍历:】 节点遍历顺序: 先输出 当前节点,再输出 左子节点,最后输出 右子节点。 遍历、查找步骤: 对于一颗 二叉树,若二叉树为空,则直接结束。 否则 输出 当前节点(若为查找,则在此处进行 值 比较,查找成功则退出)。 前序遍历 左子树。 前序遍历 右子树。 删除节点: 删除的规则可以自定义,不同的规则对应不同的代码实现。 比如:删除某带有左、右子树的节点,是整体删除 还是 将子节点 旋转到当前节点位置。 此处以整体删除为例: 由于二叉树是单向的(此处可以理解成 单链表 删除处理), 需要判断 当前节点的 子节点 是否为待删除的节点。若是,则直接将当前节点 子节点 置 null 即可。 即: if (this.left.data == key) { this.left = null; return; } if (this.right.data == key) { this.right = null; return; } 【中序遍历:】 节点遍历顺序: 先输出 左子节点,再输出 当前节点,最后输出 右子节点。 遍历、查找步骤: 对于一颗 二叉树,若二叉树为空,则直接结束。 否则 前序遍历 左子树。 输出 当前节点(若为查找,则在此处进行 值 比较)。 前序遍历 右子树。 【后序遍历:】 节点遍历顺序: 先输出 左子节点,再输出 右子节点,最后输出 当前节点。 遍历、查找步骤: 对于一颗 二叉树,若二叉树为空,则直接结束。 否则 前序遍历 左子树。 前序遍历 右子树。 输出 当前节点(若为查找,则在此处进行 值 比较)。 【代码实现:】 package com.lyh.tree; /** * 构建二叉树 * @param <K> */ public class BinaryTree<K> { private TreeNode<K> root; // 设置根节点 public BinaryTree(TreeNode<K> root) { this.root = root; } public static void main(String[] args) { // 构建二叉树 TreeNode<String> root = new TreeNode<>("0"); TreeNode<String> treeNode = new TreeNode<>("1"); TreeNode<String> treeNode2 = new TreeNode<>("2"); TreeNode<String> treeNode3 = new TreeNode<>("3"); TreeNode<String> treeNode4 = new TreeNode<>("4"); root.left = treeNode; root.right = treeNode2; treeNode.left = treeNode3; treeNode.right = treeNode4; // 设置树 根节点 BinaryTree<String> binaryTree = new BinaryTree<>(root); // 前序遍历 System.out.print("前序遍历: "); binaryTree.prefixList(); System.out.println("\n====================="); // 中序遍历 System.out.print("中序遍历: "); binaryTree.infixList(); System.out.println("\n====================="); // 后序遍历 System.out.print("后序遍历: "); binaryTree.suffixList(); System.out.println("\n====================="); // 前序查找 System.out.print("前序查找, "); TreeNode<String> search = binaryTree.prefixSearch("1"); if (search != null) { System.out.println("查找成功, 当前节点为: " + search + " ,其左节点为: " + search.left + " ,其右节点为: " + search.right); } else { System.out.println("查找失败"); } System.out.println("\n====================="); // 删除节点 System.out.print("删除节点, "); int result = binaryTree.deleteNode("3"); if (result != -1) { System.out.println("成功"); } else { System.out.println("失败"); } System.out.print("当前树的前序遍历为: "); binaryTree.prefixList(); System.out.println("\n====================="); } /** * 前序遍历 */ public void prefixList() { // 判断根节点是否存在 if (root == null) { System.out.println("当前树为 空树"); return; } // 存在根节点,则进行前序遍历 root.prefixList(); } /** * 前序查找 */ public TreeNode<K> prefixSearch(K data) { // 判断根节点是否存在 if (root == null) { return null; } // 存在根节点,则进行前序遍历 return root.prefixSearch(data); } /** * 中序遍历 */ public void infixList() { // 判断根节点是否存在 if (root == null) { System.out.println("当前树为 空树"); return; } // 存在根节点,则进行中序遍历 root.infixList(); } /** * 后序遍历 */ public void suffixList() { // 判断根节点是否存在 if (root == null) { System.out.println("当前树为 空树"); return; } // 存在根节点,则进行后序遍历 root.suffixList(); } /** * 删除节点,删除失败返回 -1,否则返回 1 * @param data 待删除节点 * @return 删除失败返回 -1,否则返回 1 */ public int deleteNode(K data) { // 当根节点存在时,才可以进行删除节点操作 if (root != null) { // 若恰好为 根节点,则直接将根节点置 null if (data.equals(root.data)) { root = null; return 1; } // 否则递归删除 return root.deleteNode(data); } return -1; } } /** * 定义树节点 * @param <K> */ class TreeNode<K> { K data; // 保存节点数据 TreeNode<K> left; // 保存节点的 左子节点 TreeNode<K> right; // 保存节点的 右子节点 public TreeNode(K data) { this.data = data; } @Override public String toString() { return "TreeNode{ data= " + data + "}"; } /** * 前序遍历 */ public void prefixList() { // 输出当前节点 System.out.print(this + " "); // 若左子树不为空,则递归前序遍历 左子树 if (this.left != null) { this.left.prefixList(); } // 若右子树不为空,则递归前序遍历 右子树 if (this.right != null) { this.right.prefixList(); } } /** * 前序查找 * @param data 待查找数据 * @return 查找失败返回 null,查找成功返回相应的数据 */ public TreeNode<K> prefixSearch(K data) { // 若当前节点即为待查找节点,则直接返回 if (data.equals(this.data)) { return this; } TreeNode<K> result = null; // 用于保存查找节点 // 如果左子树不为空,则递归前序查找 左子树 if (this.left != null) { result = this.left.prefixSearch(data); } // 若左子树查找成功,则返回 if (result != null) { return result; } // 如果右子树不为空,则递归前序查找 右子树 if (this.right != null) { result = this.right.prefixSearch(data); } return result; } /** * 中序遍历 */ public void infixList() { // 若左子树不为空,则递归中序遍历 左子树 if (this.left != null) { this.left.infixList(); } // 输出当前节点 System.out.print(this + " "); // 若右子树不为空,则递归中序遍历 右子树 if (this.right != null) { this.right.infixList(); } } /** * 后序遍历 */ public void suffixList() { // 若左子树不为空,则递归后序遍历 左子树 if (this.left != null) { this.left.suffixList(); } // 若右子树不为空,则递归后序遍历 右子树 if (this.right != null) { this.right.suffixList(); } // 输出当前节点 System.out.print(this + " "); } /** * 删除节点,此处若为非叶子节点,直接连同其 子节点 一起删除 * @param data 待删除数据 * @return 删除失败返回 -1,否则 返回 1 */ public int deleteNode(K data) { // 如果删除节点 恰好为 左子节点,则直接将 左子节点 置 null if (this.left != null && data.equals(this.left.data)) { this.left = null; return 1; } // 如果删除节点 恰好为 右子节点,则直接将 右子节点 置 null if (this.right != null && data.equals(this.right.data)) { this.right = null; return 1; } int result = -1; // 若左子树不为 null,则递归左子树 查找节点并删除 if (this.left != null) { result = this.left.deleteNode(data); if (result != -1) { return result; } } // 若右子树不为 null,则递归右子树 查找节点并删除 if (this.right != null) { result = this.right.deleteNode(data); } return result; } } 【输出结果:】 前序遍历: TreeNode{ data= 0} TreeNode{ data= 1} TreeNode{ data= 3} TreeNode{ data= 4} TreeNode{ data= 2} ===================== 中序遍历: TreeNode{ data= 3} TreeNode{ data= 1} TreeNode{ data= 4} TreeNode{ data= 0} TreeNode{ data= 2} ===================== 后序遍历: TreeNode{ data= 3} TreeNode{ data= 4} TreeNode{ data= 1} TreeNode{ data= 2} TreeNode{ data= 0} ===================== 前序查找, 查找成功, 当前节点为: TreeNode{ data= 1} ,其左节点为: TreeNode{ data= 3} ,其右节点为: TreeNode{ data= 4} ===================== 删除节点, 成功 当前树的前序遍历为: TreeNode{ data= 0} TreeNode{ data= 1} TreeNode{ data= 4} TreeNode{ data= 2} =====================
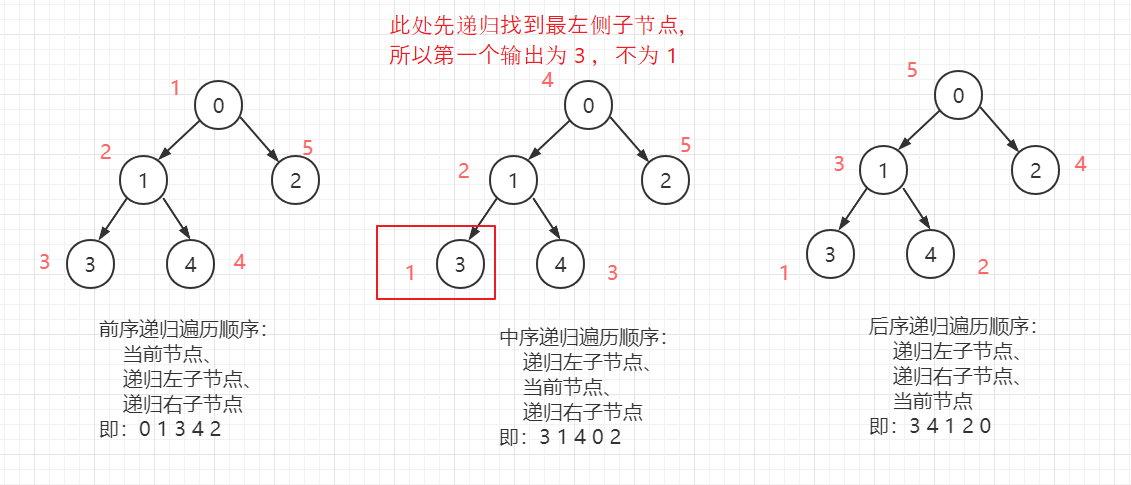
4、还原二叉树(前序 + 中序、后序 + 中序)
(1) 还原二叉树(数组 转 树)
前面通过 前序、中序、后序 遍历 可以 得到树的节点数据,那么根据 前序遍历、中序遍历、后序遍历 得到的数据能否反推 出 树结构呢?
数组 转 树(此处 不考虑 数组中存在相同值的情况,即各个树节点均不同):
使用 前序遍历 + 中序遍历 或者 后序遍历 + 中序遍历 的形式可以反推。
其中:
前序遍历、后序遍历 存在是为了 定位 根节点 所在位置。
根节点定位后,就可以将 中序遍历 数组 分为 左、右 两部分(形成左、右 子树),递归处理即可。
使用 前序 + 后序 数组的方式 虽然可以定位 根节点,但是不知道如何 划分 左、右子树,从而无法正确推导出 二叉树。
(2)思路分析、代码实现
【前序遍历结果 + 中序遍历结果 还原 二叉树:】 前序遍历结果格式为: [{根节点}{左子树}{右子树}] 中序遍历结果格式为: [{左子树}{根节点}{右子树}] 还原步骤: 前序结果 第一个值 必为 根节点(当前节点), 通过该节点,可以将 中序结果 划分为 左子树、右子树。 通过 中序结果 划分的左子树的大小 可以将 前序结果 除根节点外 的值 划分为 左子树、右子树。 然后将 前序、中序 划分的 左子树、右子树 进行递归处理。 举例: 前序遍历结果: [0, 1, 3, 4, 2] 中序遍历结果: [3, 1, 4, 0, 2] 第一次划分: 前序结果:[0, 1, 3, 4, 2],中序结果:[3, 1, 4, 0, 2] 根节点为 0,将中序结果划分为 左子树:[3, 1, 4], 右子树: [2] 根据中序结果 左子树大小划分 前序结果为 左子树:[1, 3 ,4], 右子树:[2] 第二次划分: 前序结果:[1, 3, 4],中序结果:[3, 1, 4] 根节点为 1,将中序结果划分为 左子树:[3], 右子树: [4] 根据中序结果 左子树大小划分 前序结果为 左子树:[3], 右子树:[4] 第三次划分: 前序结果:[3],中序结果:[3] 根节点为 3,将中序结果划分为 左子树:[], 右子树: [] 根据中序结果 左子树大小划分 前序结果为 左子树:[], 右子树:[] 第四次划分: 前序结果、中序结果 均为空,退出。 同理依次进行处理。。。 【后序遍历结果 + 中序遍历结果 还原 二叉树:】 后序遍历结果格式为: [{左子树}{右子树}{根节点}] 中序遍历结果格式为: [{左子树}{根节点}{右子树}] 与 前序遍历 处理类似,只是此时根节点 位于末尾。 还原步骤: 后序结果 最后一个值 必为 根节点(当前节点), 通过该节点,可以将 中序结果 划分为 左子树、右子树。 通过 中序结果 划分的左子树的大小 可以将 后序结果 除根节点外 的值 划分为 左子树、右子树。 然后将 后序、中序 划分的 左子树、右子树 进行递归处理。 【代码实现:】 package com.lyh.tree; import java.util.ArrayList; import java.util.Arrays; import java.util.List; public class ArrayToBinaryTree<K> { public static void main(String[] args) { // 构建二叉树 TreeNode6<String> root = new TreeNode6<>("0"); TreeNode6<String> treeNode = new TreeNode6<>("1"); TreeNode6<String> treeNode2 = new TreeNode6<>("2"); TreeNode6<String> treeNode3 = new TreeNode6<>("3"); TreeNode6<String> treeNode4 = new TreeNode6<>("4"); root.left = treeNode; root.right = treeNode2; treeNode.left = treeNode3; treeNode.right = treeNode4; // 设置树 根节点 ArrayToBinaryTree<String> binaryTree = new ArrayToBinaryTree<>(); // 获取前序遍历结果 List<String> prefixResult = binaryTree.prefixList(root); List<String> prefixResult2 = binaryTree.prefixList2(root); System.out.println("前序遍历结果(方式一): " + prefixResult); System.out.println("前序遍历结果(方式二): " + prefixResult2); System.out.println("================================="); // 获取中序遍历结果 List<String> infixResult = binaryTree.infixList(root); System.out.println("中序遍历结果: " + infixResult); System.out.println("================================="); // 获取后序遍历结果 List<String> suffixResult = binaryTree.suffixList(root); System.out.println("后序遍历结果: " + suffixResult); System.out.println("================================="); // 使用 前序遍历结果 + 中序遍历结果 还原 二叉树 TreeNode6 root2 = binaryTree.prefixAndInfixToTree(prefixResult.toArray(new String[]{}), infixResult.toArray(new String[]{})); System.out.println("还原后的二叉树前序遍历如下: " + binaryTree.prefixList(root2)); System.out.println("还原后的二叉树中序遍历如下: " + binaryTree.infixList(root2)); System.out.println("还原后的二叉树后序遍历如下: " + binaryTree.suffixList(root2)); System.out.println("================================="); // 使用 后序遍历结果 + 中序遍历结果 还原 二叉树 TreeNode6 root3 = binaryTree.suffixAndInfixToTree(suffixResult.toArray(new String[]{}), infixResult.toArray(new String[]{})); System.out.println("还原后的二叉树前序遍历如下: " + binaryTree.prefixList(root3)); System.out.println("还原后的二叉树中序遍历如下: " + binaryTree.infixList(root3)); System.out.println("还原后的二叉树后序遍历如下: " + binaryTree.suffixList(root3)); System.out.println("================================="); } /** * 根据 前序遍历结果 + 中序遍历结果 还原 二叉树(此处不考虑 二叉树 节点相同值,即默认 二叉树 节点均不相同、没有重复元素) * @param prefixResult 前序遍历结果 * @param infixResult 中序遍历结果 * @return 树的根节点 */ public TreeNode6<K> prefixAndInfixToTree(K[] prefixResult, K[] infixResult) { // 递归结束条件 if (prefixResult == null || infixResult == null || prefixResult.length <= 0 || infixResult.length <= 0) { return null; } // 前序遍历结果 第一个值 肯定为 树的根节点 TreeNode6<K> root = new TreeNode6<>(prefixResult[0]); // 查找、记录 中序序列 中 根节点 位置 int index = 0; for (int i = 0; i < infixResult.length; i++) { if (prefixResult[0].equals(infixResult[i])) { index = i; break; } } // 根据 根节点,将 中序遍历结果 划分为 左子树 以及 右子树,中序结果 左边即为左子树,右边即为 右子树 // 中序遍历结果:[{左子树}{根节点}{右子树}] K[] leftInfixResult = Arrays.copyOfRange(infixResult, 0, index); K[] rightInfixResult = Arrays.copyOfRange(infixResult, index + 1, infixResult.length); // 根据左子树 个数,将剩余 前序遍历 结果划分为 左子树、右子树 // 前序遍历结果为:[{根节点}{左子树}{右子树}] K[] leftPrefixResult = Arrays.copyOfRange(prefixResult, 1, leftInfixResult.length + 1); K[] rightPrefixResult = Arrays.copyOfRange(prefixResult, leftInfixResult.length + 1, prefixResult.length); // 设置 根(当前)节点 左、右子树 root.left = prefixAndInfixToTree(leftPrefixResult, leftInfixResult); root.right = prefixAndInfixToTree(rightPrefixResult, rightInfixResult); return root; } /** * 根据 后序遍历结果 + 前序遍历结果 还原 二叉树 * @param suffixResult 后序遍历结果 * @param infixResult 前序遍历结果 * @return 树的根节点 */ public TreeNode6<K> suffixAndInfixToTree(K[] suffixResult, K[] infixResult) { if (suffixResult == null || infixResult == null || suffixResult.length <= 0 || infixResult.length <= 0) { return null; } // 后序遍历结果 最后一个值 肯定为 根节点(当前节点) TreeNode6<K> root = new TreeNode6<>(suffixResult[suffixResult.length - 1]); // 查找、记录 中序序列 中 根节点 位置 int index = 0; for(int i = 0; i < infixResult.length; i++) { if (root.data.equals(infixResult[i])) { index = i; break; } } // 根据 根节点,将 中序遍历结果 划分为 左子树 以及 右子树,中序结果 左边即为左子树,右边即为 右子树 // 中序遍历结果:[{左子树}{根节点}{右子树}] K[] leftInfixResult = Arrays.copyOfRange(infixResult, 0, index); K[] rightInfixResult = Arrays.copyOfRange(infixResult, index + 1, infixResult.length); // 根据左子树 个数,将剩余 后序遍历 结果划分为 左子树、右子树 // 后序遍历结果为:[{左子树}{右子树}{根节点}] K[] leftSuffixResult = Arrays.copyOfRange(suffixResult, 0, leftInfixResult.length); K[] rightSuffixResult = Arrays.copyOfRange(suffixResult, leftInfixResult.length, suffixResult.length - 1); // 设置 根(当前)节点 左、右子树 root.left = suffixAndInfixToTree(leftSuffixResult, leftInfixResult); root.right = suffixAndInfixToTree(rightSuffixResult, rightInfixResult); return root; } /** * 返回前序遍历结果(方式一) * @param root 树的根节点 * @return 前序遍历结果 */ public List<K> prefixList(TreeNode6<K> root) { if (root == null) { System.out.println("当前为空树"); return null; } return root.prefixList(new ArrayList<>()); } /** * 返回前序遍历结果(方式二) * @param root 树的根节点 * @return 前序遍历结果 */ public List<K> prefixList2(TreeNode6<K> root) { if (root == null) { System.out.println("当前为空树"); return null; } List<K> result = new ArrayList<>(); root.prefixList2(result); return result; } /** * 中序遍历 * @param root 树的根节点 * @return 中序遍历结果 */ public List<K> infixList(TreeNode6<K> root) { if (root == null) { System.out.println("当前为空树"); return null; } List<K> result = new ArrayList<>(); root.infixList(result); return result; } /** * 后序遍历 * @param root 树的根节点 * @return 后序遍历结果 */ public List<K> suffixList(TreeNode6<K> root) { if (root == null) { System.out.println("当前为空树"); return null; } List<K> result = new ArrayList<>(); root.suffixList(result); return result; } } /** * 定义树节点 * @param <K> */ class TreeNode6<K> { K data; // 保存节点数据 TreeNode6<K> left; // 保存 左子节点 TreeNode6<K> right; // 保存 右子节点 public TreeNode6(K data) { this.data = data; } /** * 前序遍历(第一种方式:带有返回值的遍历) * @param list 前序遍历序列 * @return 前序遍历结果 */ public List<K> prefixList(List<K> list) { // 用于保存当前序列,作用域只存在当前方法,返回时 作用域消失,即 递归时无需考虑会影响 上一次结果 List<K> result = new ArrayList<>(list); // 添加当前节点 result.add(this.data); // 递归添加左子节点 if (this.left != null) { result = this.left.prefixList(result); } // 递归添加右子节点 if (this.right != null) { result = this.right.prefixList(result); } return result; } /** * 前序遍历(第二种方式:无返回值的遍历) * @param result 前序遍历序列 */ public void prefixList2(List<K> result) { // 保存当前节点 result.add(this.data); // 递归添加左子节点 if (this.left != null) { this.left.prefixList2(result); } // 递归添加右子节点 if (this.right != null) { this.right.prefixList2(result); } } /** * 中序遍历 * @param result 中序遍历序列 */ public void infixList(List<K> result) { // 递归遍历 左子节点 if (this.left != null) { this.left.infixList(result); } // 保存当前节点 result.add(this.data); // 递归遍历 右子节点 if (this.right != null) { this.right.infixList(result); } } /** * 后序遍历 * @param result 后序遍历序列 */ public void suffixList(List<K> result) { // 递归遍历 左子节点 if (this.left != null) { this.left.suffixList(result); } // 递归遍历 右子节点 if (this.right != null) { this.right.suffixList(result); } // 保存当前节点 result.add(this.data); } } 【输出结果:】 前序遍历结果(方式一): [0, 1, 3, 4, 2] 前序遍历结果(方式二): [0, 1, 3, 4, 2] ================================= 中序遍历结果: [3, 1, 4, 0, 2] ================================= 后序遍历结果: [3, 4, 1, 2, 0] ================================= 还原后的二叉树前序遍历如下: [0, 1, 3, 4, 2] 还原后的二叉树中序遍历如下: [3, 1, 4, 0, 2] 还原后的二叉树后序遍历如下: [3, 4, 1, 2, 0] ================================= 还原后的二叉树前序遍历如下: [0, 1, 3, 4, 2] 还原后的二叉树中序遍历如下: [3, 1, 4, 0, 2] 还原后的二叉树后序遍历如下: [3, 4, 1, 2, 0] =================================
5、顺序二叉树(数组 与 树 互转)
(1)什么是顺序二叉树:
是二叉树的一种 存储形式(按照数组顺序,从上到下、从左到右 依次 给二叉树 添加树节点,得到一个完全二叉树 或者 满二叉树),
其 可以在 数组 与 树 之间相互转换。即 根据一个数组,可以得到 树 的结构,从树也可以反推 数组。
特点:
顺序二叉树通常只考虑 完全二叉树。
其第 n 个元素的左子节点为 2*n + 1。
其第 n 个元素的右子节点为 2*n + 2。
其第 n 个元素的父节点为 (n - 1) / 2。 (n 从 0 开始,即从数组第一个元素下标开始计数)。
(2)代码实现:
【核心:】 对于第 n 个元素(n 从 0 开始计数): 其左子节点为 2*n + 1。 其右子节点为 2*n + 2。 无论 数组 转 树 还是 树 转 数组,都是根据这两个 值进行对应。 注: 通过先序、中序、后序 可以遍历树, 那么在遍历的同时将节点 设置到相应的 数组下标处,那么即可完成 树 转 数组。 【代码实现:】 package com.lyh.tree; import java.util.Arrays; public class ArrayBinaryTree<K> { private K[] arrays; public ArrayBinaryTree(K[] arrays) { this.arrays = arrays; } public static void main(String[] args) { // 构建数组 Integer[] arrays = new Integer[]{1, 2, 3, 4, 5, 6, 7}; ArrayBinaryTree<Integer> arrayBinaryTree = new ArrayBinaryTree<>(arrays); // 数组转为 树 TreeNode2 root = arrayBinaryTree.arraysToTree(); // 输出数组 System.out.println("数组为: " + Arrays.toString(arrays)); System.out.println("=============================="); // 输出树 的前序遍历结果 System.out.print("树 的前序遍历为: "); root.prefixList(); System.out.println("\n=============================="); // 输出树 的中序遍历结果 System.out.print("树 的中序遍历为: "); root.infixList(); System.out.println("\n=============================="); // 输出树 的后序遍历结果 System.out.print("树 的后序遍历为: "); root.suffixList(); System.out.println("\n=============================="); System.out.print("树 转为数组为: "); Object[] result = arrayBinaryTree.treeToArray(root); System.out.println(Arrays.toString(result)); } /** * 数组 转 树 * @return 树的根节点,若数组为空 则返回 null。 */ public TreeNode2<K> arraysToTree() { // 若数组为空,则不进行 转树 操作 if (arrays == null || arrays.length == 0) { System.out.println("数据为空,无法转为树"); return null; } // 设置根节点 TreeNode2 root = new TreeNode2(arrays[0]); // 根据数组值 构建树 root.arrayToTree(arrays, 0); return root; } public Object[] treeToArray(TreeNode2<K> root) { // 判断树 是否为空树 if (root == null) { System.out.println("数据为空,无法转为数组"); return null; } // 树非空,计算树节点个数 int length = root.size() + 1; // 声明一个数组 Object[] arrays = new Object[length]; // 将树的数据 放入 数组对应 下标处 root.treeToArray(arrays, 0); return arrays; } } /** * 定义树节点 * @param <K> */ class TreeNode2<K> { K data; // 保存节点数据 TreeNode2<K> left; // 保存节点的 左子节点 TreeNode2<K> right; // 保存节点的 右子节点 public TreeNode2(K data) { this.data = data; } @Override public String toString() { return "TreeNode2{ data = " + data + " }"; } /** * 数组 转 树 * @param arrays 待转换数组 * @param index 当前数组下标(从 0 开始,表示数组第一个元素,同样表示为 根节点) */ public void arrayToTree(K[] arrays, int index) { // 若当前节点存在 左节点,则递归构建 左子树 if (index * 2 + 1 < arrays.length) { this.left = new TreeNode2<>(arrays[index * 2 + 1]); this.left.arrayToTree(arrays, index * 2 + 1); } // 若当前节点存在 右节点,则递归构建 右子树 if (index * 2 + 2 < arrays.length) { this.right = new TreeNode2<>(arrays[index * 2 + 2]); this.right.arrayToTree(arrays, index * 2 + 2); } } /** * 二叉树 转 数组(先序遍历实现) * @param arrays 待转换数组 * @param index 数组下标 */ public void treeToArray(Object[] arrays, int index) { // 设置当前节点 到相应的数组下标处 arrays[index] = this.data; // 遍历左子树 if (this.left != null) { this.left.treeToArray(arrays, index * 2 + 1); } // 遍历右子树 if (this.right != null) { this.right.treeToArray(arrays, index * 2 + 2); } } /** * 前序遍历 */ public void prefixList() { // 输出当前节点 System.out.print(this + " "); // 若左子树不为空,则递归前序遍历 左子树 if (this.left != null) { this.left.prefixList(); } // 若右子树不为空,则递归前序遍历 右子树 if (this.right != null) { this.right.prefixList(); } } /** * 中序遍历 */ public void infixList() { // 若左子树不为空,则递归中序遍历 左子树 if (this.left != null) { this.left.infixList(); } // 输出当前节点 System.out.print(this + " "); // 若右子树不为空,则递归中序遍历 右子树 if (this.right != null) { this.right.infixList(); } } /** * 后序遍历 */ public void suffixList() { // 若左子树不为空,则递归后序遍历 左子树 if (this.left != null) { this.left.suffixList(); } // 若右子树不为空,则递归后序遍历 右子树 if (this.right != null) { this.right.suffixList(); } // 输出当前节点 System.out.print(this + " "); } /** * 求树节点总数 * @return 树节点总数 */ public int size() { int left = 0; // 左节点个数 int right = 0; // 右节点个数 // 递归求左节点个数 if (this.left != null) { left = 1 + this.left.size(); } // 递归求右节点个数 if (this.right != null) { right = 1 + this.right.size(); } // 返回总个数 return left + right; } } 【输出结果:】 数组为: [1, 2, 3, 4, 5, 6, 7] ============================== 树 的前序遍历为: TreeNode2{ data = 1 } TreeNode2{ data = 2 } TreeNode2{ data = 4 } TreeNode2{ data = 5 } TreeNode2{ data = 3 } TreeNode2{ data = 6 } TreeNode2{ data = 7 } ============================== 树 的中序遍历为: TreeNode2{ data = 4 } TreeNode2{ data = 2 } TreeNode2{ data = 5 } TreeNode2{ data = 1 } TreeNode2{ data = 6 } TreeNode2{ data = 3 } TreeNode2{ data = 7 } ============================== 树 的后序遍历为: TreeNode2{ data = 4 } TreeNode2{ data = 5 } TreeNode2{ data = 2 } TreeNode2{ data = 6 } TreeNode2{ data = 7 } TreeNode2{ data = 3 } TreeNode2{ data = 1 } ============================== 树 转为数组为: [1, 2, 3, 4, 5, 6, 7]
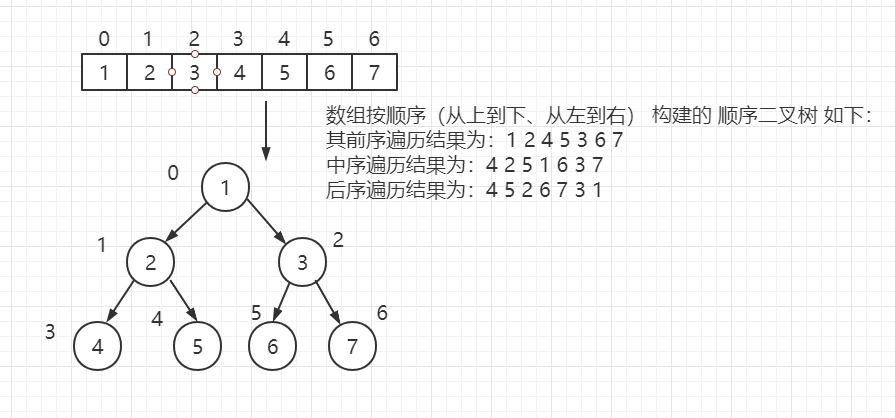
6、线索二叉树
(1)什么是线索二叉树?
对于 n 个节点的 二叉树,其总共含有 2*n - (n - 1) = n + 1 个空的指针域。
利用这些空的指针域,存放 当前节点 在 某次遍历(前序、中序、后续)下的 前驱、后继 节点的指针。
这些指向 前驱、后继 节点的指针称为 线索,使用这种线索的二叉树 称为线索二叉树。
即 线索二叉树的本质 是 将二叉树 当前节点的空闲指针 改为 指向当前节点 前驱 或者 后继 节点的过程。
而根据遍历的分类,前驱、后继节点会不同,可以分为:
前序线索二叉树、中序线索二叉树、后序线索二叉树。
(2)代码实现 中序线索二叉树
【定义树节点:】 对于每个节点的 左、右指针域 来说,可能是 空闲指针域,也可能指向 左、右 子节点。 需要对其进行区分,可以定义指针类型,比如:leftType,值为 0 时表示指向子节点, 值为 1 时表示为 空闲指针域(存储线索 -- 前驱、后继节点) 树节点: class TreeNode3<K> { K data; // 保存节点数据 TreeNode3<K> left; // 保存左子节点 TreeNode3<K> right; // 保存右子节点 byte leftType; // 值为 0 时表示为 左子节点,值为 1 时表示存储线索 -- 前驱节点 byte rightType; // 值为 0 时表示为 右子节点,值为 1 时表示存储线索 -- 后继节点 public TreeNode3(K data) { this.data = data; } @Override public String toString() { return "TreeNode3{ data= " + data + " }"; } } 【构建线索二叉树(以 中序遍历 构建 线索二叉树 为例):】 首先得构建一个 二叉树,可以使用 顺序二叉树(详见上例,数组 转 二叉树) 或者 手动构建。 中序遍历二叉树时,无法直接 明确 当前节点的 前驱、后继 节点。 可以使用变量 preNode 用于记录 当前节点的前驱节点。 若 当前节点 node 的左指针域 left 为 null,则将其 指向 前驱节点 preNode,并修改指针类型为 线索。 若 前驱节点 preNode 的右指针域 right 为 null,则将其 指向 当前节点 node,并修改指针类型为 线索。 在进入下一个 节点前,需要使用 前驱节点 保存 当前节点。 注: 此处使用变量记录 前驱节点 即可,当然使用 另一个变量 nextNode 记录 后继节点亦可实现。 即: // 设置前驱节点 if (node.left == null) { node.left = preNode; // 指向 当前节点 的前驱节点 node.leftType = 1; // 修改左指针域 指针类型为 线索 } // 设置后继节点 if (preNode != null && preNode.right == null) { preNode.right = node; preNode.rightType = 1; // 修改右指针域 指针类型为 线索 } // 进入下一个节点前,保存当前节点,作为前驱节点 preNode = node; 【遍历 线索二叉树(使用中序遍历 并根据 后继节点 的方式输出 中序线索二叉树):】 由于 树节点 的 左、右指针 并不一定为空(存放了 前驱、后继 节点),原始的二叉树 前序、中序、后序遍历 方式已不适用。 但是一般通过其 前驱节点 或者 后继节点 查找。 以后继节点为例: 与 原始遍历 相同,按照 左子节点、当前节点、右子节点 的顺序 访问。 访问左子树,若 当前节点 左子节点为 线索(指向 前驱节点),则输出 当前节点,若不是,则按照 中序遍历 方式进行遍历。 访问右子树,若 当前节点 右子节点为 线索(指向 后继节点),则输出 后继节点,若不是,则按照 中序遍历 方式进行遍历。 即: // 从 根节点 开始遍历(中序方式) while(node != null) { // 遍历左指针域, leftType = 0 时为左子树,依次往下遍历,直至 leftType = 1。表示当前节点的左指针域 线索化(即当前节点为有效节点) while(node.leftType == 0) { node = node.left; } // 操作当前节点 System.out.print(node + " "); // 遍历右指针域,若当前节点的 右指针域 线索化,则输出当前节点的 后继节点 while(node.rightType == 1) { node = node.right; System.out.print(node + " "); } // 当前节点 右指针域 非线索化,则替换当前节点,开始下一次循环 node = node.right; } 前驱节点方式: 与后继节点相反处理,按照 右子节点、当前节点、左子节点 的顺序访问。 最后返回的是 树的 逆序中序遍历 的顺序。 【代码实现:】 package com.lyh.tree; import java.util.Arrays; /** * 线索二叉树 * @param <K> */ public class ThreadBinaryTree<K> { private TreeNode3<K> preNode; // 用于记录当前节点的上一个节点 public static void main(String[] args) { // 将数组 转为 顺序二叉树 Integer[] arrays = new Integer[]{1, 2, 3, 4, 5}; ThreadBinaryTree<Integer> threadBinaryTree = new ThreadBinaryTree<>(); TreeNode3<Integer> root = threadBinaryTree.arrayToTree(arrays, 0); // 使用 中序遍历 遍历 顺序二叉树,并添加线索,使其成为 中序线索二叉树 threadBinaryTree.infixCreateThreadBinaryTree(root); // 中序遍历 以 后继节点 的方式 输出 中序线索二叉树 System.out.println("原数组为: " + Arrays.toString(arrays)); System.out.println("数组 ==> 转为中序线索二叉树(后继节点方式) 输出为: "); threadBinaryTree.infixNextNodeList(root); System.out.println("\n数组 ==> 转为中序线索二叉树(前驱节点方式) 输出为: "); threadBinaryTree.infixPreNodeList(root); } /** * 根据数组构建一个 顺序二叉树 * @param arrays 数组 * @param index 数组下标 * @return 顺序二叉树 */ public TreeNode3<K> arrayToTree(K[] arrays, int index) { TreeNode3<K> root = null; // 设置根节点 // 递归数组并将对应的值存入 顺序二叉树 if (index >= 0 && index < arrays.length) { // 设置当前节点 root = new TreeNode3<>(arrays[index]); // 设置当前节点左子节点 root.left = arrayToTree(arrays, index * 2 + 1); // 设置当前节点右子节点 root.right = arrayToTree(arrays, index * 2 + 2); } return root; } /** * 中序遍历并创建线索化二叉树 * @param node 树节点 */ public void infixCreateThreadBinaryTree(TreeNode3<K> node) { // 判断当前节点是否为空,即 叶子节点 或者 空树 if (node == null) { return; } // 遍历左子节点 infixCreateThreadBinaryTree(node.left); // 操作当前节点 // 设置前驱节点 if (node.left == null) { node.left = preNode; // 指向 当前节点 的前驱节点 node.leftType = 1; // 修改左指针域 指针类型为 线索 } // 设置后继节点 if (preNode != null && preNode.right == null) { preNode.right = node; preNode.rightType = 1; // 修改右指针域 指针类型为 线索 } // 进入下一个节点前,保存当前节点,作为前驱节点 preNode = node; // 遍历右子节点 infixCreateThreadBinaryTree(node.right); } /** * 以中序遍历方式 并根据 后继节点 输出 中序线索二叉树 * @param node 根节点 */ public void infixNextNodeList(TreeNode3<K> node) { // 从 根节点 开始遍历(中序方式) while(node != null) { // 遍历左指针域, leftType = 0 时为左子树,依次往下遍历,直至 leftType = 1。表示当前节点的左指针域 线索化(即当前节点为有效节点) while(node.leftType == 0) { node = node.left; } // 操作当前节点 System.out.print(node + " "); // 遍历右指针域,若当前节点的 右指针域 线索化,则输出当前节点的 后继节点 while(node.rightType == 1) { node = node.right; System.out.print(node + " "); } // 当前节点 右指针域 非线索化,则替换当前节点,开始下一次循环 node = node.right; } } /** * 以中序遍历方式 并根据 前驱节点 反向输出 中序线索二叉树 * @param node 根节点 */ public void infixPreNodeList(TreeNode3 node) { // 从根节点开始遍历 while(node != null) { // 遍历右指针域,找到线索化 节点 while(node.right != null && node.rightType == 0) { node = node.right; } // 操作当前节点 System.out.print(node + " "); // 遍历左指针域,若当前左指针域 线索化,则输出当前节点的 前驱节点 while(node.left != null && node.leftType == 1) { node = node.left; System.out.print(node + " "); } // 当前节点 左指针域 非线索化,则替换当前节点,开始下一次循环 node = node.left; } } } /** * 定义树节点 * @param <K> */ class TreeNode3<K> { K data; // 保存节点数据 TreeNode3<K> left; // 保存左子节点 TreeNode3<K> right; // 保存右子节点 byte leftType; // 值为 0 时表示为 左子节点,值为 1 时表示存储线索 -- 前驱节点 byte rightType; // 值为 0 时表示为 右子节点,值为 1 时表示存储线索 -- 后继节点 public TreeNode3(K data) { this.data = data; } @Override public String toString() { return "TreeNode3{ data= " + data + " }"; } } 【输出结果:】 原数组为: [1, 2, 3, 4, 5] 数组 ==> 转为中序线索二叉树(后继节点方式) 输出为: TreeNode3{ data= 4 } TreeNode3{ data= 2 } TreeNode3{ data= 5 } TreeNode3{ data= 1 } TreeNode3{ data= 3 } 数组 ==> 转为中序线索二叉树(前驱节点方式) 输出为: TreeNode3{ data= 3 } TreeNode3{ data= 1 } TreeNode3{ data= 5 } TreeNode3{ data= 2 } TreeNode3{ data= 4 }
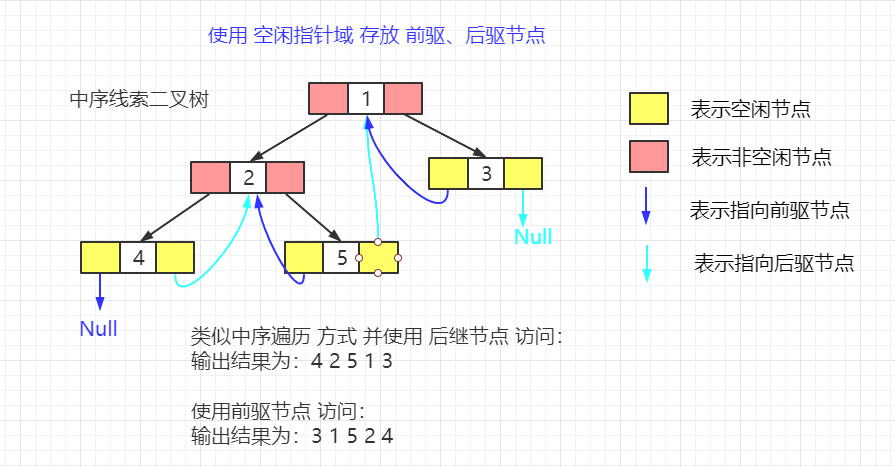
7、哈夫曼树(HuffmanTree、最优二叉树)
(1)什么是哈夫曼树?
哈夫曼树 又称 最优二叉树。对于 n 个节点 且 每个节点有一个值(权值),将这 n 个节点构建成一个 二叉树,使得该树的 带权路径长度(weighted path length,简称 wpl)最小。这样的二叉树 称为 最优二叉树(或者 哈夫曼树)。
注:
哈夫曼树构建完成后,n 个节点 均为 哈夫曼树 的叶子节点。
【基本关键词概念:】
路径 与 路径长度:
在一棵树中,一个节点 到达 另一个节点 之间的 分支通路 称为 路径。
通路中 分支的总数 称为 路径长度。
节点的权:
简单的理解为 节点中带有某含义的值。
节点的带权路径长度:
从根节点 到 该节点之间的路径长度 与 该节点的 权的乘积。
树的带权路径长度:
该树所有的 叶子节点 的带权路径长度 之和。
哈夫曼树(最优二叉树):
树的带权路径(wpl)最小的二叉树 为 哈夫曼树。
一般权值越大的节点 离 根节点 越近 的二叉树才是最优二叉树。
wpl 相同的二叉树 其 哈夫曼树可能不同。
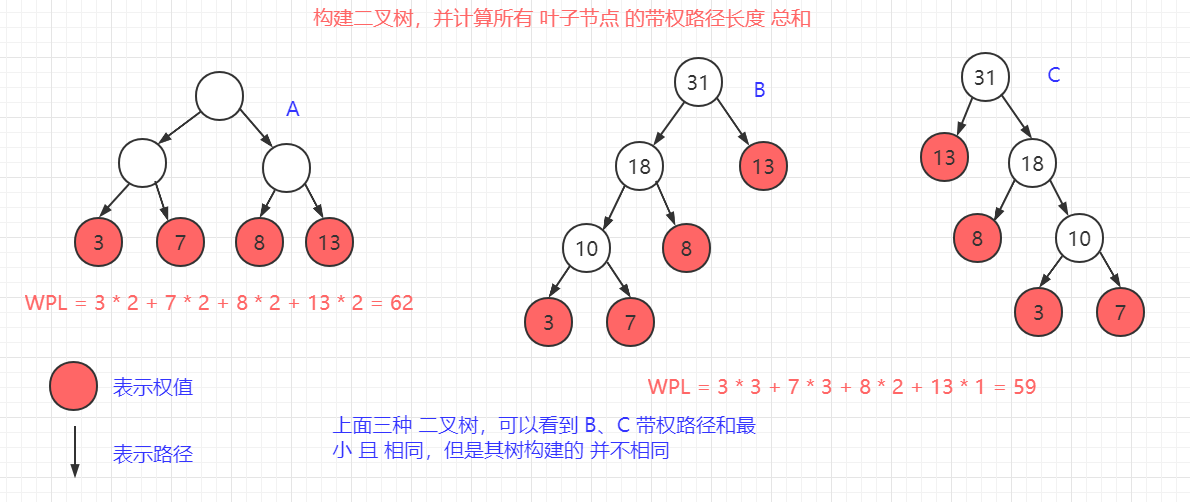
(2)创建 哈夫曼树
【哈夫曼树创建步骤:】 Step1:对于一组数据,先将数据 按照 权值 从小到大 排序。 Step2:将数据中每一个值 视为一个树节点(最简单的二叉树), Step2.1:从数据中选取 权值 最小的两个值 作为 左、右子节点 并构建一个新的二叉树。 Step2.2:新的二叉树 权值为 左、右子节点 权值之和。 Step2.3:删除已被选择的左、右节点,并将新的节点 加入 数据中(按照权值从小到大排序)。 Step3:重复 Step2 操作,直至数据中只剩 一个值,即 哈夫曼树的 根节点。 注: 一般来说 权值最大 的叶子节点 离 根节点越近的 二叉树为 最优二叉树。 所以每次拼接时,均选取当前节点中 最小权值的两个节点进行拼接,将最大权值的节点留在最后拼接。 【代码实现:】 package com.lyh.tree; import java.util.ArrayList; import java.util.Arrays; import java.util.Collections; import java.util.List; /** * 哈夫曼树 */ public class HuffmanTree<K> { public static void main(String[] args) { // 根据数组构建哈夫曼树(此处构建规则为 左子节点权值 小于 右子节点) int[] arrays = new int[]{8, 3, 7, 13}; HuffmanTree<String> huffmanTree = new HuffmanTree<>(); TreeNode4 root = huffmanTree.createHuffmanTree(arrays); // 输出哈夫曼树前序遍历 System.out.print("哈夫曼树前序遍历为: "); root.prefixList(); } /** * 构建哈夫曼树,返回树的根节点 * @param arrays 待构建树的数组(节点 权值 组成的数组) * @return 哈夫曼树根节点 */ public TreeNode4<K> createHuffmanTree(int[] arrays) { // 构建树节点,此处借用 集合,并利用集合进行排序操作 List<TreeNode4<K>> lists = new ArrayList<>(); Arrays.stream(arrays).forEach( x -> { lists.add(new TreeNode4<>(x)); }); // 遍历构建哈夫曼树,此处规则为 左子节点权值 小于 右子节点权值 while (lists.size() > 1) { // 节点按权值 从小到大排序 Collections.sort(lists); // 获取左子节点 TreeNode4<K> leftNode = lists.get(0); // 获取右子节点 TreeNode4<K> rightNode = lists.get(1); // 组合成 二叉树 TreeNode4<K> parentNode = new TreeNode4<>(leftNode.value + rightNode.value); parentNode.left = leftNode; parentNode.right = rightNode; // 从集合中移除已使用节点,并将新节点添加到集合中 lists.remove(leftNode); lists.remove(rightNode); lists.add(parentNode); } // 集合中最后元素即为 哈夫曼树 根节点 return lists.get(0); } } /** * 定义树节点 * @param <K> */ class TreeNode4<K> implements Comparable<TreeNode4<K>>{ K data; // 保存节点值 int value; // 保存节点权值 TreeNode4<K> left; // 保存左子节点 TreeNode4<K> right; // 保存右子节点 public TreeNode4(int value) { this.value = value; } @Override public String toString() { return "TreeNode4{ value = " + value + " }"; } @Override public int compareTo(TreeNode4<K> o) { return this.value - o.value; } /** * 前序遍历 */ public void prefixList() { // 输出当前节点 System.out.print(this + " "); // 遍历左子节点 if (this.left != null) { this.left.prefixList(); } // 遍历右子节点 if (this.right != null) { this.right.prefixList(); } } } 【输出结果:】 哈夫曼树前序遍历为: TreeNode4{ value = 31 } TreeNode4{ value = 13 } TreeNode4{ value = 18 } TreeNode4{ value = 8 } TreeNode4{ value = 10 } TreeNode4{ value = 3 } TreeNode4{ value = 7 }
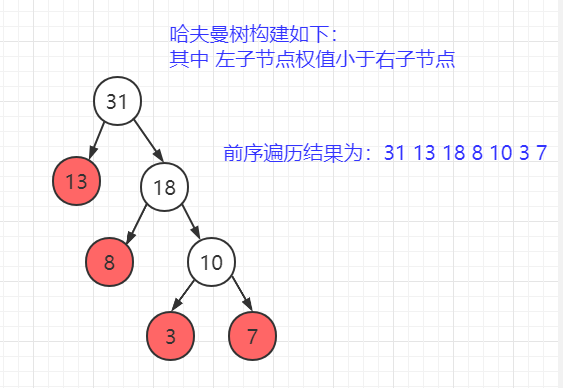
8、哈夫曼编码 实现 文件压缩、解压
(1)什么是 哈夫曼编码?
哈夫曼编码 是一种 可变字长编码,可用于数据压缩、节省存储空间。
将文件转为 字节数组,并根据 各字节 出现频率为权值,构建哈夫曼树,并得到每个字节的 哈夫曼编码(出现频率越高的字节 其编码 越短,从而达到缩减存储空间的目的),再根据 哈夫曼编码将 字节转换为对应的 二进制 串,最后以 8 位为单位 压缩二进制串 成 字节数组,即可实现 文件的压缩。
(2)补充点 二进制 与 整数 相互转换的概念
【Java 中二进制 与 整数 互相转换:】 String 转 int: int parseInt(String s, int radix); 其中: s 表示 二进制字符串, radix 表示进制, 即 按照 几进制 去 处理 二进制字符串。 int 转 String: String toBinaryString(int i); 其中: i 表示待转换的整数。 注: 若结果为非负数,输出结果 前面的 0 会省略(处理时需要额外注意)。 比如: 5 可以为 101、0101、00101,,但是最终输出结果为 101. int 转 byte(强转): byte (byte)parseInt(String s, int radix) 【Java 中整数以 二进制 补码形式存储:】 Java 中整数使用 二进制 补码 的形式存储, 正数的 补码、反码、原码 均相同。 负数的 补码为 反码 加 1。 反码为 符号位不变,其余各位取反。 比如: "10000101" 转为 int 型整数时, 即 Integer.parseInt("10000101", 2); 由于 "1000 0101" 转为 int,而 int 为 4 字节,即为 "0000 0000 0000 0000 0000 0000 1000 0101", 其符号位为 0,即整数,补码与原码相同,即最终显示为整数 133. "10000101" 转为 byte 型整数时,即 (byte)Integer.parseInt("10000101", 2); 由于 "10000101" 转为 byte,而 byte 为 1 字节,即为 "10000101", 其符号位为 1,表示负数,其反码为符号位不变,各位取反,即 "11111010"。 而 补码为其反码 加 1,即最终为 "11111011",即最终显示为整数 -123. 注: byte 范围为 -128 ~ 127,即 10000000 ~ 01111111。符号位不做计算。 【压缩处理最后一个字节可能遇到的问题:】 以 8 位为单位 将 二进制串 转为 字节(整数)数组 的时候,若 最后一个二进制串 不足 8 位,需要额外注意: 若不足 8 位直接存储为 字节,则解码时 可能会出错。 比如: (byte)Integer.parseInt("0101", 2); 转为 byte 时其值为 5. (byte)Integer.parseInt("00101", 2); 转为 byte 时其值也为 5. 若直接存储,那么解码时, Integer.toBinaryString(5); 输出为 101, 由于转换的是非负数,其前面的 0 会省略。并不知道其前面到底有 几个 0,从而解码失败。 我的解决方法是: 额外增加一个字节用于记录 最后一个 二进制串 的实际位数。 若 最后一个二进制串 转换为 byte 整数时 为 负数,则其符号位肯定为 1,肯定满足 8 位,此时记录 有效位数为 8 位。 若 最后一个二进制串 转换为 非负数,则其 解码时 前面的 0 会省略,此时先将其 高位补 0,然后根据最后一个 字节记录的 有效位数 去截取即可。 比如: 0101 转为 byte 整数 5,则额外增加一个字节整数 4,表示有效位数为 4 位。 00101 转为 byte 整数 5,则额外增加一个字节整数 5,表示有效位数为 5 位。 10000101 转为 byte 整数 -123,则额外增加要给字节整数 8,表示有效位数为 8 位。 注: 由于 0 会被省略,所以需要对 非负数 进行 高位补位,即 0101 需要变为 00000101。 可以与 256 进行 按位与运算,即 5 | 256 = 0101 | 100000000 = 100000101, 此时截取 后 8 位二进制串即为 补位成功的 二进制串。 此时,对于 0101,其有效位数为 4 位,即截取 后四位 二进制串。 对于 00101,其有效位数为 5 位,即截取 后五为 二进制串。
(3)哈夫曼如何 压缩、解压
【压缩文件的流程:】 Step1:读取文件,根据文件中 字节(字符) 出现的频率 作为权值,构建出 哈夫曼树。 将 字节 频率按 从小到大 排序,并构建 哈夫曼树。 Step2:通过 哈夫曼树,可以得到每个 字节 的唯一编码。 将指向左子节点分支命名为 0,指向右子节点分支命名为 1, 则从根节点 到 某个节点的路径 记为 该节点的 编码(比如:00,010,001 等)。 Step3:使用编码 去替换掉 字节。 将文件中所有的 字节 替换成 二进制编码。 Step4:将 8 位二进制 作为一个字节 进行转码,转成字节数组 进行存储, 最后一个 二进制串 不足 8 位时按 8 位处理,并额外增加一个字节用于记录其实际位数。 Step5:将 字节数组 以及 编码表 同时 输出到文件中(完成压缩)。 【解压文件的流程:】 Step1:读取文件中的 字节数组 以及 编码表。 Step2:将 字节数组 转为对应 的二进制串。 Step3:根据编码表 得到解码表,并根据 解码表 将 二进制串 转为字符。 Step4:输出到文件即可。

(3)代码实现
【代码实现:】 package com.lyh.tree; import java.io.*; import java.util.*; public class HuffmanCode { private Map<Byte, String> huffmanCodes = new HashMap<>(); // 用于保存 编码集,字节为 key,编码为 value private Map<String, Byte> huffmanDeCodes = new HashMap<>(); // 用于保存 解码集,字节为 value,编码为 key public static void main(String[] args) { // 测试 普通字符串 test(); // 测试读取、压缩文件 // String srcFile = "G:/1.pdf"; // String zipFile = "G:/zip.pdf"; // String unzipFile = "G:/unzip.pdf"; // testZipFile(srcFile, zipFile); // testUnzipFile(zipFile, unzipFile); } /** * 测试文件 压缩 */ public static void testZipFile(String srcFile, String zipFile) { FileInputStream fis = null; OutputStream os = null; ObjectOutputStream oos = null; try { // 读取文件,将文件转为 对应的字节数组 fis = new FileInputStream(srcFile); byte[] b = new byte[fis.available()]; fis.read(b); // 根据 字节数组 生成 哈夫曼树 以及 哈夫曼编码,根据 哈夫曼编码将 原字节数组 压缩 成新的字节数组 HuffmanCode huffmanCode = new HuffmanCode(); byte[] zipResult = huffmanCode.zipFile(b); // 输出文件,将 字节数组 输出到文件中,以对象的形式存储 数据,方便读取。 os = new FileOutputStream(zipFile); oos = new ObjectOutputStream(os); // 记录压缩后的字节数组 oos.writeObject(zipResult); // 记录编码集 oos.writeObject(huffmanCode.huffmanCodes); } catch (Exception e) { System.out.println("文件操作异常"); } finally { try { fis.close(); oos.close(); os.close(); } catch (IOException e) { System.out.println("文件关闭失败"); } } } /** * 测试文件 解压 */ public static void testUnzipFile(String srcFile, String unzipFile) { InputStream is = null; ObjectInputStream ois = null; FileOutputStream fos = null; try { // 读取文件,将文件转为 对应的 字节数组 以及 哈夫曼编码 is = new FileInputStream(srcFile); ois = new ObjectInputStream(is); // 读取 字节数组 byte[] b = (byte[])ois.readObject(); // 读取 编码集 Map<Byte, String> codes = (Map<Byte, String>) ois.readObject(); // 根据 编码集 将 字节数组 解码,得到解压后的数组 HuffmanCode huffmanCode = new HuffmanCode(); huffmanCode.huffmanCodes = codes; byte[] unzipResult = huffmanCode.deCompressAndConvert(b); // 将解压后的数组写入文件 fos = new FileOutputStream(unzipFile); fos.write(unzipResult); } catch (Exception e) { System.out.println("文件操作异常"); } finally { try { ois.close(); is.close(); fos.close(); } catch (Exception e) { System.out.println("文件"); } } } /** * 测试 压缩、解压 普通字符串 * Step1:读取 普通字符串 转为字节数组, * Step2:根据字节数组 构建 哈夫曼树, * Step3: 根据 哈夫曼树 得到 所有叶子节点的 编码,组成编码集。 */ public static void test() { // 将字符转为 字节数组,并生成对应的 哈夫曼树 HuffmanCode huffmanCode = new HuffmanCode(); String data = "Java C++"; TreeNode5 root = huffmanCode.createHuffman(data.getBytes()); System.out.println("当前字符串为: " + data); System.out.println("转为字节数组为: " + Arrays.toString(data.getBytes())); // 前序遍历输出 哈夫曼树 System.out.println("字节数组转哈夫曼树后,前序遍历输出哈夫曼树: "); root.prefixList(); System.out.println("\n==============================="); // 根据 哈夫曼树,生成 字节对应的 编码表 huffmanCode.getCodes(root); System.out.println("输出当前哈夫曼树 叶子节点 对应的编码表: "); huffmanCode.hufumanCodesList(); System.out.println("\n==============================="); // 根据编码集,将 字符串对应的字节数组 转为 二进制,并以 8 位为单位 进一步转为 字节数组存储 System.out.println("压缩前的字节数组为: " + Arrays.toString(data.getBytes())); byte[] result = huffmanCode.convertAndCompress(data.getBytes()); System.out.println("压缩后的字节数组为: " + Arrays.toString(result)); System.out.println("\n==============================="); // 解压字节数组 byte[] newReult = huffmanCode.deCompressAndConvert(result); System.out.println("解压后的字节数组为: " + Arrays.toString(newReult)); System.out.println("解压后的字符串为:" + new String(newReult)); } /** * 压缩文件 * @param arrays 待压缩字节数组 * @return 压缩后的字节数组 */ public byte[] zipFile(byte[] arrays) { // 根据字节数组 字节出现频率 构建 哈夫曼树,根据 哈夫曼树 生成对应的 哈夫曼编码 getCodes(createHuffman(arrays)); // 根据 哈夫曼编码 将字节数组 对应的字节 转为 二进制串,二进制串 以 8 位为单位再转为 字节数组存储 return convertAndCompress(arrays); } /** * 解压文件 * @param arrays 待解压字节数组 * @return 解压后的字节数组 */ public byte[] unzipFile(byte[] arrays) { return deCompressAndConvert(arrays); } /** * 构建哈夫曼树 * @param arrays 字节数组 * @return 哈夫曼树根节点 */ public TreeNode5 createHuffman(byte[] arrays) { // 遍历字节数组,记录 每个字节 出现的频率作为 权值,使用 哈希表,key 存字节,value 存字节出现频率 Map<Byte, Long> map = new HashMap<>(); for (byte temp : arrays) { map.put(temp, map.getOrDefault(temp, 0L) + 1); } // 根据 权值 创建树节点 List<TreeNode5> lists = new ArrayList<>(); for (Map.Entry<Byte, Long> temp : map.entrySet()) { lists.add(new TreeNode5(temp.getKey(), temp.getValue())); } // Collections.sort(lists); // System.out.println("权值集合为: " + lists); // System.out.println("==============================="); // 遍历构建 哈夫曼树 while(lists.size() > 1) { // 排序,从小到大排序(即 哈夫曼树 左子节点权值 小于 右子节点) Collections.sort(lists); // 获取左子节点 TreeNode5 leftNode = lists.get(0); // 获取右子节点 TreeNode5 rightNode = lists.get(1); // 创建二叉树(此处非叶子节点 值为 null,只含有权值) TreeNode5 parentNode = new TreeNode5(null, leftNode.value + rightNode.value); parentNode.left = leftNode; parentNode.right = rightNode; // 移除已使用节点,添加新节点 lists.remove(leftNode); lists.remove(rightNode); lists.add(parentNode); } // 返回哈夫曼树根节点 return lists.get(0); } /** * 获取 哈夫曼树 所有 叶子节点 的路径,即 编码字符串。 * 规定:左分支为 0,右分支 为 1. * @param node 哈夫曼树根节点 */ public void getCodes(TreeNode5 node, String code, StringBuilder stringBuilder) { // 构建一个新的 StringBuilder 用于拼接字符串,当某次递归方法调用结束后,此变量作用域会消失,即不会影响之前的 StringBuilder StringBuilder stringBuilder2 = new StringBuilder(stringBuilder); stringBuilder2.append(code); // 判断当前节点是否为 空 if (node != null) { // 若当前节点值不为 null,即为 叶子节点 if (node.data != null) { // 保存到 编码集 中 huffmanCodes.put(node.data, stringBuilder2.toString()); } else { // 递归遍历左子树(左子节点),左分支为 0 getCodes(node.left, "0", stringBuilder2); // 递归遍历右子树(右子节点),右分支为 1 getCodes(node.right, "1", stringBuilder2); } } } /** * 重载 获取 编码集方法,根据 根节点 遍历 哈夫曼树 * @param root 哈夫曼树根节点 */ public void getCodes(TreeNode5 root) { getCodes(root, "", new StringBuilder()); } /** * 根据 编码集 得到 解码集 * @param huffmanCodes 解码集 */ public void getDeCodes(Map<Byte, String> huffmanCodes) { for (Map.Entry<Byte, String> temp : huffmanCodes.entrySet()) { huffmanDeCodes.put(temp.getValue(), temp.getKey()); } } /** * 输出 编码表 */ public void hufumanCodesList() { for(Map.Entry<Byte, String> map : huffmanCodes.entrySet()) { System.out.print("[ Byte = " + map.getKey() + ", String = " + map.getValue() + " ] ==> "); } } /** * 输出 解码表 */ public void hufumanDeCodesList() { for(Map.Entry<String, Byte> map : huffmanDeCodes.entrySet()) { System.out.print("[ String = " + map.getKey() + ", Byte = " + map.getValue() + " ] ==> "); } } /** * 将 字符串 对应的字节数组,根据 编码表 转为 对应的 二进制串。 * 将 二进制串 以 8 位为 一个单位,进一步转为 字节数组 * @param arrays 待压缩的字节数组(字符串转换的字节数组) * @return 压缩后的字节数组 */ public byte[] convertAndCompress(byte[] arrays) { // 根据 编码表,将 字节数组 转为对应的 二进制串 并 拼接 StringBuilder stringBuilder = new StringBuilder(); for (byte temp : arrays) { stringBuilder.append(huffmanCodes.get(temp)); } // System.out.println("转换的二进制串为: " + stringBuilder.toString()); // 以 8 位二进制为单位,将 二进制串 转为字节数组,不足 8 位 按 8 位处理,并额外增加一个字节用于记录其实际长度。 // byte[] result = new byte[stringBuilder.length() % 8 == 0 ? stringBuilder.length() / 8 : stringBuilder.length() / 8 + 1]; byte[] result = new byte[(stringBuilder.length() + 7) / 8 + 1]; for(int i = 0, j = 0; i < result.length && j < stringBuilder.length(); i++, j += 8) { if (j + 8 < stringBuilder.length()) { /** * 整数使用 补码 的形式存储, * 正数的 补码、反码、原码 均相同。 * 负数的 补码为 反码 加 1。 * 反码为 符号位不变,其余各位取反。 * 比如: 1110 0110,其符号位为 1,表示负数,则其转为整数后 为 其反码 加 1,即 1001 1010,即 -26 */ result[i] = (byte)Integer.parseInt(stringBuilder.substring(j, j + 8), 2); } else { // 额外增加一个字节用于记录其实际长度,若 恰好为 8 位,则记录 8 位,否则 记录 1 ~ 7 result[i] = (byte)Integer.parseInt(stringBuilder.substring(j), 2); result[i + 1] = (byte)stringBuilder.substring(j).length(); } } return result; } /** * 将压缩后的字节数组 转为 二进制字符串,并根据 编码表(解码表) 转为 字节数组 * @param arrays 压缩后的字节数组 * @return 解压后的字节数组 */ public byte[] deCompressAndConvert(byte[] arrays) { // 用于字符串拼接 StringBuilder stringBuilder = new StringBuilder(); // 遍历压缩后的字节数组,转为对应的 二进制 字符串 for (int i = 0; i < arrays.length - 1; i++) { /** * 使用 Integer.toBinaryString() 可以将 int 型 转为 二进制 字符串。 * 所以先将 byte 转为 int,但由于 int 为 4 字节,byte 为 1 字节,所以需要截取 int 后 8 位作为 byte 对应的 二进制字符串。 * Integer.toBinaryString() 对于非负数,其前面的 0 会默认不显示,可能造成不足 8 位的情况,所以需要对其 进行 补位。 * 比如: * Integer.toBinaryString(5) 输出为 101,但其真实对应的应该为 0000 0101, * 可以使用 5 | 256 的方式,即 101 | 1 0000 0000 进行 按位与运算。结果为 1 0000 0101,再截取 后 8 位即为对应的 二进制字符串。 * * Integer.toBinaryString() 对于负数,转换为 int 后,会显示 32 位,首位为 1,所以无需补位,直接截取低 8 位即可。 * * 倒数最后一个字节,表示 倒数第二个字节 实际转换的 二进制串 位数, * 所以 处理倒数第二个字节时,需要根据 倒数最后一个字节 进行 字符串截取操作。 */ int temp = arrays[i]; // 低 8 位 与 1 0000 0000 进行按位与运算,比如: 101 | 1 0000 0000 = 1 0000 0101 temp |= 256; String str = Integer.toBinaryString(temp); // 若当前为倒数第二个字节,则根据 倒数第一个字节 记录的值 去截取 倒数第二个字节 的实际字符串 if (i + 1 == arrays.length - 1) { stringBuilder.append(str.substring(arrays[i + 1] + 1)); } else { stringBuilder.append(str.substring(str.length() - 8)); } } // 根据 编码集 得到 解码集 getDeCodes(huffmanCodes); System.out.println("输出编码表 对应的 解码表: "); hufumanDeCodesList(); System.out.println("\n==============================="); // 保存转换的二进制字符串 List<Byte> list = new ArrayList<>(); // 根据解码集,将 二进制字符串 转换成 字节数组 for(int i = 0, j = 1; j <= stringBuilder.length(); j++) { Byte temp = huffmanDeCodes.get(stringBuilder.substring(i, j)); if (temp != null) { list.add(temp); i = j; } } // 第一种返回方式:Byte[] newResult = list.toArray(new Byte[list.size()]); // 第二种返回方式: byte[] result = new byte[list.size()]; for(int i = 0; i < list.size(); i++) { result[i] = list.get(i); } return result; } } /** * 定义树节点 */ class TreeNode5 implements Comparable<TreeNode5> { Byte data; // 保存节点数据 Long value; // 保存节点权值(字符出现频率) TreeNode5 left; // 保存左子节点 TreeNode5 right; // 保存右子节点 @Override public int compareTo(TreeNode5 o) { return (int)(this.value - o.value); } public TreeNode5(Byte data, Long value) { this.data = data; this.value = value; } @Override public String toString() { return "TreeNode5{ data = " + data + ", value = " + value + " }"; } /** * 前序遍历 */ public void prefixList() { // 输出当前节点 System.out.print(this + " "); // 遍历左子节点 if (this.left != null) { this.left.prefixList(); } // 遍历右子节点 if (this.right != null) { this.right.prefixList(); } } } 【输出结果:】 当前字符串为: Java C++ 转为字节数组为: [74, 97, 118, 97, 32, 67, 43, 43] 字节数组转哈夫曼树后,前序遍历输出哈夫曼树: TreeNode5{ data = null, value = 8 } TreeNode5{ data = null, value = 4 } TreeNode5{ data = 97, value = 2 } TreeNode5{ data = 43, value = 2 } TreeNode5{ data = null, value = 4 } TreeNode5{ data = null, value = 2 } TreeNode5{ data = 32, value = 1 } TreeNode5{ data = 67, value = 1 } TreeNode5{ data = null, value = 2 } TreeNode5{ data = 118, value = 1 } TreeNode5{ data = 74, value = 1 } =============================== 输出当前哈夫曼树 叶子节点 对应的编码表: [ Byte = 32, String = 100 ] ==> [ Byte = 97, String = 00 ] ==> [ Byte = 67, String = 101 ] ==> [ Byte = 118, String = 110 ] ==> [ Byte = 74, String = 111 ] ==> [ Byte = 43, String = 01 ] ==> =============================== 压缩前的字节数组为: [74, 97, 118, 97, 32, 67, 43, 43] 压缩后的字节数组为: [-26, 37, 5, 4] =============================== 输出编码表 对应的 解码表: [ String = 00, Byte = 97 ] ==> [ String = 110, Byte = 118 ] ==> [ String = 100, Byte = 32 ] ==> [ String = 111, Byte = 74 ] ==> [ String = 01, Byte = 43 ] ==> [ String = 101, Byte = 67 ] ==> =============================== 解压后的字节数组为: [74, 97, 118, 97, 32, 67, 43, 43] 解压后的字符串为:Java C++
9、二叉排序树(二叉搜索树、BST)
(1)什么是 BST?
BST 可以是 Binary Sort Tree 的缩写(二叉排序树),也可以是 Binary Search Sort 的缩写(二叉搜索树)。其查询效率 相比于 链式结构 高。
【BST 特点:】
对于一颗二叉树,其满足如下定义:
任何一个非叶子节点,其左子节点的值 小于 当前节点。
任何一个非叶子节点,其右子节点的值 大于 当前节点。
注:
若存在 节点相等的情况,可以将该节点 放在 左子节点 或者 右子节点 处。
即 二叉排序树可能存在三种定义:
左子节点 小于等于 当前节点,右子节点 大于 当前节点。
左子节点 小于 当前节点,右子节点 大于等于 当前节点。
左子节点 小于 当前节点,右子节点 大于 当前节点。

(2)BST 增、删、查 操作
此处规定 左子节点 小于 当前节点,右子节点 大于等于 当前节点。
【添加节点:】 若 待添加节点 小于 当前节点,则 递归向 当前节点 左子节点 进行添加操作。 若 待添加节点 大于等于 当前节点,则 递归向 当前节点 右子节点 进行添加操作。 【查找节点:】 若 待查找节点 等于 当前节点,则 查找成功。 若 待查找节点 小于 当前节点,则 递归向 左子节点 查找。 若 待查找节点 大于等于 当前节点,则 递归向 右子节点 查找。 【删除节点:】 删除节点可能存在三种情况: 删除的是 叶子节点。 删除的是 非叶子节点,且 只有一个子节点。 删除的是 非叶子节点,且 有两个子节点。 若删除的是 叶子节点: Step1:先去查找需要删除的节点是否存在,存在则进行下面操作。 Step2:若删除节点为 根节点,则根节点直接置 null。即 root = null; Step3:若删除节点不是 根节点,则 找到 待删除节点的 父节点, 若 待删除节点为 父节点 的 左子节点,则将左子节点置 null。即 parent.left = null; 若 待删除节点为 父节点 的 右子节点,则将右子节点置 null。即 parent.right = null; 若删除的是 非叶子节点,且 只有一个子节点。 Step1 同上。 Step2:若删除节点为 根节点,则根节点直接指向 子节点即可。 Step3:找到 待删除节点的 父节点,并判断 待删除节点 子节点 是 左子节点 还是 右子节点。 若 待删除节点为 父节点 的 左子节点,且 待删除节点 存在 左子节点,则 父节点的 左子节点 直接指向 删除节点的左子节点。即 parent.left = node.left; 若 待删除节点为 父节点 的 左子节点,且 待删除节点 存在 右子节点,则 父节点的 左子节点 直接指向 删除节点的右子节点。即 parent.left = node.right; 若 待删除节点为 父节点 的 右子节点,且 待删除节点 存在 左子节点,则 父节点的 右子节点 直接指向 删除节点的左子节点。即 parent.right = node.left; 若 待删除节点为 父节点 的 右子节点,且 待删除节点 存在 右子节点,则 父节点的 右子节点 直接指向 删除节点的右子节点。即 parent.right = node.right; 若删除的是 非叶子节点,且 有两个子节点。 Step1 同上。 Step2:找到 待删除节点,并找到 其右子树最小值 或者 左子树最大值, 删除找到的节点,并将其值置于 待删除节点处。 即 保证将 左子树 的最大值 放置到 中间节点 或者 将 右子树 最小值 放到中间节点。 使得 左子树的所有节点 小于 中间节点, 右子树的所有节点 大于等于 中间节点。 【代码实现:】 package com.lyh.tree; import java.util.ArrayList; import java.util.Arrays; import java.util.List; public class BinarySearchTree { private TreeNode7 root; // 设置根节点 public static void main(String[] args) { // 构造二叉排序树 BinarySearchTree binarySearchTree = new BinarySearchTree(); int[] arrays = new int[]{7, 3, 10, 12, 5, 1, 9}; for (int temp : arrays) { binarySearchTree.addNote(temp); } // 输出原数组 System.out.println("原数组为: " + Arrays.toString(arrays)); System.out.println("======================================"); // 输出中序遍历结果 System.out.println("二叉排序树中序遍历结果为: " + binarySearchTree.infixList()); System.out.println("======================================"); // 输出查找结果 System.out.println("查找 10: " + binarySearchTree.search(10)); System.out.println("查找 20: " + binarySearchTree.search(20)); System.out.println("查找 9: " + binarySearchTree.search(9)); System.out.println("======================================"); // 输出查找节点的父节点 System.out.println("查找 9: " + binarySearchTree.searchParent(9)); System.out.println("查找 7: " + binarySearchTree.searchParent(7)); System.out.println("======================================"); // 输出删除后的 二叉搜索树 for (int i = 0; i < arrays.length; i++) { System.out.println("删除 " + arrays[i] + " : " + binarySearchTree.deleteNode(arrays[i])); System.out.println("二叉排序树中序遍历结果为: " + binarySearchTree.infixList()); System.out.println("======================================"); } } /** * 添加节点 * @param data 数据 */ public void addNote(int data) { if (root == null) { root = new TreeNode7(data); return; } root.addNode(new TreeNode7(data)); } /** * 中序遍历 * @return 中序遍历结果 */ public List infixList() { if (root == null) { System.out.println("为空树"); return null; } return root.infixList(new ArrayList()); } /** * 查找节点 * @param data 待查找数据 * @return 若查找失败返回 null */ public TreeNode7 search(int data) { // 根节点不存在时,返回 null if (root == null) { return null; } return root.search(data); } /** * 查找节点的父节点 * @param data 待查找数据 * @return 若查找失败返回 null */ public TreeNode7 searchParent(int data) { // 根节点不存在时,返回 null if (root == null) { return null; } return root.searchParent(data); } /** * 删除节点 * @param data 待删除节点 * @return 删除失败返回 -1,删除成功返回 0 */ public int deleteNode(int data) { // 先查找 待删除节点 是否存在 TreeNode7 node = search(data); // 删除节点存在,则进行删除操作 if (node != null) { // 查找待删除节点的父节点 TreeNode7 parent = searchParent(data); // 删除节点不为根节点时, // 若删除的是 叶子节点,则判断当前 删除节点为 父节点的左子节点 还是 右子节点 if (node.left == null && node.right == null) { // parent 为空,则删除节点为 根节点,直接将 根节点置 null if (parent == null) { root = null; return 0; } if (parent.left != null && parent.left.data == data) { parent.left = null; } else { parent.right = null; } return 0; } // 若删除的是 非叶子节点,且只有一个 左子节点。 if (node.left != null && node.right == null) { // parent 为空,则删除节点为 根节点,直接赋值为 左子节点 即可 if (parent == null) { root = node.left; return 0; } // 若待删除节点为 父节点的左子节点 if (parent.left != null && parent.left.data == data) { parent.left = node.left; } else { // 若 待删除节点为 父节点的 右子节点 parent.right = node.left; } return 0; } // 若删除的是 非叶子节点,且只有一个 右子节点 if (node.right != null && node.left == null) { // parent 为空,则删除节点为 根节点,直接赋值为 右子节点 即可 if (parent == null) { root = node.right; return 0; } // 若待删除节点为 父节点的左子节点 if (parent.left != null && parent.left.data == data) { parent.left = node.right; } else { // 若 待删除节点为 父节点的 右子节点 parent.right = node.right; } return 0; } // 若删除的是 非叶子节点,且有两个 子节点 // 找到 右子树 最小值,并覆盖 待删除节点,则满足 二叉搜索树条件 TreeNode7 minRightNode = node.right; while(minRightNode.left != null) { minRightNode = minRightNode.left; } // 记录 右子树最小值 int minRightData = minRightNode.data; // 删除 右子树最小值 deleteNode(minRightData); // 将最小值 覆盖 待删除节点,即完成 删除操作 node.data = minRightData; return 0; } // 删除节点不存在,返回 -1,表示删除失败 return -1; } } /** * 定义树节点 */ class TreeNode7 { int data; // 保存节点数据 TreeNode7 left; // 保存 左子节点 TreeNode7 right; // 保存 右子节点 public TreeNode7(int data) { this.data = data; } @Override public String toString() { return "TreeNode7{ data = " + data + ", left = " + left + ", right = " + right + " }"; } /** * 中序遍历 * @param result 中序遍历结果 * @return 中序遍历结果 */ public List infixList(List result) { // 递归遍历 左子节点 if (this.left != null) { this.left.infixList(result); } // 保存 当前节点 result.add(this.data); // 递归遍历 右子节点 if (this.right != null) { this.right.infixList(result); } return result; } /** * 添加节点 * @param node 节点 */ public void addNode(TreeNode7 node) { // 节点不存在时,不添加 if (node == null) { return; } // 节点存在时 if (this.data > node.data) { // 数据小于当前节点时,在左子树进行添加 if (this.left != null) { this.left.addNode(node); } else { this.left = node; } } else { // 数据大于等于当前节点是,在右子树进行添加 if (this.right != null) { this.right.addNode(node); } else { this.right = node; } } } /** * 查找节点 * @param data 待查找数据 * @return 查找失败返回 null */ public TreeNode7 search(int data) { // 当前节点 即为 待查找节点 if (this.data == data) { return this; } // 若 当前节点 大于 待查找节点,则递归左子树进行查找 if (this.data > data && this.left != null) { return this.left.search(data); } // 若 当前节点 小于等于 待查找节点,则递归右子树进行查找 if (this.data <= data && this.right != null) { return this.right.search(data); } // 查找失败返回 null return null; } /** * 查找节点 * @param data 待查找数据 * @return 查找失败返回 null */ public TreeNode7 searchParent(int data) { // 若当前节点 左子树 或者 右子树 查找数据成功,返回 当前节点 if ((this.left != null && this.left.data == data) || (this.right != null && this.right.data == data)) { return this; } // 若 当前节点 大于 待查找节点,则递归 左子树查找 if (this.data > data && this.left != null) { return this.left.searchParent(data); } // 若 当前节点 小于等于 待查找节点,则递归 右子树查找 if (this.data <= data && this.right != null) { return this.right.searchParent(data); } // 查找失败,返回 null return null; } } 【输出结果:】 原数组为: [7, 3, 10, 12, 5, 1, 9] ====================================== 二叉排序树中序遍历结果为: [1, 3, 5, 7, 9, 10, 12] ====================================== 查找 10: TreeNode7{ data = 10, left = TreeNode7{ data = 9, left = null, right = null }, right = TreeNode7{ data = 12, left = null, right = null } } 查找 20: null 查找 9: TreeNode7{ data = 9, left = null, right = null } ====================================== 查找 9: TreeNode7{ data = 10, left = TreeNode7{ data = 9, left = null, right = null }, right = TreeNode7{ data = 12, left = null, right = null } } 查找 7: null ====================================== 删除 7 : 0 二叉排序树中序遍历结果为: [1, 3, 5, 9, 10, 12] ====================================== 删除 3 : 0 二叉排序树中序遍历结果为: [1, 5, 9, 10, 12] ====================================== 删除 10 : 0 二叉排序树中序遍历结果为: [1, 5, 9, 12] ====================================== 删除 12 : 0 二叉排序树中序遍历结果为: [1, 5, 9] ====================================== 删除 5 : 0 二叉排序树中序遍历结果为: [1, 9] ====================================== 删除 1 : 0 二叉排序树中序遍历结果为: [9] ====================================== 删除 9 : 0 为空树 二叉排序树中序遍历结果为: null ======================================
10、平衡二叉树(AVL)
(1)什么是 平衡二叉树?
平衡二叉树(Balanced Binary Tree)也称为 自平衡二叉搜索树(Self Balanced Binary Search Tree),也称为 AVL 树(人名缩写)。用于提高 二叉搜索树 的查询效率。
其本质上 仍是 一颗 二叉搜索树,只是其会自动 旋转节点(平衡条件),用于保证 树的高度。
平衡条件:
每个节点 的 左、右子树 的高度差的绝对值 不超过 1。且 左、右两个子树 也是 平衡二叉树。
普通 二叉搜索树 构建如下:
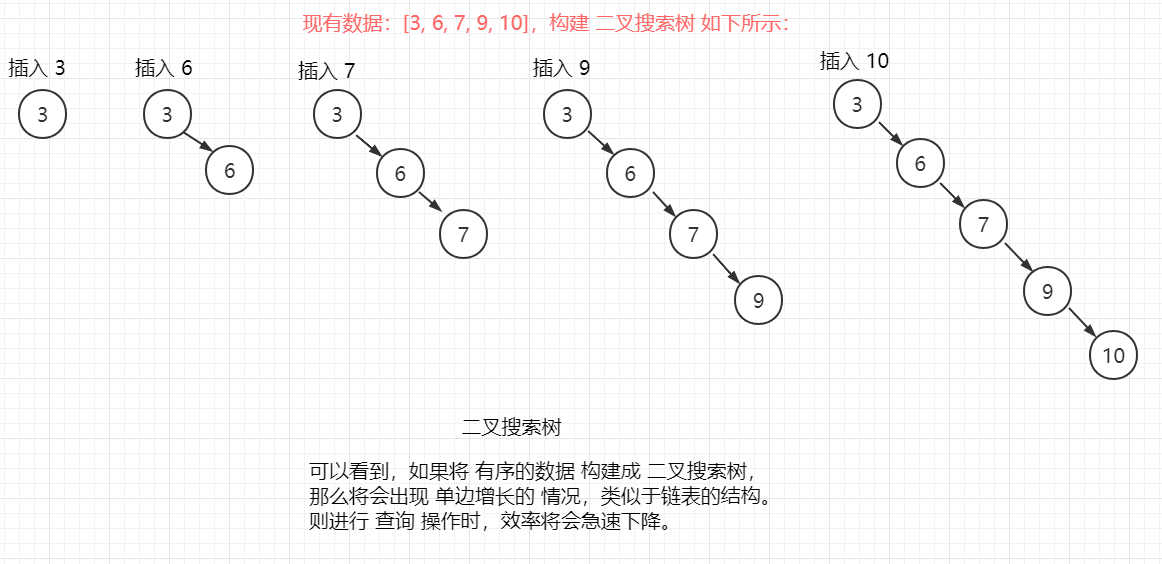
平衡二叉搜索树构建如下:
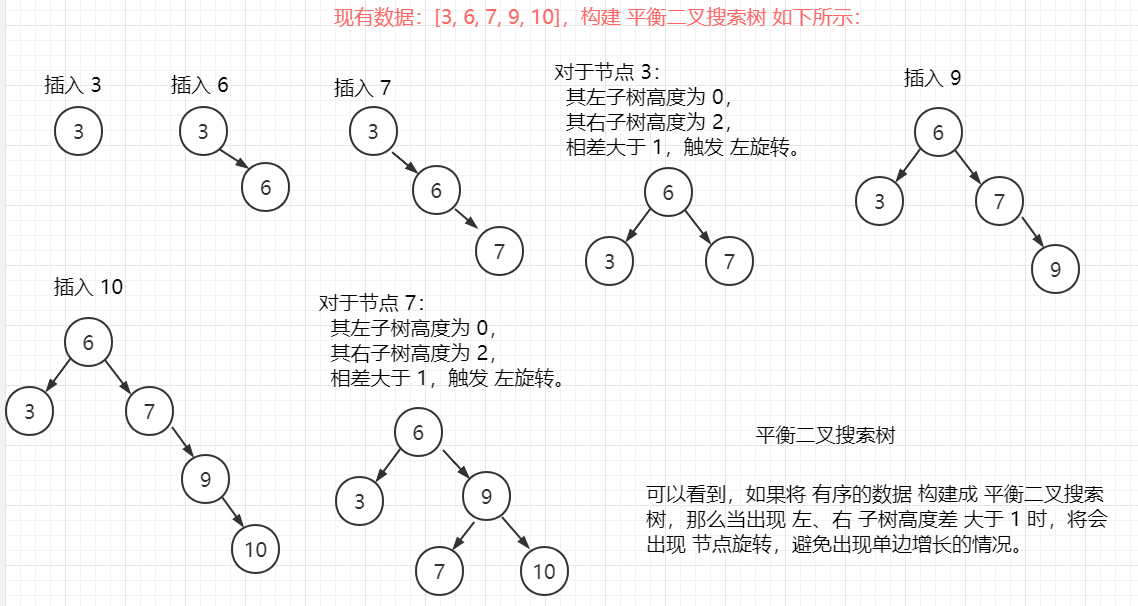
(2)如何实现平衡?
当 左、右子树 出现高度差 大于 1 时,为了实现平衡,节点需要进行旋转。
【节点的 高度、深度:(此处仅个人理解,有不对的地方还望不吝赐教)】 当前节点的高度:从 当前节点 开始 到 叶子节点 最长路径 的节点数。 当前节点的深度:从 根节点 开始 到当前节点 最长路径 的节点数。 注: 此处假定 节点不存在时为 0。节点存在记为 1。 虽然树的 高度、深度相同,但具体到 某个节点的 高度、深度 不一定相同。 比如: A B C E F G 如上图所示, B 节点 高度为 3(B->E->G,3个节点),深度为 2(A->B,2个节点)。 C 节点高度为 2(C->F,2个节点),深度为 2(A->C,两个节点)。 【旋转类型:】 左旋转。 右旋转。 双旋转(左旋转、右旋转)。 【左旋转:】 左子树高度 小于 右子树高度,且 高度差 大于 1, 此时 需要将 右子树节点 向左旋转,降低 右子树的高度。 步骤(某个节点需要旋转时): Step1:创建一个新的节点,用于保存 当前节点的值。 Step2:将新节点的左子树 设置成 当前节点的 左子树。 Step3:将新节点的右子树 设置成 当前节点的 右子树的左子树。 Step4:将当前节点的值 设置成 右子树根节点的值。 Step5:将当前节点的右子树 设置成 右子树的右子树。 Step6:将当前节点的左子树 设置成 新节点。 【右旋转:】 左子树高度 大于 右子树高度,且 高度差 大于 1, 此时 需要将 左子树节点 向右旋转,降低 左子树的高度。 步骤(某个节点需要旋转时): Step1:创建一个新的节点,用于保存 当前节点的值。 Step2:将新节点的右子树 设置成 当前节点的 右子树。 Step3:将新节点的左子树 设置成 当前节点的 左子树的右子树。 Step4:将当前节点的值 设置成 左子树根节点的值。 Step5:将当前节点的左子树 设置成 右子树的左子树。 Step6:将当前节点的右子树 设置成 新节点。 【单一 左旋转、右旋转 出现的问题:】 只存在 左旋转、右旋转时,可能造成 死循环。需要两者结合使用。 比如: 插入节点 C 如下: A B C A 节点右子树高度为 2,左子树高度为 1,需要进行 左旋转。 左旋转后: B A C 此时,B 节点左子树高度为 2,右子树高度为 1,需要进行 右旋转。 右旋转后: A B C 发现右旋转后,又回到了最初的起点。从而出现死循环。 【双旋转:】 结合左旋转、右旋转。 先旋转 子节点,再旋转 当前节点。 步骤(存在两种情况): 情况一(当前节点符合右旋转时): 若当前节点 左子树 的 右子树的高度 大于 左子树 的 左子树的高度, 则先 对 当前节点的 左节点 进行 左旋转。 然后再 对当前节点 进行 右旋转。 情况二(当前节点符合左旋转时): 若当前节点 右子树 的 左子树的高度 大于 右子树的 右子树的高度, 则 先对 当前节点的 右节点 进行 右旋转。 然后再 对当前节点进行左旋转。
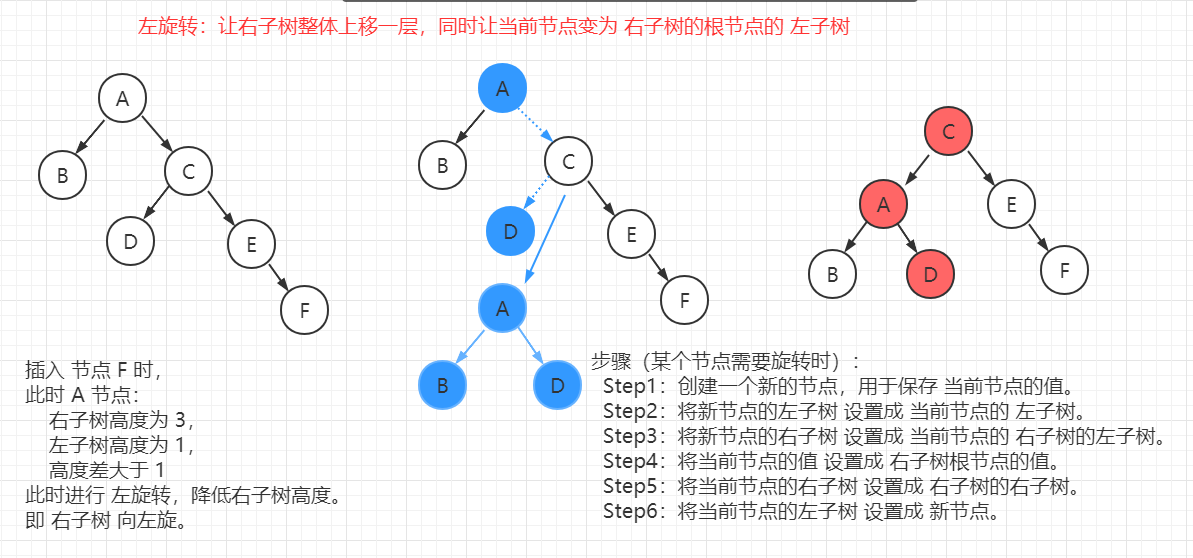
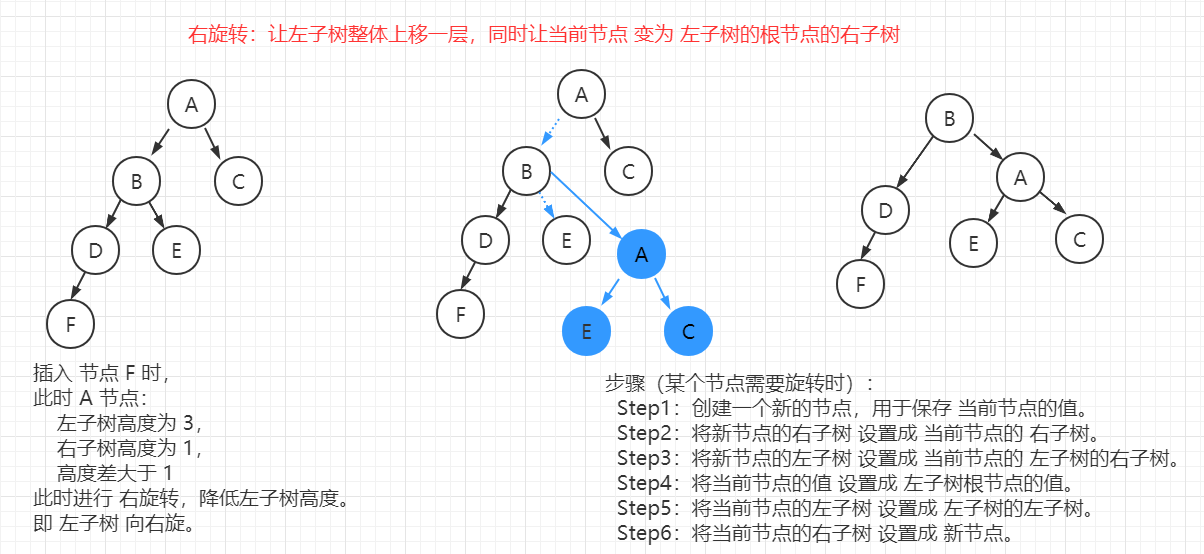


(3)代码实现
【代码实现:】 package com.lyh.tree; import java.util.ArrayList; import java.util.Arrays; import java.util.List; public class BalanceBinarySearchTree { private TreeNode8 root; // 设置根节点 public static void main(String[] args) { int[] arrays = new int[]{3, 6, 7, 9, 10}; // int[] arrays = new int[]{10, 11, 7, 6, 8, 9}; System.out.println("原数组为: " + Arrays.toString(arrays)); System.out.println("====================================="); // 构建普通的 二叉搜索树 System.out.println("构建普通 二叉搜索树:"); BalanceBinarySearchTree balanceBinarySearchTree2 = new BalanceBinarySearchTree(); for (int temp : arrays) { balanceBinarySearchTree2.addNote2(temp); } System.out.println("中序遍历为: " + balanceBinarySearchTree2.infixList()); // 输出根节点、以及根节点高度 System.out.println(balanceBinarySearchTree2.root); System.out.println(balanceBinarySearchTree2.root.getHeight()); System.out.println("====================================="); // 构建 平衡二叉树 System.out.println("构建平衡二叉树:"); BalanceBinarySearchTree balanceBinarySearchTree = new BalanceBinarySearchTree(); for (int temp : arrays) { balanceBinarySearchTree.addNote(temp); } System.out.println("中序遍历为: " + balanceBinarySearchTree.infixList()); // 输出根节点、以及根节点高度 System.out.println(balanceBinarySearchTree.root); System.out.println(balanceBinarySearchTree.root.getHeight()); System.out.println("====================================="); } /** * 添加节点(平衡二叉搜索树 添加节点的方式,节点会旋转) * @param data 数据 */ public void addNote(int data) { if (root == null) { root = new TreeNode8(data); return; } root.addNode(new TreeNode8(data)); } /** * 添加节点(普通 二叉搜索树 添加节点的方式) * @param data 数据 */ public void addNote2(int data) { if (root == null) { root = new TreeNode8(data); return; } root.addNode2(new TreeNode8(data)); } /** * 中序遍历 * @return 中序遍历结果 */ public List infixList() { if (root == null) { System.out.println("为空树"); return null; } return root.infixList(new ArrayList()); } } /** * 定义树节点 */ class TreeNode8 { int data; // 保存节点数据 TreeNode8 left; // 保存 左子节点 TreeNode8 right; // 保存 右子节点 public TreeNode8(int data) { this.data = data; } @Override public String toString() { return "TreeNode8{ data = " + data + ", left = " + left + ", right = " + right + " }"; } /** * 中序遍历 * * @param result 中序遍历结果 * @return 中序遍历结果 */ public List infixList(List result) { // 递归遍历 左子节点 if (this.left != null) { this.left.infixList(result); } // 保存 当前节点 result.add(this.data); // 递归遍历 右子节点 if (this.right != null) { this.right.infixList(result); } return result; } /** * 添加节点(平衡二叉搜索树 添加节点的方式,节点会旋转) * @param node 节点 */ public void addNode(TreeNode8 node) { // 节点不存在时,不添加 if (node == null) { return; } // 节点存在时 if (this.data > node.data) { // 数据小于当前节点时,在左子树进行添加 if (this.left != null) { this.left.addNode(node); } else { this.left = node; } } else { // 数据大于等于当前节点是,在右子树进行添加 if (this.right != null) { this.right.addNode(node); } else { this.right = node; } } // 添加节点后需要判断 当前节点是否需要旋转 // 当前节点左子树高度 大于 右子树高度,且差值超过 1,则需要进行 右旋转 if (this.getLeftHeight() - this.getRightHeight() > 1) { // 当前节点 左子树 的左子节点高度 小于 左子树 的右子节点高度时,需要先对 左子树进行 左旋转 if (this.left != null && this.left.getLeftHeight() < this.left.getRightHeight()) { this.left.leftRotate(); } // 当前节点进行右旋转 this.rightRotate(); return; } // 当前节点右子树高度 大于 左子树高度,其差值超过 1,则需要进行 左旋转 if (this.getRightHeight() - this.getLeftHeight() > 1) { // 当前节点 右子树 的左子节点高度 大于 右子树 的右子节点高度时,需要先对 右子树进行 右旋转 if (this.right != null && this.right.getLeftHeight() > this.right.getRightHeight()) { this.right.rightRotate(); } // 当前节点进行左旋转 this.leftRotate(); } } /** * 添加节点(普通 二叉搜索树 添加节点的方式) * @param node 节点 */ public void addNode2(TreeNode8 node) { // 节点不存在时,不添加 if (node == null) { return; } // 节点存在时 if (this.data > node.data) { // 数据小于当前节点时,在左子树进行添加 if (this.left != null) { this.left.addNode2(node); } else { this.left = node; } } else { // 数据大于等于当前节点是,在右子树进行添加 if (this.right != null) { this.right.addNode2(node); } else { this.right = node; } } } /** * 返回节点的高度 * @return 节点的高度,节点不存在则返回 0。 */ public int getHeight() { return this == null ? 0 : Math.max(this.getLeftHeight(), this.getRightHeight()) + 1; } /** * 返回 左子树 的高度 * @return 左子树的高度 */ public int getLeftHeight() { return this.left == null ? 0 : this.left.getHeight(); } /** * 返回 右子树 的高度 * @return 右子树的高度 */ public int getRightHeight() { return this.right == null ? 0 : this.right.getHeight(); } /** * 节点进行左旋转 */ public void leftRotate() { // 创建一个新节点,并保存当前节点的值 TreeNode8 newNode = new TreeNode8(this.data); // 新节点的 左子树设置成 当前节点的左子树 newNode.left = this.left; // 新节点的 右子树设置成 当前节点的 右子树的左子树 newNode.right = this.right.left; // 当前节点的值 设置成 其右子树 根节点的值 this.data = this.right.data; // 当前节点的 左子树 设置成 新节点 this.left = newNode; // 当前节点的 右子树 设置成 其右子树的右子树 this.right = this.right.right; } /** * 节点进行右旋转 */ public void rightRotate() { // 创建一个新节点,用于保存当前节点的值 TreeNode8 newNode = new TreeNode8(this.data); // 新节点的 左子树设置成 当前节点的 左子树的右子树 newNode.left = this.left.right; // 新节点的 右子树设置成 当前节点的 右子树 newNode.right = this.right; // 当前节点的值 设置成 其左子树 根节点的值 this.data = this.left.data; // 当前节点的 左子树 设置成 其左子树的左子树 this.left = this.left.left; // 当前节点的 右子树 设置成 其右子树的右子树 this.right = newNode; } } 【输出结果:】 原数组为: [3, 6, 7, 9, 10] ===================================== 构建普通 二叉搜索树: 中序遍历为: [3, 6, 7, 9, 10] TreeNode8{ data = 3, left = null, right = TreeNode8{ data = 6, left = null, right = TreeNode8{ data = 7, left = null, right = TreeNode8{ data = 9, left = null, right = TreeNode8{ data = 10, left = null, right = null } } } } } 5 ===================================== 构建平衡二叉树: 中序遍历为: [3, 6, 7, 9, 10] TreeNode8{ data = 6, left = TreeNode8{ data = 3, left = null, right = null }, right = TreeNode8{ data = 9, left = TreeNode8{ data = 7, left = null, right = null }, right = TreeNode8{ data = 10, left = null, right = null } } } 3 =====================================
11、树的补充
Java 内功修炼 之 数据结构与算法(二):https://www.cnblogs.com/l-y-h/p/13986943.html




