数据分析:决策树
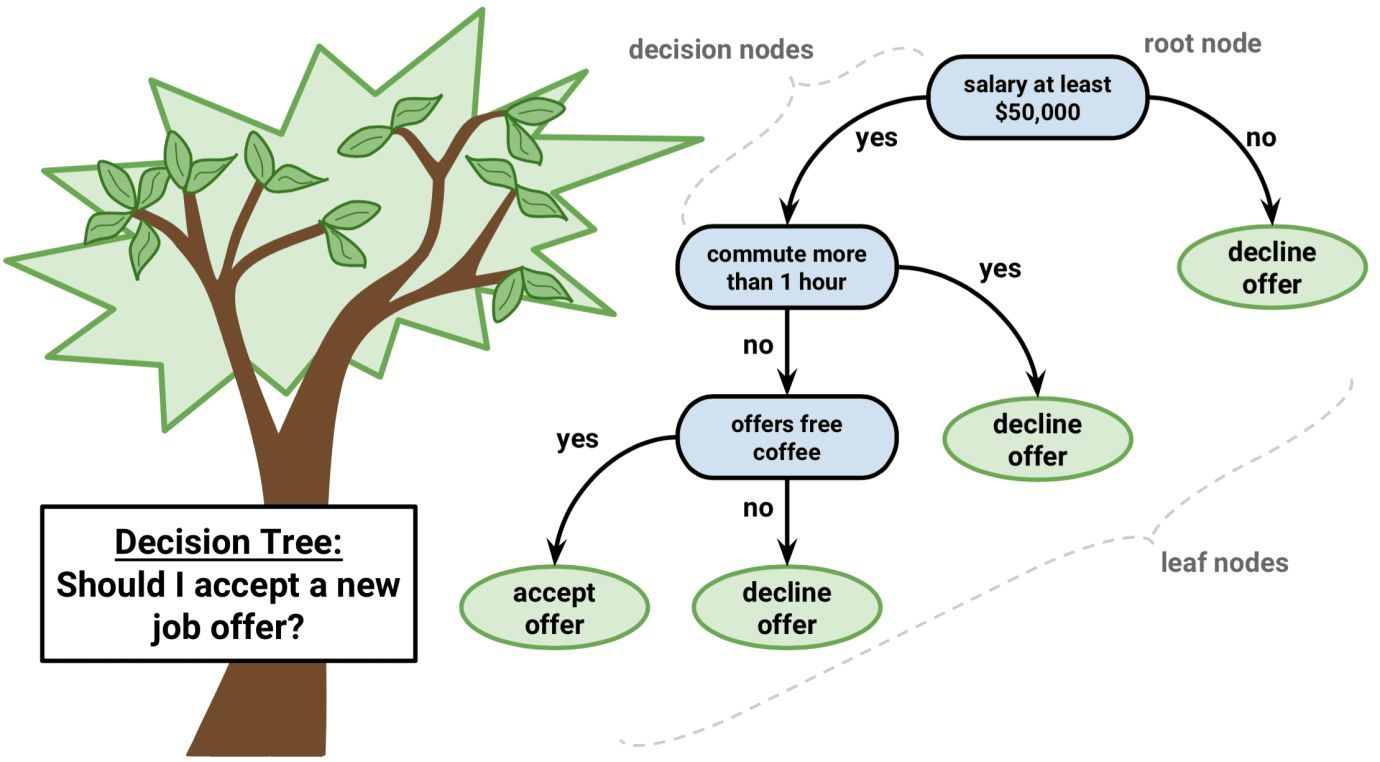
引言
高二(1)班的小明同学和小方同学为了准备即将进行的校园羽毛球大赛,准备近一个月的时间去练习打球。不过,并不是每一天都适合练球。通常,小明和小方需要考虑一些因素来决定今天是否适合打羽毛球,比如:今天是否有场地(若没有室内场地,就只能选择室外场地),如果是要在室外练习的话,天气是否合适,是否会刮风等,例如下表所示:
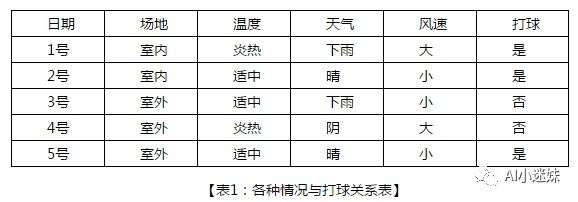
实际上,上述的问题是一个典型的智能决策问题。首先,它有一些输入的特征,比如场地是市内还是室外,气温是炎热,天气是下雨还是晴天,风速是大还是小;小明和小方通过某种特定的算法,对这一系列的特征进行综合判断,从而得出今天是否应该打球的决策。可以看到,对一个智能决策系统,它有三个重要的组成部分,即特征、算法、决策。下图体现了一个典型的智能决策系统的组成部门,以及各部分之间的输入/输出关系。
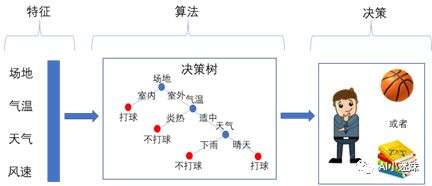
决策树
在上面的例子中,场地,天气,温度,风速特征选取完成后,开始进行决策,在我们的问题中,决策的内容实际上是将结果分成两类,即是(1)否(0)练球。这一类智能决策问题称为分类问题,决策树是一种简单的处理分类问题的算法.
决策树的本质是由多个判断节点组成的树形函数,以一个样本的特征向量X=(X1,X2,X3...Xd) 作为输入,返回一个“决策”,例如判断具有该特征的样本属于哪个类别。简单地说,我们从一个“树根“节点开始,每次生出几个(例如2)分叉节点(称为子节点),再将子节点当成新的根节点,继续往下生出新的子节点,如此重复,直到满足某些停止条件停止决策树的生长。当一棵决策树建立完毕后,我们称最下面的节点(无子节点)为叶节点。其他的节点成为非叶节点。每个非叶节点与一个特征属性相关联,根据此特征属性的值的不同,进行子节点的分叉操作。
决策树的原理
我们用下图来说明决策树的工作原理。首先我们选取天气值作为判断变量(作为根节点),根据天气可以取值(晴天、阴天、雨天)等三个值,我们的决策生成三个分叉。我们发现阴天是最适合打球的天气(因为即没有日晒,又不雨淋),因此只要是遇上阴天,我们的决策都是“打球“。此时我们的三个分叉中,相关阴天那个子节点变成了叶节点,不再往下继续生成(因为走到此节点的所有样本,都会直接被判为“打球”)。如果遇到晴天或者雨天(即样本如果走到两外两个分叉),我们并不可不可以打球,这时候需要利用另外一个特征属性进行进一步判断决策。具体的可以参考下图。
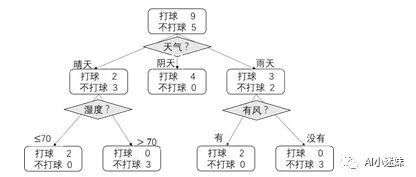
当输入一个样本X=(X1,X2,X3...Xd)后,会根据每个节点预设的特征属性以及分叉规则,走到下面一层的节点,接着根据这个新寻址到的节点的预设特征属性以及分叉规则,继续往决策树的下一层走,一直到走到某个叶节点,整个行程结束。换句话说,每个样本在决策树上都有一个唯一的,规定好的行走路线(自根节点至叶节点),在叶节点上,完成最终的决策,如分类(如可以根据走到该叶节点上的训练数据的类别标签,赋值给新的测试数据)。我们不难发现,以上决策树的工作过程,有两个关键点:
特征属性序列:在决策树的生成构建中,对于每次分叉选择那个特征属性,对最终形成决策树的分类性能有影响。例如,为什么我们要先判断天气,再判断湿度或是否有风?这个次序倒过来,是否对我们的智能决策产生影响?
特征属性形式:我们观察到,在上述的例子中,有些输入特征属性是标签型的,比如天气的三个种类(晴天、雨天、阴天),也有一些属性是连续的实数,如温度,湿度等。不同类型的属性,决策树中对应节点的分叉判断依据也是有所差别。比如对于标签类型的特征属性,我们可以按照标签的k个类型进行k个子节点分叉。具体的说,根据(Xi==晴天 或 Xi==雨天 或Xi==阴天)这几个条件来判断数据样本的走向。 对于实数类型的特征属性,我们可以进行设置阈值的操作。具体地说根据(Xi>=阈值 或Xi<= 阈值)来决定数据样本在节点走那支分叉。
决策树的构建
[使用专家规则]:根据专家的知识,人为的规定来生成决策树。先考虑哪个特征,再考虑哪个特征;同时在设置每个分叉节点的分叉条件时,可以人为地设置我们认为最合适的分叉判别条件。例如,在上述的例子中,通常打羽毛球的高手知道,我们应该先判断天气类型,然后根据天气类型,再考虑湿度,是否有风等因素,进行决策。所有的属性探索先后顺序,以及每个节点分叉条件判别式,都是事先规定好的。
[使用数据训练]:在很多情况下,我们并不具备“专家”的能力。例如对于某种分类问题,我们可以找到1000多种特征属性,显然“手动地“选择某个属性,设置分叉条件显然是不可能做到的。在这种情况下,我们通常使用大量历史数据(带有最终的分类标签)来自动地进行决策树的构建。这种方式通常称作决策树训练。决策树的训练通常是递归地,即一层下一层地训练每个树节点(选择某个属性,设置某个阈值或分叉条件),具体如下:
1)初始化一个根节点。令所有的训练样本“走“到该根节点上。
2)寻找一个合适的特征属性作为该节点往下分叉的判别变量。并且对该变量设置一个分叉判别函数。例如我们选择天气这个变量,且将判别条件设为(Xi==晴天 或 Xi==雨天 或Xi==阴天)。这里的关键问题是,如何自动地选择某个属性?这里,我们的准则是:我们所选择的特征属性(以及判别条件式子)能使得分叉的左右两边的数据样本尽量根据最终的分类标签进行分开。例如在我们的例子中,如选择了“湿度“这个属性,我们发现如果设判别阈值为70的时候,走到左边子节点的数据样本都属于”不打球“,而右边都属于”要打球“。如此,我们的期望达到了,即将数据根据最终的决策标签分开。
换句话说,在分类问题中,我们希望每一分类节点下的样例类别一致,即“纯度”较高。决策过程中,在每个节点我们都会对很多属性进行分开特性的“测试”,选取一个最佳的分开函数。即使得走到左右子节点的样本数据各自“纯度“都较高。
3) 根据刚才获得的属性选取以及分叉函数设置,将当前节点上的数据往下面的子节点推送,并重复2)的操作。即递归地进行属性选择以及判别式设置。
4)当数据达某个节点时,“纯度“达到最高(即全部都属于一个分类标签),则这个节点的生成过程结束,并设置该节点的标签为走到该节点上训练数据所带的标签。



