人物:莱布尼茨
莱布尼茨(Gottfried Wilhelm Leibniz,1646年7月1日-1716年11月14日),[1]出生于德国莱比锡,毕业于莱比锡大学,德国哲学家、数学家,被誉为“十七世纪的亚里士多德”。
莱布尼茨12岁时自学拉丁文,并着手学习希腊文。14岁时进入莱比锡大学念书,20岁时完成学业,专攻法律和一般大学课程。1666年他出版第一部有关于哲学方面的书籍,书名为《论组合术》(de arte combinatoria)。
人物生平

莱布尼茨1646年7月1日,戈特弗里德·威廉·莱布尼茨出生于神圣罗马帝国的莱比锡,祖父三代人均曾在萨克森政府供职,父亲是Friedrich Leibnütz,母亲是Catherina Schmuck。长大后,莱布尼茨名字的拼法才改成“Leibniz”,但是一般人习惯写成“Leibnitz”。晚年时期,他的签名通常写成“von Leibniz”,以示贵族身份。莱布尼茨死后,他的作品才公诸于世,作者名称通常是“Freiherr [Baron] G. W. von Leibniz.”,但没有人确定他是否确实有男爵的贵族头衔。
莱布尼茨的父亲是莱比锡大学的伦理学教授,在莱布尼茨6岁时去世,留下了一个私人的图书馆。[5]12岁时自学拉丁文,并着手学习希腊文。14岁时进入莱比锡大学念书,20岁时完成学业,专攻法律和一般大学课程。1666年他出版第一部有关于哲学方面的书籍,书名为《论组合术》(de arte combinatoria)。
工作经历
1666年莱布尼茨于Altdorf拿到博士学位后,拒绝了教职的聘任,并经由当时政治家Boineburg男爵的介绍,任职服务于美茵茨选帝侯大主教Johann Philipp von Schönborn的高等法庭。
1671年发表两篇论文《抽象运动的理论》(Theoria motus abstracti)及《新物理学假说》(Hypothesis physica nova),分别题献给巴黎的科学院和伦敦的皇家学会,在当时欧洲学术界增加了知名度。[6]
1672年莱布尼茨被Johann Philipp派至巴黎,以动摇路易十四对入侵荷兰及其它西欧日尔曼邻国的兴趣,并转投注精力于埃及。这项政治计划并没有成功,但莱布尼茨却进入了巴黎的知识圈,结识了马勒伯朗士和数学家惠更斯等人。这一时期的莱布尼茨特别研究数学,而且发明了微积分。
1672及1673年Boineburg和Johann Philipp却相继过世,迫使莱布尼茨最后于1676年离开巴黎而转任职服务于汉诺威的Johann Friedrich公爵。于上任时,顺道于海牙拜访斯宾诺莎,与其数天一同讨论哲学。之后莱布尼茨就到汉诺威管理图书馆,并担任公爵法律顾问。
1680至1685年间,担任哈茨山银矿矿采工程师。在这期间,莱布尼茨致力于风车设计,以抽取矿坑中的地下水。然而受限于技术问题和矿工传统观念的阻力,计划没有成功。
1685年起,再受继任的公爵Ernst August所托,转而开始做其Braunschweig-Lüneburg贵族族谱研究。这项计划一直到莱布尼茨去世前都没有完成。
1686年完成《形而上学论》(Discours de métaphysique)。
1689年为完成Braunschweig-Lüneburg族谱研究,游历于意大利。其时结识耶稣会派遣于中国的传教士,而开始对中国事物有更强烈的兴趣。
1695年于期刊发表《新系统》,进而使莱布尼茨哲学中,关于实体间与心物间之“预定和谐”理论,被广泛认识。
1700年莱布尼茨说服勃兰登堡选帝侯腓特烈三世于柏林成立科学院,并担任首任院长。
1704年完成《人类理智新论》。本文针对洛克的《人类理智论》,用对话的体裁,逐章节提出批评。然因洛克的突然过世,莱布尼茨不愿被落入欺负死者的口实,所以本书在莱布尼茨生前一直都没有出版。
1710年,出于对1705年过世的普鲁士王后Sophie Charlotte的感念,出版《神义论》(Essais de Théodicée)。
1714年于维也纳著写《单子论》(La Monadologie;标题为后人所加)及《建立于理性上之自然与恩惠的原理》。同年,汉诺威公爵Georg Ludwig继任为英国国王乔治一世,却拒绝将莱布尼茨带至伦敦,而将他疏远于汉诺威。
人物逝世
1716年11月14日莱布尼茨于汉诺威孤独地过世,除了他自己的秘书外,即使George Ludwig本人正巧在汉诺威,宫廷无其他人参加他的丧礼。直到去世前几个月,才写完一份关于中国人宗教思想的手稿:《论中国人的自然神学》。
主要成就
微积分

莱布尼茨现今在微积分领域使用的符号仍是莱布尼茨所提出的。在高等数学和数学分析领域,莱布尼茨判别法是用来判别交错级数的收敛性的。
莱布尼茨与牛顿谁先发明微积分的争论是数学界至今最大的公案。莱布尼茨于1684年发表第一篇微分论文,定义了微分概念,采用了微分符号dx,dy。1686年他又发表了积分论文,讨论了微分与积分,使用了积分符号∫。依据莱布尼茨的笔记本,1675年11月11日他便已完成一套完整的微分学。
然而1695年英国学者宣称:微积分的发明权属于牛顿;1699年又说:牛顿是微积分的“第一发明人”。1712年英国皇家学会成立了一个委员会调查此案,1713年初发布公告:“确认牛顿是微积分的第一发明人。”莱布尼茨直至去世后的几年都受到了冷遇。由于对牛顿的盲目崇拜,英国学者长期固守于牛顿的流数术,只用牛顿的流数符号,不屑采用莱布尼茨更优越的符号,以致英国的数学脱离了数学发展的时代潮流。
不过莱布尼茨对牛顿的评价非常的高,在1701年柏林宫廷的一次宴会上,普鲁士国王腓特烈询问莱布尼茨对牛顿的看法,莱布尼茨说道:“在从世界开始到牛顿生活的时代的全部数学中,牛顿的工作超过了一半”[7]。
牛顿在1687年出版的《自然哲学的数学原理》的第一版和第二版也写道:“十年前在我和最杰出的几何学家莱布尼茨的通信中,我表明我已经知道确定极大值和极小值的方法、作切线的方法以及类似的方法,但我在交换的信件中隐瞒了这方法,……这位最卓越的科学家在回信中写道,他也发现了一种同样的方法。他并诉述了他的方法,它与我的方法几乎没有什么不同,除了他的措词和符号而外”(但在第三版及以后再版时,这段话被删掉了)。因此,后来人们公认牛顿和莱布尼茨是各自独立地创建微积分的。
牛顿从物理学出发,运用集合方法研究微积分,其应用上更多地结合了运动学,造诣高于莱布尼茨。莱布尼茨则从几何问题出发,运用分析学方法引进微积分概念、得出运算法则,其数学的严密性与系统性是牛顿所不及的。
莱布尼茨认识到好的数学符号能节省思维劳动,运用符号的技巧是数学成功的关键之一。因此,他所创设的微积分符号远远优于牛顿的符号,这对微积分的发展有极大影响。1714至1716年间,莱布尼茨在去世前,起草了《微积分的历史和起源》一文(本文直到1846年才被发表),总结了自己创立微积分学的思路,说明了自己成就的独立性。
拓扑学
拓扑学最早称之“位相分析学”(analysis situs),是莱布尼茨1679年提出的,这是一门研究地形、地貌相类似的学科,当时主要研究的是出于数学分析的需要而产生的一些几何问题。关于莱布尼茨对拓扑学的贡献,尚存争论。Mates引用Jacob Freudenthal1954年一篇论文里的话说:
尽管莱布尼茨认为一列点在空间中的位置是由其间距离唯一决定的——当且仅当距离发生变化时点的位置发生相应的改变——他的仰慕者欧拉,在他著名的一篇论文(1736年发表,解决了柯尼斯堡七桥问题及其推广)中,却是在“拓扑变形时点的位置不发生变化”的意义下使用“几何位置”这个名词的。他误信了莱布尼茨是这个概念的创始者。……人们常常意识不到莱布尼茨是在完全不同的意义下使用这个名词的,因此被尊为数学的这个分支领域的奠基人并不恰当。
但平野秀秋持有不同看法,他引用本华·曼德博的话说:
在 莱布尼茨海量的科学成果中探索是发人深省的体验。除了微积分以及其他已经完成的研究之外,大量涉及内容广泛且极富前瞻性的研究对科学发展的推动力势不可 挡。在‘填充理论’上即有例子,……在发现莱布尼茨还曾经关注过几何度量的重要性之后,我对他的狂热更甚了。在“欧几里德普罗塔”中……,其使得欧几里德 公理更加严格,他陈述道,……‘对直线,我有数种不同的定义。直线是曲线的一种,而曲线的任何部分都是和整体相似的,因此直线也具有这种特性;这不仅适用 于曲线,而且适用于集合。’这个论断今天已经可以被证明。
因而分形几何(由本华·曼德博发扬光大)理论在莱布尼茨的自相似性思想和连续性原理中寻求支持:大自然没有跳跃(拉 丁语“natura non facit saltus”,英语"nature does not make jumps")。当莱布尼茨在他的形而上学著作中写道,“直线是曲线的一种,其任何部分都是和整体类似的”,他实际上提前两个世纪预言了拓扑学的诞生。至 于“填充理论”,莱布尼茨对他的朋友Des Bosses说,“你想象一个圆,然后用三个全等的最大半径的圆填满它,后来的三个小圆又可以以同样的过程被更小的圆填充”。这个过程可以无限地继续下 去,并由此生发出了自相似性的思想。莱布尼茨对于欧氏公理的改进亦包含同样的概念。
符号思维
莱布尼茨有个显著的信仰,大量的人类推理可以被归约为某类运算,而这种运算可以解决看法上的差异:
"精炼我们的推理的唯一方式是使它们同数学一样切实,这样我们能一眼就找出我们的错误,并且在人们有争议的时候,我们可以简单的说: 让我们计算[calculemus],而无须进一步的忙乱,就能看出谁是正确的。" (发现的艺术 1685, 51)
莱布尼茨的演算推论器,很能让人想起符号逻辑,可以被看作使这种计算成为可行的一种方式。莱布尼茨写的备忘录(帕金森1966年翻译了它们)可以被看作是对符号逻辑的探索--所以他的演算--上路了。但是 Gerhard 和 Couturat 没有出版这些著作,直到现代形式逻辑在 1880 年代于 Frege 的概念文字 和 Charles Peirce 及他的学生的著作中形成,所以就更在乔治·布尔和德·摩根在 1847 开创这种逻辑之后了。
单子论

除了是一位出众的天才数学家之外,莱布尼茨亦是欧陆理性主义哲学的高峰。承断了西方哲学传统的思想,他认为世界,因其确定(换句话说,有关世界的知识是客观普遍和必然的)之故,必然是由自足的实体所构成。所谓的自足,是不依他物存在和不依他物而被认知。莱布尼茨的前辈斯宾诺莎以为实体只有一个,就是神/自然。莱布尼茨对此不敢苟同,原因之一是斯氏的泛神观和圣经的神学有明显冲突,其次,是因为斯氏的理论没有能够解决由笛卡儿以降的二元论,令世界出现了断层(他虽然强调世界为一,但没有说明这一个看来是二元对立的世界的一统是如何可能)。
莱布尼茨以为实体是多的,是无限多的。跟随亚里士多德的实体观,他以为实体是一命题的主语。在一个命题S是P中,S就是实体。因为实体是自足的,则它要包含所有可能的谓语,即是“...是P”。由此,我们可以推出,实体有四个特征:不可分割性、封闭性、统有性和道德性。
不可分割性是指,任何有广延的东西,即有长度的东西,都可以被分割。被分割了的东西分别包含了自己的全部可能性,并且自足,则有广延的东西的内容,即可能性要依附于他的部分的可能性。如此类推,则只要有广延性,就不自足,而要依他物而被知(对莱布尼茨来说,真正的知识就是要穷一物的可能性),就不是实体。故实体不可分割,是一没有广延的东西,在莱布尼茨的晚年著作中(Monadology),他称之为单子(Monad),单子的性质就是思(thought)。这广延的世界就是由无限多的单子构成。
封闭性是说每一单子必然是自足的,不依他而存在,而又包含了自己的全部可能性。则一单子不可能和另一单子有交互作用(interaction)。若一单子作用于另一单子,则后一单子有一可能性没有包括在该单子之内,即该单子没能自足的包含自己的全部内容,而要依附于他物。因为实体的定义,这是不可能的。故莱布尼茨说:“单子之间没有窗户。”
统有性是指每一单子都必然以某种角度(perspective)包括了全世界。因为世界是紧密的由因果所构成,故A作用于B,其实不单单是作用于B,而是全世界。如果说一单子的内容包括自身的全部可能,则每一单子均以该单子自身为中心指向全世界。而这个世界是一的,不等于说所有单子都是一样的,因为同一世界可以不同的角度来认知,而不失为一一统的世界。
最后,单子的道德性则较复杂。这个特性的提出是基于两个理由,一、是世界的一统性(unity),二、是世界的确定性。对于前者,所有的单子都包含全世界,但各以自己的角度,世界的一统性是不是假的呢?如果我们要说一统,可以如何说起呢?对于后者,世界是由单子构成,单子只是其可能性的集合,世界亦只是一可能。那我们是不是不可能有一种不仅仅是可能,而是必然的知识呢?我们可以在什么意义下说有关世界的知识是真的、确定的呢?莱布尼茨将之归功于一神,世界的创造者。从一个方面说,神在创造之前,没有已成的材料,故没有既成的有限处境,则创造是一纯意志的创造,神是单凭其至善而创造这一个世界的。
故此,如莱布尼茨的名言,这一个确切成就了的世界是“众多可能的世界之中最好的一个。”这乎合了莱布尼茨的信仰要求。另一方面,要确定的了解一事物,则要了解其原因。要理解这一个原因,又要追索该原因的原因。如此类推,则世界的确定性知识不可能是一世界之内的动因(efficient cause),而是一超越的形上因(metaphysical cause)。
莱布尼茨称这个理论上必要设置的形上因为神。故,这一个世界之所以是如此,就是因为这是最好的,是至善的可能世界。人,要完全理解这神的至善意志,是不可能的,但可朝这一个方向迈进,因为人的心灵作一特殊的单子,是有记忆的,可以基于过去,畴划自己的未来,这是人类分享的神性,即道德的可能性。人可以透过开放可能性,了解这个神创造的世界,而了解如何成为一个道德的人。
这一种世界的道德观,可以被视为康德的先驱,分别在于莱布尼茨独断的提出了神为道德的完满,把可能性说成了是在神的目光之下的实在,而没有真正的将世界的可能性看作为可能性。而且莱布尼茨对天赋观念(innate idea)的批评,正是黑格尔对康德的批评,在这个意义上说,康德一方面是被休谟(Hume)从莱布尼茨的独断梦中唤醒,可是同时亦到由洛克(Locke)起的哲学病变--对理性界限的审查--所污染。在这一方面,莱布尼茨却比康德走前了一步。
形式逻辑
莱布尼茨是在亚里士多德和1847年乔治·布尔和德·摩根分别出版开创现代形式逻辑的著作之间最重要的逻辑学家。莱布尼茨阐明了合取、析取、否定、同一、集合包含和空集的首要性质。莱布尼茨的逻辑原理和他的整个哲学可被归约为两点:
所有的我们的观念(概念)都是由非常小数目的简单观念复合而成,它们形成了人类思维的字母。
复杂的观念来自这些简单的观念,是由它们通过模拟算术运算的统一的和对称的组合。
人物评价
莱布尼茨不仅在西方哲学史上享有崇高的地位,且在西方逻辑史上也享有崇高的地位。(贵州大学学报评)
他是现代逻辑的奠基者,陆理性主义的代表人物之一,关注最多的还是理性论证。(自然辩证法通讯评)
轶事典故
莱布尼茨与中国文化
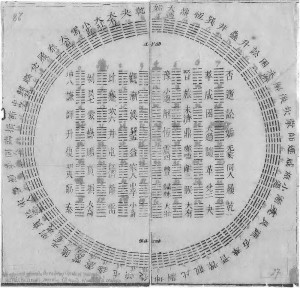
1701年白晋给莱布尼茨的周易图莱布尼茨是最早接触中华文化的欧洲人之一,曾经从一些曾经前往中国传教的教士那里接触到中国文化,之前应该从马可·波罗引起的东方热留下的影响中也了解过中国文化。法国汉学大师若阿基姆·布韦(Joachim Bouvet,汉名白晋,1662-1732年)向莱布尼茨介绍了《周易》和八卦的系统。在莱布尼茨眼中,“阴”与“阳”基本上就是他的二进制的中国版。他曾断言:“二进制乃是具有世界普遍性的、最完美的逻辑语言”。今天在德国图林根,著名的郭塔王宫图书馆(Schlossbibliothek zu Gotha)内仍保存一份莱氏的手稿,标题写着“1与0,一切数字的神奇渊源。”
其手稿标题全文是:《1与0,一切数字的神奇渊源。……这是造物的秘密美妙的典范,因为,一切无非都来自上帝。》,而且莱布尼茨自己写给若阿基姆·布韦的信中莱布尼茨写到的是:“第一天的伊始是1,也就是上帝。第二天的伊始是2,……到了第七天,一切都有了。所以,这最后的一天也是完美的。因为,此时世间的一切都已经被创造出来了。因此它被写作‘7’,也就是‘111’(二进制中的111等于十进制的7),而且不包含0。只有当我们仅仅用0和1来表达这个数字时,才能理解,为什么第七天才完美,为什么7是神圣的数字。特别值得注意的是它(第七天)的特征(写作二进制的111)与三位一体的关联。”
郭书春在《古代世界数学泰斗刘徽》一书461页中称:“中国有所谓《周易》创造了二进制的说法,至于莱布尼兹受《周易》八卦的影响创造二进制并用于计算机的神话,更是广为流传。事实是,莱布尼兹先发明了二进制,后来才看到传教士带回的宋代学者重新编排的《周易》八卦,并发现八卦可以用他的二进制来解释。”以此为由,认为并不是莱布尼茨看到阴阳八卦才发明二进制。梁宗巨著《数学历史典故》(1995年出版)一书14~18页对这一历史公案亦有此说。
胡阳、李长铎在《莱布尼茨发明二进制前没有见过先天图吗——对欧洲现存17世纪中西交流文献的考证》通过对欧洲现存17世纪中西交流文献的研究考证,否定了莱布尼茨在发明二进制以后才见到先天图的说法。先天图在莱布尼茨发明二进制之前,已被斯比塞尔称之为二进制。
有关莱布尼茨二进制与中国古代典籍《易经》关系问题的讨论涉及如何看待近代中西文化的各自特质以及它们之间的相互作用问题。虽然二进制只是一种算术记数法和计数法,但它实际上是特定文化(包括数学、语言、符号、逻辑和哲学等)的产物。现有观点中的一个明显不足是把与二进制相关的概念、理论(原理、符号等)的形成与发展看作是单因素的、一次性完成的结果,又把二进制与《易经》哲学和卦图的相互作用关系看作是“全或无”的关系,从而忽视了概念、理论的形成和变化过程,也容易导致两种极端的判断。
因此,立足于近代中西文化交流的大背景,从概念与认知分析入手,能够把莱布尼茨二进制思想的形成过程置于近代中西文化交流所编织的概念网络系统之中,进而梳理出莱布尼茨在秉承西方近代数学概念的同时,如何通过获取和吸纳《易经》概念资源而实现概念的创造性转换的脉络。我们看到,除了莱布尼茨个人的独创性的伟大贡献外,近代意义上的二进制实际上是“中西合璧”的产物。





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本