1009练习赛
反思
这次1008练习赛考的并不好。
T1倒是很快就切了,因为以前做过一模一样的。
T2的话,被可怕的数据范围吓到了,花了太多时间在T2上。
最开始我也分析了一会儿复杂度,似乎感觉这道题数据不可能像想象中的那么可怕,可是自己说不清楚为什么。。。最终只能写了个暴力并查集。
以后要动笔仔细分析清楚,不要怕暴力,说不定能有很多分呢。
T3,没有推出第一个结论gcd(a^x-1,a^y-1)==a^(gcd(x,y))-1,而是直接去想各种容斥,却又想不出来。
遇到数学式子,要尝试先化简成自己好做的形式,不要操之过急。
然后呢,听评讲的时候,看到求gcd==d的个数时,我能想起以前XYM讲CF时讲过,我自己还写过,可一点都回忆不起来。还有那个欧拉函数,我也是忘得差不多了。
数论急需复习复习复习。
T4,思路太混乱,线段树合并不够熟悉(应该说是完全不太会)。主席树也想不出来,就写不了了。
T1 话中有话 NKOJ8651
有些词是多义词。这就导致同一句话可能有多种解读,即话中有话。 何老板给你一个字符串A,同时给你一个单词B。单词B有两种不同的含义。 何老板想知道,字符串有多少种不同的解读? 例如: A=xixixixi B=xixi, 设"xixi"除了默认的含义外,还有另一种含义“嘻嘻” "xixixi"的解读有:xixixi,嘻嘻xi,xi嘻嘻,共三种 数据范围: 0<=|B|<=|A|<=100000
这道题很明显需要在A中匹配B,所以我们用kmp找到所有可以匹配的位置。
找到之后呢,用dp递推即可。
前$i$位可以表示的含义数量记为$f[i]$
1. $f[i] = f[i-1]$
2. 如果第$i$位可以匹配,$f[i] += f[i-lenB]$

#include<bits/stdc++.h> using namespace std; #define re register int #define int long long const int N=1e5+5,mo=1e9+7; int f[N], kmp[N], fail[N]; char A[N], B[N]; signed main() { scanf("%s%s",&A[1],&B[1]); int l1=strlen(A+1),l2=strlen(B+1); for(re i=2,j=0;i<=l2;++i) { while(j&&B[i]!=B[j+1])j=fail[j]; if(B[i]==B[j+1])j++; fail[i]=j; } for(re i=1,j=0;i<=l1;++i) { while(j&&A[i]!=B[j+1])j=fail[j]; if(A[i]==B[j+1])j++; kmp[i]=j; } f[0]=1; for(re i=1;i<=l1;++i) { f[i]=f[i-1]; if(kmp[i]==l2)f[i]+=f[i-l2]; f[i]%=mo; } printf("%lld\n",f[l1]); return 0; }
T2 岛中有桥 NKOJ8644
n个岛屿,已知有m对岛屿不可直接相互建桥. 问最少能形成多少个连通块(连通块中岛屿与岛屿可以相互到达). 以及每个连通块中的岛屿个数。 数据范围: 1<=n<=200000, 1<=m<=min(n*(n-1)/2,200000)
这道题很神奇,暴力是能过的,因为一些神奇的性质,但kzsn没怎么弄清楚...
值得一提的是,我大数据过了,但一个n<=1000的小数据WA了。
所以以后考试有时间的话,一定要按照数据梯度来写一写那些小暴力,这样可以保证小数据能过!切记!

#include<bits/stdc++.h> using namespace std; #define re register int const int N=1e6+6; int n,m,in[N],fa[N],sz[N],a[N],cnt,ans[N]; inline int getf(int x){return fa[x]==x?x:fa[x]=getf(fa[x]);} inline bool cmp(int x,int y){return in[x]<in[y];} map<int,bool>mp[N]; signed main() { scanf("%d%d",&n,&m); while(m--) { int x, y; scanf("%d%d",&x,&y); if(1<=x&&x<=n&&1<=y&&y<=n&&x!=y) { mp[x][y]=1;mp[y][x]=1; in[x]++;in[y]++; } } for(re i=1;i<=n;++i)a[i]=fa[i]=i,sz[i]=1; if(n<=1000) { for(re i=1;i<=n;++i) { int x=getf(i); for(re j=1;j<=n;++j) { if(!mp[i][j] && getf(j)!=x) { int y=getf(j); fa[y]=x; sz[x]+=sz[y]; } } } for(re i=1;i<=n;++i)if(getf(i)==i)ans[++cnt]=sz[i]; if(!cnt)return printf("0"),0; printf("%d\n",cnt); sort(ans+1,ans+1+cnt); for(re i=1;i<=cnt;++i) { printf("%d",ans[i]); if(i!=cnt)printf(" "); } return 0; } sort(a+1,a+1+n,cmp); for(re i=1;i<=n;++i) { int x=a[i]; if(fa[x]==x) { for(re j=1;j<=n;++j) { if(!mp[x][j]&&!mp[j][x]&&getf(j)!=x) { sz[x]+=sz[getf(j)]; fa[getf(j)]=x; } } } } for(re i=1;i<=n;++i)if(getf(i)==i)ans[++cnt]=sz[i]; if(!cnt)return printf("0"),0; printf("%d\n",cnt); sort(ans+1,ans+1+cnt); for(re i=1;i<=cnt;++i) { printf("%d",ans[i]); if(i!=cnt)printf(" "); } return 0; }
T3 数中有学 NKOJ8631
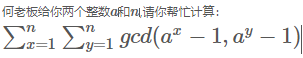

首先第一步,我们需要将给出的式子化简成我们好做的形式:
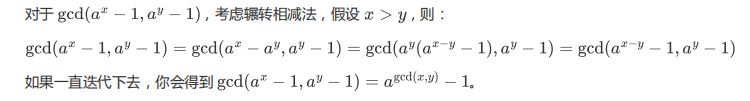
得到这里,我们继续化简

于是,这道题便转化为了求互质的个数。
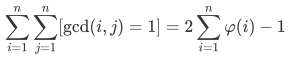
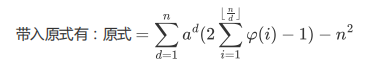
我们可以预处理出欧拉函数的前缀和,然后
#include<bits/stdc++.h> using namespace std; #define re register int #define LL long long const int mo=1e9+7; LL fly[1000006]; void init() { const int MXN=1e6; for(re i=0;i<=MXN;++i)fly[i]=i; for(re i=2;i<=MXN;++i) if(fly[i]==i){ for(re j=i;j<=MXN;j+=i) fly[j]=fly[j]/i*(i-1); } fly[0]=-1; for(re i=1;i<=MXN;++i) fly[i]=(fly[i-1]+fly[i]*2)%mo; } inline LL ksm(LL x,int y) { LL ret=1; while(y) { if(y&1)ret=ret*x%mo; y>>=1; x=x*x%mo; } return ret; } signed main() { init(); int T,a,n; scanf("%d",&T); while(T--) { scanf("%d%d",&a,&n); LL ret=0,iv=ksm(a-1,mo-2); for(re l=1,r=1;l<=n;l=r+1) { int t=n/l;r=min(n,n/t); ret+=((ksm(a,r+1)-ksm(a,l))%mo+mo)%mo*iv%mo*fly[t]%mo; } ret=((ret-1ll*n*n%mo)%mo+mo)%mo; printf("%lld\n",ret); } return 0; }
这道题还可以莫比乌斯反演,以后一定要学会!!!
T4 山中有牛 NKOJ8632
n个村庄形成一棵树,其中1号节点为根。
每个村庄都有海拔高度hi,离村庄1越近的村庄海拔越高。
山里的居民大都会样耗牛,不同的耗牛能适应的海拔不同。
今天有m头牛出生,已知每头牛出生的村庄以及它能适应的海拔范围[a,b],求它能在多少个村庄内活动。
数据范围:
1<=n,m<=100000,1<=hi<=10^9,1<=a<b<=10^9。
对于每头牛,先找到它能生存的最高的点(也就是该村庄的祖先中海拔小于等于b的最接近1号村庄的村庄),村庄t。
然后这道题便转化成了在t的子树里,有多少点的权值大于等于a,可以用主席树,也可以线段树合并!
注意需要离散化!

#include<bits/stdc++.h> using namespace std; #define re register int const int N=5e5+5; int root[N], seg; struct segment{int a, b, v, ls, rs;}tr[N<<3]; inline int build(int l, int r) { int p=++seg; tr[p].a=l;tr[p].b=r; if(l!=r) { int mid=(l+r)>>1; tr[p].ls=build(l,mid); tr[p].rs=build(mid+1,r); } return p; } inline int merge(int pre, int t) { int p=++seg; tr[p]=tr[pre];tr[p].v=tr[pre].v+1; if(tr[p].a<tr[p].b) { int mid=(tr[p].a+tr[p].b)>>1; if(t<=mid)tr[p].ls=merge(tr[pre].ls,t); else tr[p].rs=merge(tr[pre].rs,t); } return p; } int fa[N][25],in[N],ou[N],tot,h[N],lst[N]; int tt,las[N],ed[N],nt[N]; inline void add(int x,int y){ed[++tt]=y;nt[tt]=las[x];las[x]=tt;} inline void dfs(int x,int pre) { fa[x][0]=pre; for(re i=1;i<=20;++i)fa[x][i]=fa[fa[x][i-1]][i-1]; in[x]=++tot; root[in[x]]=merge(root[in[x]-1],h[x]); for(re i=las[x];i;i=nt[i]) { int v=ed[i]; if(v!=pre)dfs(v,x); } ou[x]=tot; } inline int query(int p1, int p2, int k) { if(k<=tr[p1].a)return tr[p2].v-tr[p1].v; int mid=(tr[p1].a+tr[p1].b)>>1,ret=0; if(k<=mid)ret+=query(tr[p1].ls,tr[p2].ls,k); ret+=query(tr[p1].rs,tr[p2].rs,k); return ret; } signed main() { int n; scanf("%d",&n); for(re i=1;i<n;++i) { int x,y; scanf("%d%d",&x,&y); add(x,y); add(y,x); } for(re i=1;i<=n;++i)scanf("%d",&h[i]),lst[i]=h[i]; sort(lst+1,lst+1+n); int cnt=unique(lst+1,lst+1+n)-lst-1; for(re i=1;i<=n;++i)h[i]=lower_bound(lst+1,lst+1+cnt,h[i])-lst; root[0]=build(1,cnt); dfs(1,0); int m; scanf("%d",&m); while(m--) { int k,a,b; scanf("%d%d%d",&k,&a,&b); if(!(a<=lst[h[k]]&&lst[h[k]]<=b)){puts("0");continue;} for(re i=20;~i;--i)if(fa[k][i]&&lst[h[fa[k][i]]]<=b)k=fa[k][i]; a=lower_bound(lst+1,lst+1+cnt,a)-lst; printf("%d\n",query(root[in[k]-1],root[ou[k]],a)); } }


