0717跳马

T1 跳马

简要题意：

一个n*m的棋盘，“马”棋子要从坐标(0,0)，跳到(n,m)。

每次跳的方法有两种：即横坐标跳1、纵坐标跳2，或者横坐标跳2，纵坐标跳1。

马的每一次跳跃，横纵坐标都要离目标更近。

问有多少中跳法。方案书对10⁹+7取模。

分析：

我们设横跳a次，纵跳b次。

那么很容易列出一个方程：

2*a+b=m； 2*b+a=n

解出来 a=(2*m-n)/3； b=(2*n-m)/3

既然知道了横纵跳各多少次，那么C(a，a+b)即是我们的答案了。

易错点：

我们解出的a,b是需要判断一下的！

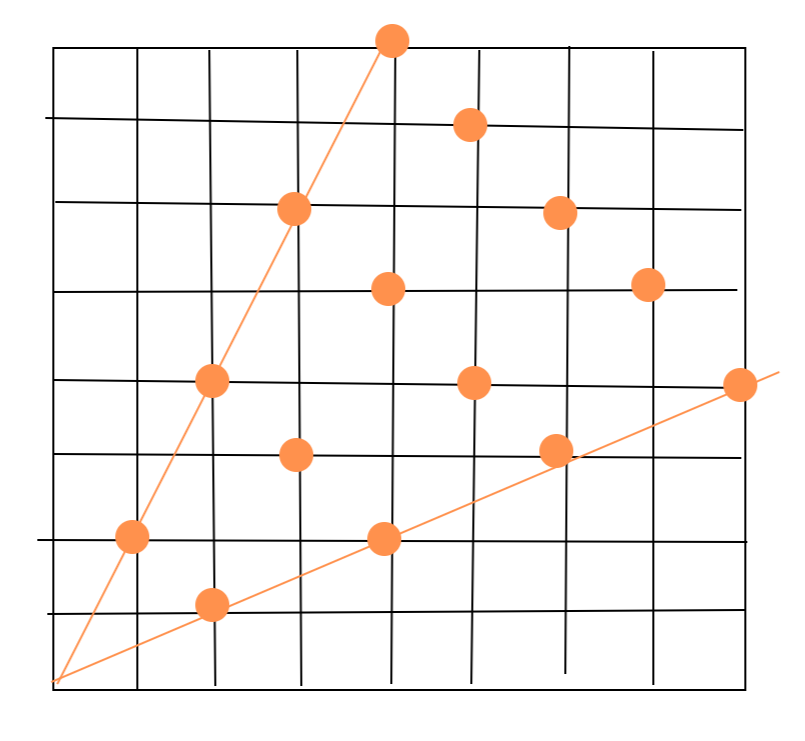
根据上图，我们很容易知道几种特判

1.(n+m)%3 != 0

2. 2*m<n || 2*n<m

3. a<0 || b<0

这三种情况下，直接输出“0”即可

kzsn当时只判断了a,b是不是都是正整数，然后痛失30分！

 

#include<bits/stdc++.h>
using namespace std;
#define LL unsigned long long
const LL mo=1e9+7;
inline LL ksm(LL x,LL y)
{
    LL ret=1ll;
    while(y)
    {
        if(y&1)ret=ret*x%mo;
        x=x*x%mo;
        y>>=1;
    }
    return ret;
}
inline LL getc(const LL x, const LL y)
{
    LL ret=1ll, tmp=y-x;
    for(register LL i=y;i;--i)
    {
        ret=ret*i%mo;
        if(i<=x)ret=ret*ksm(i,mo-2)%mo;
        if(i<=tmp)ret=ret*ksm(i,mo-2)%mo;
    }
    return ret;
}
signed main()
{
    int n,m;scanf("%d%d",&n,&m);
    if((n+m)%3!=0)return puts("0"),0;
    if(n*2<m||2*m<n)return puts("0"),0;
    LL a=1ll*(2*n-m)/3,b=1ll*(2*m-n)/3;
    if(a<0 || b<0)return puts("0"),0;
    printf("%llu",getc(a,a+b));
    return 0;
}

 

“结合图形要牢记，莫把特判当儿戏” ----《kzsn语录》kzsn