热身训练1 Sequence

http://acm.hdu.edu.cn/showproblem.php?pid=6

分析：

这道题，全都是1e9，所以我们很容易想到“矩阵快速幂”。

假如说我们没有后面那个“向下取整”的东西，而将他看作一个常熟C

我们可以很轻松的得到矩阵幂的式子

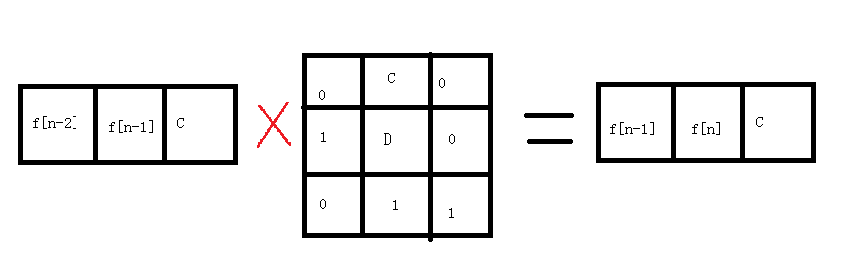
然后呢，那个常熟C却会随着i变化

我们只需要整除分块，分别进行矩阵幂，这道题就解决了

#include<bits/stdc++.h>
using namespace std;
#define re register int
#define LL long long
#define int long long
const int mo = 1e9+7;
typedef int arr[10][10];
arr A, ans;
void modi(arr y, arr x)
{
    arr z; memset(z, 0, sizeof(z));
    for(re i=1;i<=3;++i)
    {
        for(re j=1;j<=3;++j)
        {
            for(re k=1;k<=3;++k)
            {
                z[i][j] = (z[i][j] + y[i][k]*x[k][j] % mo) % mo;
            }
        }
    }
    memcpy(y, z, sizeof(z));
}
int a, b, c, d, p, n, q;
void Montgomery(int pp)
{
    ans[1][3] = q % mo;
    memset(A, 0, sizeof(A));
    A[1][2]=c%mo; A[2][2]=d%mo; A[2][1]=A[3][2]=A[3][3]=1ll;
    while(pp)
    {
        if(pp&1) modi(ans, A);
        pp>>=1;
        modi(A,A);
    }
}
inline void work()
{
    scanf("%lld%lld%lld%lld%lld%lld",&a,&b,&c,&d,&p,&n);
    if(n == 1) printf("%lld\n", a);
    else if(n == 2) printf("%lld\n", b);
    else
    {
        memset(ans, 0, sizeof(ans));
        ans[1][1]=a;
        ans[1][2]=b;
        for(re i=3;i<=n;)
        {
            q = p/i;
            int nt;
            if(q == 0) nt=n; else nt = min(n, p/q);
            Montgomery(nt-i+1);
            i=nt+1;
        }
        printf("%lld\n", ans[1][2] % mo);    
    }
    
}
signed main()
{
    int T;scanf("%lld",&T);
    while(T--) work();
}

made by kzsn

“向着风拥抱彩虹，勇敢的向前走”

“黎明的那道光，会越过黑暗”

“打破一切恐惧我能，找到答案” ----《你的答案》阿冗