后缀数组

一些废话

• SA 可以做的，SAM 也一定可以做 （所以学什么 SA 啊）

• 直到我遇到了这个题：P4051 [JSOI2007]字符加密

• 然后 SAM 就死了，大概 SAM 遇到字符集大的问题确实是束手无策，因为空间和时间上确实会被 SA 碾压

• 但是我是觉得应该没有出题人无聊到卡这种东西吧

SA

构造

P3809 【模板】后缀排序

• 我们称一个后缀子串的位置为它的首字母的下标，这里的下标从 1 开始

• 设 \(sa[i]\) 表示字典序排名为 \(i\) 的后缀子串的位置

• 那么一个暴力排序方法就是 \(n^2\log n\)

• 考虑用倍增来优化，偷了一张图：

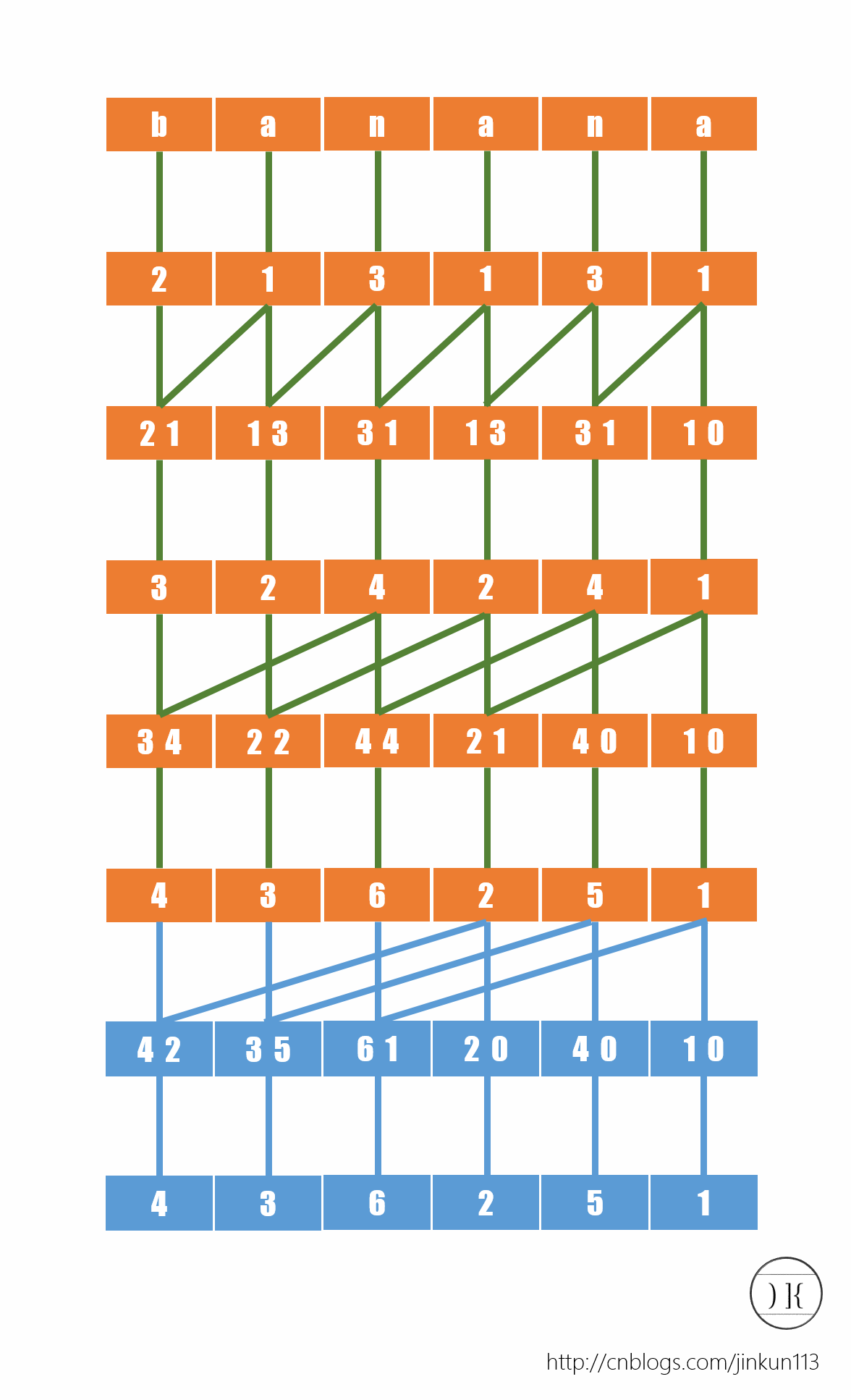
• 因为每一次的关键字只有 2 个，所以考虑基数排序优化

• 最终的复杂度就是 \(O(n\log n)\)

int c[N],m=300,x[N],y[N],sa[N];
inline void SA(){
    FOR(i,1,n) ++c[x[i]=S[i]];
    FOR(i,2,m) c[i]+=c[i-1];
    ROF(i,n,1) sa[c[x[i]]--]=i;
    for(int k=1;k<=n;k<<=1) {
        int num=0;
        FOR(i,n-k+1,n) y[++num]=i;
        FOR(i,1,n) if(sa[i]>k) y[++num]=sa[i]-k;
        FOR(i,1,m) c[i]=0;
        FOR(i,1,n) ++c[x[i]];
        FOR(i,2,m) c[i]+=c[i-1];
        ROF(i,n,1) sa[c[x[y[i]]]--]=y[i],y[i]=0;
        swap(x,y);
        x[sa[1]]=1;num=1;
        FOR(i,2,n) {
            x[sa[i]]=(y[sa[i]]==y[sa[i-1]] && y[sa[i]+k]==y[sa[i-1]+k])?num:++num;
        }
        if(num==n) break ;
        m=num;
    }
}

• 然后 P4051 [JSOI2007]字符加密 这个题就可以直接过了