[SDOI2013] 直径
题目描述
小Q最近学习了一些图论知识。根据课本，有如下定义。树：无回路且连通的无向图，每条边都有正整数的权值来表示其长度。如果一棵树有N个节点，可以证明其有且仅有N-1 条边。路径：一棵树上，任意两个节点之间最多有一条简单路径。我们用 dis(a,b)表示点a和点b的路径上各边长度之和。称dis(a,b)为a、b两个节点间的距离。
直径：一棵树上，最长的路径为树的直径。树的直径可能不是唯一的。
现在小Q想知道，对于给定的一棵树，其直径的长度是多少，以及有多少条边满足所有的直径都经过该边。
输入输出格式
输入格式：
第一行包含一个整数N，表示节点数。 接下来N-1行，每行三个整数a, b, c ，表示点 a和点b之间有一条长度为c的无向边。
输出格式：
共两行。第一行一个整数，表示直径的长度。第二行一个整数，表示被所有直径经过的边的数量。
输入输出样例
输入样例#1： 复制
8
0 1 1
1 2 2
2 3 3
3 4 4
3 7 4
2 6 3
1 8 1
输出样例#1： 复制
10
1
说明
【样例说明】 直径共有两条，3 到2的路径和3到6的路径。这两条直径都经过边(3, 1)和边(1, 4)。
对于100%的测试数据：2<=N<=200000，所有点的编号都在1..N的范围内，边的权值<=10^9。
Soultion
本题一看就是树的直径（题目都说了），它要求所有直径都经过的边的数量。
先看样例的图，把直径给标出来。
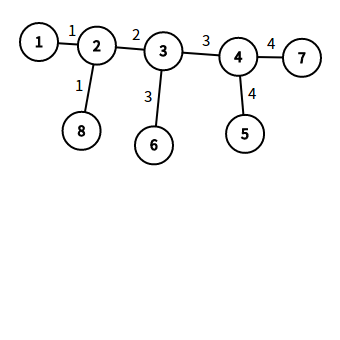
直径是1,2,3,4,7，直径长度为10，我们枚举直径上的点，只要验证是否存在一个长度，等于之前的长度就行啦。我们枚举到1，发现8可以替换0，所以8,2,3,47形成新的直径，显然1,2之间这条边不可能是重合的边，就这样推过去，可以发现只有中间的边是重合的边，但是我们需要判断当前这个点是往左走，还是往右走，例如8这个点，显然走往3，不会往1走，6是往4走，5是往3走。
代码如下：
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long lol;
struct node
{
lol to,next,w;
}a[500100];
lol len,last[500010],fa[501010],vis[501001],ans[501010],d[501010],l,r;
lol rr,ll;
void add(lol a1,lol a2,lol a3)
{
a[++len].to=a2;
a[len].w=a3;
a[len].next=last[a1];
last[a1]=len;
}
void dfs(lol x,lol father)
{
for(lol i=last[x];i;i=a[i].next)
{
lol to=a[i].to;
if(to==father||vis[to]) continue;
fa[to]=x;
d[to]=d[x]+a[i].w;
dfs(to,x);
}
}
void dfs1(lol x,lol father,lol id)
{
for(lol i=last[x];i;i=a[i].next)
{
lol to=a[i].to;
if(to==father||vis[to]) continue;
d[to]=d[x]+a[i].w;
if(d[to]==ans[id]||d[to]==ans[r]-ans[id])
rr=id;
dfs1(to,x,id);
}
}
void dfs2(lol x,lol father,lol id)
{
for(lol i=last[x];i;i=a[i].next)
{
lol to=a[i].to;
if(to==father||vis[to]) continue;
d[to]=d[x]+a[i].w;
if(d[to]==ans[id]||d[to]==ans[r]-ans[id])
if(!ll)
ll=id;
dfs2(to,x,id);
}
}
int main()
{
lol n,x,y,z;
cin>>n;
for(lol i=1;i<n;i++)
{
scanf("%lld%lld%lld",&x,&y,&z);
add(x,y,z);add(y,x,z);
}
dfs(1,0);
for(lol i=1;i<=n;i++) if(d[i]>d[l]) l=i;
memset(fa,0,sizeof(fa));memset(d,0,sizeof(d));
dfs(l,0);
for(lol i=1;i<=n;i++) if(d[i]>d[r]) r=i;
for(lol i=r;i;i=fa[i]) vis[i]=1,ans[i]=d[i];
cout<<d[r]<<endl;
memset(d,0,sizeof(d));
for(lol i=fa[r];fa[i]!=0;i=fa[i])
{
if(ans[i]*2>ans[r])
dfs1(i,0,i);
else
dfs2(i,0,i);
}
lol pp=0,p=0;
// cout<<ll<<' '<<rr<<endl;
for(lol i=r;fa[i];i=fa[i])
p++;
if(ll==0)
{
for(int i=rr;fa[i]!=0;i=fa[i])
pp++;
cout<<pp<<endl;
}
else if(rr==0)
{
for(int i=r;i!=ll;i=fa[i])
pp++;
cout<<pp;
}
else
{
for(int i=rr;i!=ll;i=fa[i])
pp++;
cout<<pp<<endl;
}
}