[模板] 严格次小生成树
题目描述
小C最近学了很多最小生成树的算法,Prim算法、Kurskal算法、消圈算法等等。正当小C洋洋得意之时,小P又来泼小C冷水了。小P说,让小C求出一个无向图的次小生成树,而且这个次小生成树还得是严格次小的,也就是说:如果最小生成树选择的边集是EM,严格次小生成树选择的边集是ES,那么需要满足:(value(e)表示边e的权值) $$\sum_{e∈EM}value(e)<\sum_{e∈ES}value(e)$$ 这下小 C 蒙了,他找到了你,希望你帮他解决这个问题。输入输出格式
输入格式:
第一行包含两个整数N 和M,表示无向图的点数与边数。 接下来 M行,每行 3个数x y z 表示,点 x 和点y之间有一条边,边的权值为z。
输出格式:
包含一行,仅一个数,表示严格次小生成树的边权和。(数据保证必定存在严格次小生成树)
输入输出样例
输入样例#1: 复制
5 6
1 2 1
1 3 2
2 4 3
3 5 4
3 4 3
4 5 6
输出样例#1: 复制
11
说明
数据中无向图无自环; 50% 的数据N≤2 000 M≤3 000; 80% 的数据N≤50 000, M≤100 000; 100% 的数据N≤100 000 M≤300 000 ,边权值非负且不超过 10^9 。
Solution
首先,我们得知道最小生成树和次小生成树只差一条边,我不会证明,想学的可以去网上找。严格次小生成树大致思路就是Kruskal+倍增LCA。
我们先用KrusKal求出最小生成树,标记一下哪些边用过,哪些边没用过,
我们肯定是用没用过的边去替换用过的边。
我们先看样例最小生成树的图片。
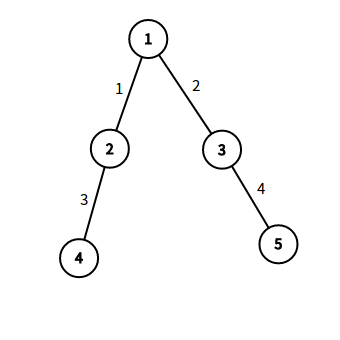
接下来我们枚举每一条不在最小生成树的边,枚举第一条,如图:
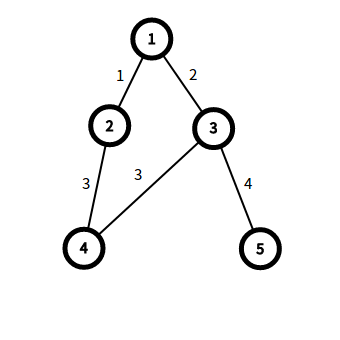
我们可以发现1,2,3,4成为了一个环,删掉任意一个环上的边都能形成生成树,我们容易得到新加入的这条边肯定是环上的最大值,(不然之前求的就不是最小生成树了)。我们只需换掉环上的最大的那条边就行了,但它要求严格次小,所以换的那条边不能等于当前这条边,所以我们还需维护一个严格次大值。那么我们怎么求解路径最大值和次大值呢?用倍增LCA维护一个最大值和次大值,就可以求解了。代码如下:
// luogu-judger-enable-o2
#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cstring>
using namespace std;
typedef long long ll;
ll last[100010],fa[201010],len,ans,dep[201010],f[201001][20],n,m;
ll mx1[201000][20],mx2[201000][20],vis[301000],pai[10],anss=100000000;
struct node
{
ll to,next,w;
}a[501010];
struct kzj
{
ll x,y,z;
bool operator< (const kzj &c) const{return c.z>z;}
}ff[301010];
void add(ll a1,ll a2,ll a3)
{
a[++len].to=a2;
a[len].w=a3;
a[len].next=last[a1];
last[a1]=len;
}
ll find(ll x)
{
if(x==fa[x]) return x;
return fa[x]=find(fa[x]);
}
void dfs(ll x,ll father)
{
for(ll i=last[x];i;i=a[i].next)
{
ll to=a[i].to;
if(to==father) continue;
dep[to]=dep[x]+1;
f[to][0]=x;
mx1[to][0]=a[i].w;
dfs(to,x);
}
}
bool cmp(ll a1,ll a2){return a1>a2;}
void zuxian()
{
for(ll j=1;j<=19;j++)
for(ll i=1;i<=n;i++)
{
ll tot=0;
f[i][j]=f[f[i][j-1]][j-1];
pai[++tot]=mx1[i][j-1];
pai[++tot]=mx2[i][j-1];
pai[++tot]=mx1[f[i][j-1]][j-1];
pai[++tot]=mx2[f[i][j-1]][j-1];
sort(pai+1,pai+tot,cmp);
mx1[i][j]=pai[1];
for(ll k=2;k<=tot;k++)
if(pai[k]!=pai[1])
{mx2[i][j]=pai[k];break;}
}
}
void lca(ll x,ll y,ll kk)
{
ll ans1=0,ans2=0;
if(dep[x]<dep[y]) swap(x,y);
ll s=dep[x]-dep[y];
for(ll i=0;i<=19;i++)
if(s&(1<<i))
{
if(mx1[x][i]>ans1)
{
ans2=ans1,ans1=mx1[x][i];
if(mx2[x][i]>ans2)
ans2=mx2[x][i];
}
else if(mx1[x][i]>ans2)
ans2=mx1[x][i];
x=f[x][i];
}
if(x==y)
{
if(ans1!=ff[kk].z)
anss=min(ff[kk].z-ans1,anss);
else
anss=min(ff[kk].z-ans2,anss);
return;
}
for(ll i=19;i>=0;i--)
{
if(f[x][i]!=f[y][i])
{
if(mx1[x][i]>ans1)
{
ans2=ans1,ans1=mx1[x][i];
if(mx2[x][i]>ans2)
ans2=mx2[x][i];
}
else if(mx1[x][i]>ans2)
ans2=mx1[x][i];
if(mx1[y][i]>ans1)
{
ans2=ans1,ans1=mx1[y][i];
if(mx2[y][i]>ans2)
ans2=mx2[y][i];
}
else if(mx1[y][i]>ans2)
ans2=mx1[y][i];
x=f[x][i];
y=f[y][i];
}
}
if(mx1[x][0]>ans1)
{
ans2=ans1,ans1=mx1[x][0];
if(mx2[x][0]>ans2)
ans2=mx2[x][0];
}
else if(mx1[x][0]>ans2)
ans2=mx1[x][0];
if(mx1[y][0]>ans1)
{
ans2=ans1,ans1=mx1[y][0];
if(mx2[y][0]>ans2)
ans2=mx2[y][0];
}
else if(mx1[y][0]>ans2)
ans2=mx1[y][0];
//cout<<ans1<<' '<<ans2<<endl;
if(ans1!=ff[kk].z)
anss=min(anss,ff[kk].z-ans1);
else
anss=min(anss,ff[kk].z-ans2);
}
int main()
{
ll cnt=0;
cin>>n>>m;
for(ll i=1;i<=n;i++)
fa[i]=i;
for(ll i=1;i<=m;i++)
scanf("%lld%lld%lld",&ff[i].x,&ff[i].y,&ff[i].z);
sort(ff+1,ff+1+m);
for(ll i=1;i<=m;i++)
{
ll x=ff[i].x,y=ff[i].y;
ll f1=find(x),f2=find(y);
if(f1!=f2)
{
vis[i]=1;
cnt++;
fa[f1]=f2;
ans+=ff[i].z;
add(x,y,ff[i].z);
add(y,x,ff[i].z);
}
if(cnt==n-1) break;
}
dep[1]=1;
dfs(1,0);
zuxian();
for(ll i=1;i<=m;i++)
{
if(vis[i]) continue;
ll x=ff[i].x,y=ff[i].y;
lca(x,y,i);
}
cout<<ans+anss;
}
博主蒟蒻,可以随意转载,但必须附上原文链接k-z-j。


