Bellman-Ford算法【模板】

题目描述

如题，给出一个有向图，请输出从某一点出发到所有点的最短路径长度。

输入输出格式

输入格式：

第一行包含三个整数N、M、S，分别表示点的个数、有向边的个数、出发点的编号。

接下来M行每行包含三个整数Fi、Gi、Wi，分别表示第i条有向边的出发点、目标点和长度。

输出格式：

一行，包含N个用空格分隔的整数，其中第i个整数表示从点S出发到点i的最短路径长度（若S=i则最短路径长度为0，若从点S无法到达点i，则最短路径长度为2147483647）

输入输出样例

输入样例#1：复制

4 6 1
1 2 2
2 3 2
2 4 1
1 3 5
3 4 3
1 4 4

输出样例#1：复制

0 2 4 3

说明

时空限制：1000ms,128M

数据规模：

对于20%的数据：N<=5，M<=15

对于40%的数据：N<=100，M<=10000

对于70%的数据：N<=1000，M<=100000

对于100%的数据：N<=10000，M<=500000

样例说明：

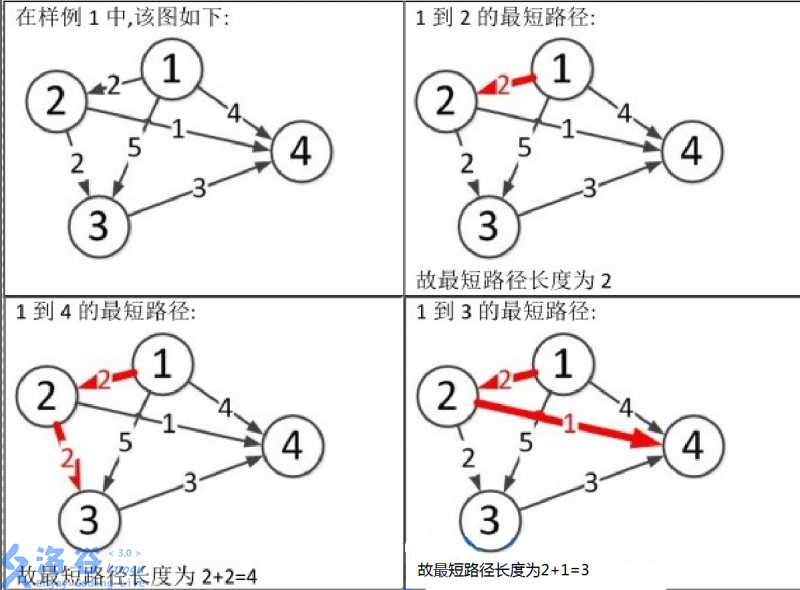
图片1到3和1到4的文字位置调换

代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <algorithm>
#include <vector>
#include <set>
#include <map>
#define INF 2147483647
#define LL long long
using namespace std;
const int maxn=500005;
LL dis[10005];
int u[maxn],v[maxn],w[maxn];
int main()
{
    int n,m,s,k;
    scanf("%d %d %d",&n,&m,&s);
    for(int i=1;i<=n;i++){
        dis[i]=INF;
    }
    dis[s]=0;
    for(int i=1;i<=m;i++){
        scanf("%d %d %d",&u[i],&v[i],&w[i]);
    }
    for(k=1;k<=n-1;k++){//做n-1次松弛，因为任意两点之间的最短路最多包含n-1条边
        int flag=0;
        for(int i=1;i<=m;i++){
            if(dis[v[i]]>dis[u[i]]+w[i]){
                dis[v[i]]=dis[u[i]]+w[i];
                flag=1;
            }
        }
        if(!flag) break;
    }
    for(int i=1;i<n;i++){
        printf("%d ",dis[i]);
    }
    printf("%d\n",dis[n]);
    return 0;
}