Large-Scale Multiobjective Optimization via Reformulated Decision Variable Analysis
作者的主要贡献/工作:
- 提出了一种基于重构的 DVA 方法,用于高效的大规模多目标优化。具体来说,DVA 过程被重新表述为具有二元决策变量的 MOP,该二元决策变量指示交互的收敛相关决策变量的分组结果。然后,在优化过程中可以交互地近似不同变量的相互作用以节省有限元。通过替换实验验证了所提出的基于重构的 DVA 方法的有效性。
- 提出了一种基于DVA重构的进化大规模多目标优化框架,即LERD。它利用基于重构的 DVA 来加速 LSMOP 的优化,其中决策变量的不同子向量被独立优化。消融研究揭示了拟议的 LERD 中每个组成部分的重要性。与六个代表性大型 MOEA 的实验比较验证了 LERD 的有效性和效率。
分组技术:
- Nonheuristic(非启发式):不用花费任何的FE但是也不考虑变量之间的相互作用,(顺序分组,随机分组,order 分组)。
- Heuristic(启发式):消耗大量的FE来评估变量之间的关系。
作者基于MOEA/DVA的变量分析的思想,将决策变量根据目标空间的聚类结果分组,然后使用启发式变量分组技术对同类型变量分组,最后每个子集可以独立优化
Motivation
目前已知的DVA都是先假定变量之间的相互作用关系可以静态获得,这就需要大量的抽样解来得到精确的变量关系在复杂的MOP中。
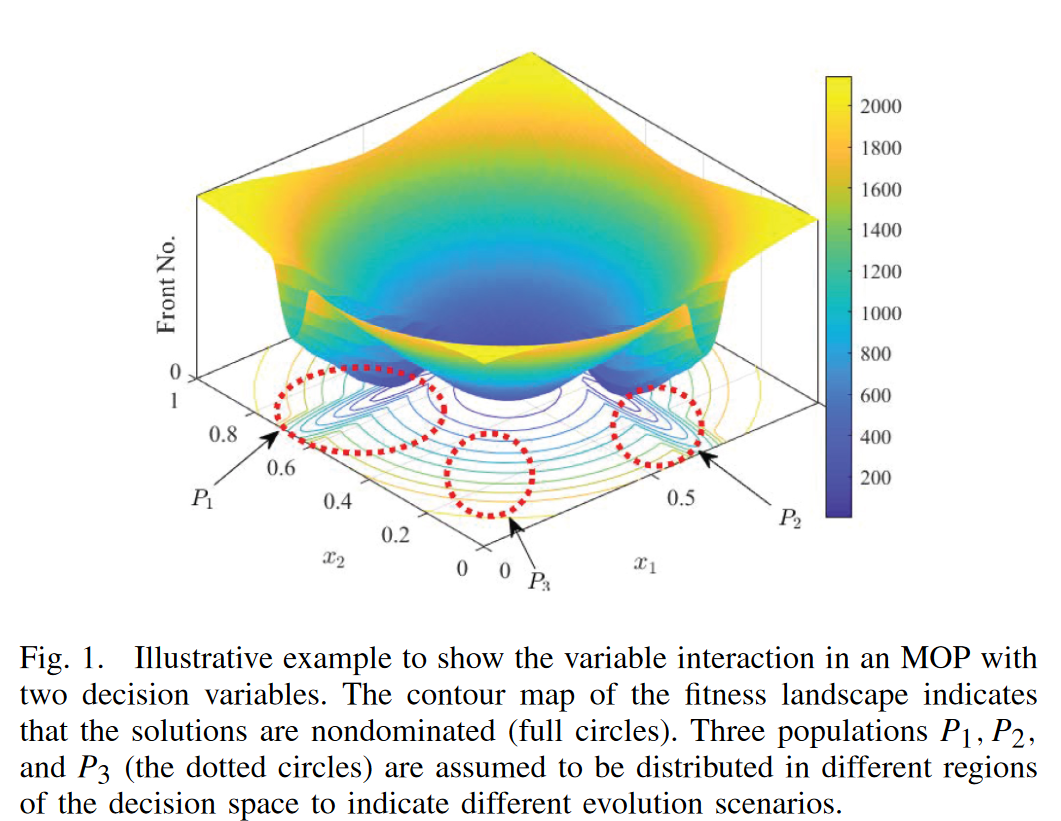
在这个例子中,我们假设有三个种群,P1, P2和P3,分布在不同的决策空间区域。从局部信息的角度来看,对于P1和P2,与收敛相关的优化主要涉及到x1和x2。换句话说,这两个决策变量是不相互作用的,这两个决策变量的独立优化也可以有效地导致全局最优。但是,由于P3的两个决策变量是相互作用的,所以这两个决策变量联合优化的收敛速度是最快的。
因此,在局部区域,动态逼近的变量相互作用可能与精确的全局相互作用不同。如果变量相互作用随演化动态逼近,则moea将沿着最陡的收敛路径加速大规模优化。(意思就是P3的位置\(x_1,x_2\)有相互作用,一起优化可以加速逼近局部最优,也就是说变量之间的关系系在局部范围内是动态变化的)。
作者提出基础重构的决策变量分析的大规模多目标优化有两个目的。
- 我们的目标是在现有的基于dva的大规模moea中节省FEs。该方法不是预先检测所有变量的交互关系,而是试图通过优化一个重新表述的问题来获得一组相互作用的决策变量。
- 期望在使用可接受的FEs数量的同时动态识别进化过程中的可变交互作用。在基于dva的moea中,动态机制有望遵循局部区域最快的收敛路径,而不是跟踪固定变量的相互作用。
Method



\(f^l,f^u\)目标空间上下界。\(x^l,x^u\)决策变量上下界。
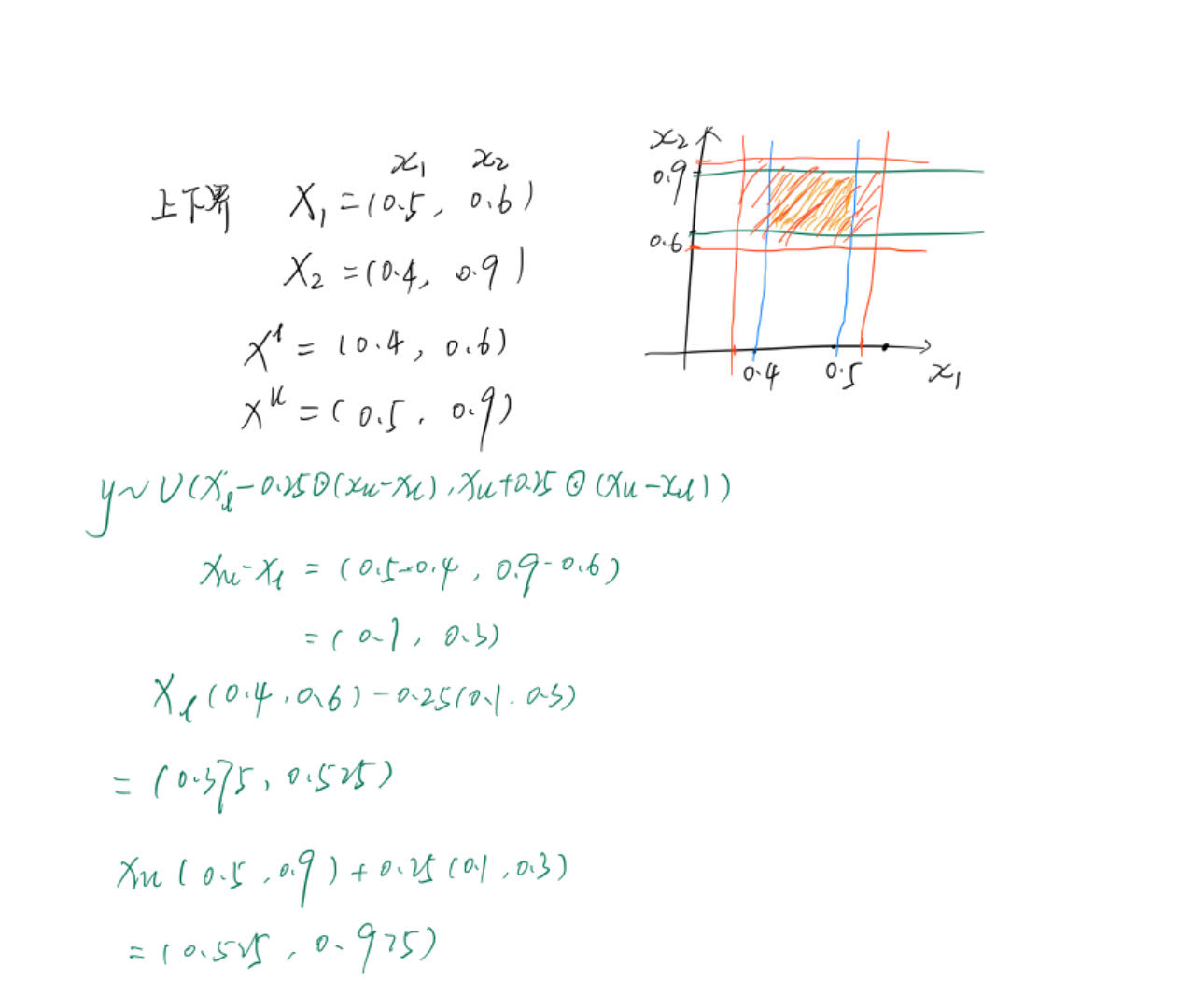
所以algorithm 3的line 9 就相当于将决策变量空间放大了0.25倍数。
然后line 10就相当于一个新的算子在生成新的子代。
但是但是但是注意不是简单的新算子。
由于二元变量组\(b_i\)的存在:

由于y是在红色区域的采样空间均匀采样所以相当于随机分组然后探测分组的变量相关性。\(P_r\)就是所有的采样解。这里和MOEA/DVA(MD)的区别在于,MD的到抽样解继续分析分组后解的相关性然后得到subcomponent。然后才开始优化。LERD在边探测变量关系的过程中也在同步进行优化,(因为他会保留好的解的分组情况也就是\(b_i\)也就是返回的Q保留了适应度值对应分组情况) 。
接下来就简单很多了,algorithm 2中的在迭代次数gen内生成新的B然后进入algorithm 3然后合并新的子代,环境选择。gen轮之后输出\(P_r,B\)。
回到algorithm 1 中line 3筛选得到最新的种群P。我们有理由认为种群p中的个体对应的分组B(\(b_i\))是一个有助于收敛性的变量分组,可以在这个分组的情况下继续繁衍出新的子代。然后环境选择。在进入与之相反的分组(和收敛性相反的分组那必然是有助于多样性的,因为变量关系就这两个。)
在\(n_b\)次迭代完成后将得到的种群嵌入MOEA中得到最终解。





