数据结构与算法(七):递归
斐波那契数列
迭代实现
如果说兔子在出生两个月后,就有繁殖能力,一对兔子每个月能生出一对小兔子来。假
设所有兔子都不会死去,能够一直干下去,那么一年以后可以繁殖多少对兔子呢

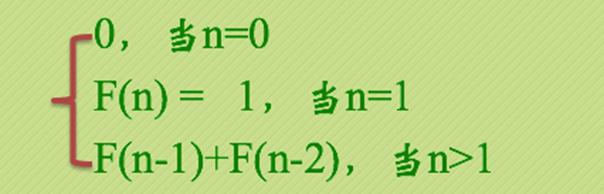
int Fib(int i) { if( i < 2 ) return i == 0 ? 0 : 1; return Fib(i-1) + Fib(i-2); } |
递归的定义
递归事实上就是:函数自己调用自己
递归函数:
一个直接调用自己或通过一系列的调用语句间接地调用自己的函数
每个递归定义必须至少有一个条件,当满足这个条件时递归不再进行,即函数不再调用自身而是返回值
迭代和递归的区别:
- 迭代使用的是循环结构
- 递归使用的是选择结构
计算n的阶乘n!:
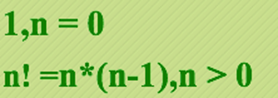
int factorial( n ) { if( 0 == n ) return 1; else return n * factorial( n - 1 ); } |
实例分析
编写一个递归函数,实现将输入的任意长度的字符串反向输出的功能。例如输入字符串FishC,则输出字符串ChsiF
void function(c) { scanf("%c",&c); if(c != '#') function(c); if(c !='#') printf("%c",c); } |
折半查找法
折半查找的基本思想是:减小查找序列的长度,分而治之地进行关键字的查找
折半查找的实现过程是:先确定待查找记录的所在范围,然后逐渐缩小这个范围,直到找到该记录或查找失败(查无该记录)为止
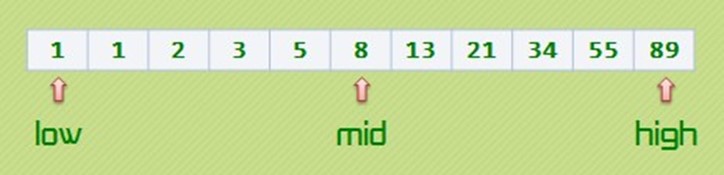
key = 55,大于 8
于是我们执行 low = mid+1; mid = (low+high)/2
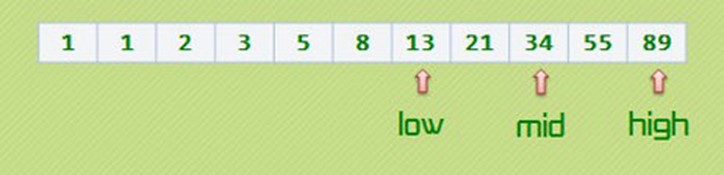
将 mid 所指的 34 与 key 进行比较,仍然 mid < key
low = mid+1; mid = (low+high)/2;

仍然将 mid 所指的元素与 key 进行比较
结果相等,查找成功,返回 mid 的指针值,程序结束
折半查找递归:
int HalfSearch( int str[], int low,int high, int key ) { if(low>high) return -1; int mid = (low+high)/2;
if(str[mid] == key) { return mid; } else if(str[mid]<key) { HalfSearch(str,mid+1,high,key); } else if(str[mid]>key) { HalfSearch(str,low,mid-1,key); } else { return -1; }
}
int main() { int str[11] = {1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89}; int n, Digui = 0; printf("请输入待查找的关键字: "); scanf("%d", &n); Digui = HalfSearch(str,0,11,n); if( -1 != Digui ) { printf("查找成功,关键字 %d 所在的位置是: %d\n", n, Digui); } else { rintf("查找失败!\n"); } return 0; } |
汉诺塔问题

- 先讲前63个盘子移动到Y上确保大盘在小盘下
- 再将最底下的第64个盘子移动到Z上
- 最后将Y上的63个盘子移动到Z上
问题一的圆盘移动步骤为:
先将前62个盘子移动到Z上,确保大盘在小盘下。
再将最底下的第63个盘子移动到Y上。
最后将Z上的62个盘子移动到Y上。
问题二的圆盘移动步骤为:
先将前62个盘子移动到X上,确保大盘在小盘下。
再将最底下的第63个盘子移动到Z上。
最后将X上的62个盘子移动到Y上。
#include <stdio.h> void Move(int n,char x,char y,char z) { if(n==1) { printf("%c-->%c\n",x,z); } else { Move(n-1,x,z,y);//将n-1个盘子借助z从x移到y上 printf("%c-->%c\n",x,z);//将第n个盘子从x移到z上 Move(n-1,y,x,z);//将 n-1个盘子借助x从y移到z上 } } int main() { int n; printf("请输入层数:"); scanf("%d",&n);
printf("移动步骤:"); Move(n,'X','Y','Z'); } |
八皇后问题
#include <stdio.h>
int count = 0;
int notDanger(int row, int j, int (*chess)[8]) { int i, k, flag1 = 0, flag2 = 0, flag3 = 0, flag4 = 0, flag5 = 0;
// 判断列方向 for (i = 0; i < 8; i++) { if (*(*(chess + i) + j) != 0) { flag1 = 1; break; } }
// 判断左上方 for (i = row, k = j; i >= 0 && k >= 0; i--, k--) { if (*(*(chess + i) + k) != 0) { flag2 = 1; break; } }
// 判断右下方 for (i = row, k = j; i < 8 && k < 8; i++, k++) { if (*(*(chess + i) + k) != 0) { flag3 = 1; break; } }
// 判断右上方 for (i = row, k = j; i >= 0 && k < 8; i--, k++) { if (*(*(chess + i) + k) != 0) { flag4 = 1; break; } }
// 判断左下方 for (i = row, k = j; i < 8 && k >= 0; i++, k--) { if (*(*(chess + i) + k) != 0) { flag5 = 1; break; } }
if (flag1 || flag2 || flag3 || flag4 || flag5) { return 0; } else { return 1; } }
// 参数row: 表示起始行 // 参数n: 表示列数 // 参数(*chess)[8]: 表示指向棋盘每一行的指针 void EightQueen(int row, int n, int (*chess)[8]) { int chess2[8][8], i, j;
for (i = 0; i < 8; i++) { for (j = 0; j < 8; j++) { chess2[i][j] = chess[i][j]; } }
if (8 == row) { printf("第 %d 种\n", count + 1); for (i = 0; i < 8; i++) { for (j = 0; j < 8; j++) { printf("%d ", *(*(chess2 + i) + j)); } printf("\n"); } printf("\n"); count++; } else { for (j = 0; j < n; j++) { if (notDanger(row, j, chess)) // 判断是否危险 { for (i = 0; i < 8; i++) { *(*(chess2 + row) + i) = 0; }
*(*(chess2 + row) + j) = 1;
EightQueen(row + 1, n, chess2); } } } }
int main() { int chess[8][8], i, j;
for (i = 0; i < 8; i++) { for (j = 0; j < 8; j++) { chess[i][j] = 0; } }
EightQueen(0, 8, chess);
printf("总共有 %d 种解决方法!\n\n", count);
return 0 |

