数据结构与算法(六):队列
队列
什么是队列?

定义
- 只允许在一端进行插入操作,而在另一端进行删除操作的线性表
- 与栈相反,队列是一种先进先出( First In First Out)(FIFO)的线性表
- 与栈相投的是,队列也是一种重要的线性结构,实现一个队列需要顺序表或链表作为基础
队列的链式存储结构
定义
队列既可以用链表,也可以用顺序表
栈一般用顺序表,而队列常用链表来实现,简称链队列
typedef struct QNode { ElemType data; struct QNode *next; } QNode, *QueuePtr;
typedef struct { QueuePtr front, rear; // 队头、尾指针 } LinkQueue; |
队头指针指向链队列的头节点,队尾指针指向终端结点

空队列时,front和rear都指向头结点
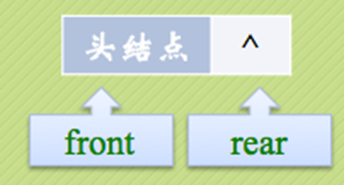
创建一个队列
- 在内存中创建一个头节点
- 将队列的头指针和尾指针都指向这个生成的头节点,因为此时是空队列
initQueue(LinkQueue *q) { q->front=q->rear=(QueuePtr)malloc(sizeof(QNode)); if( !q->front ) exit(0); q->front->next = NULL; } |
入队列的操作
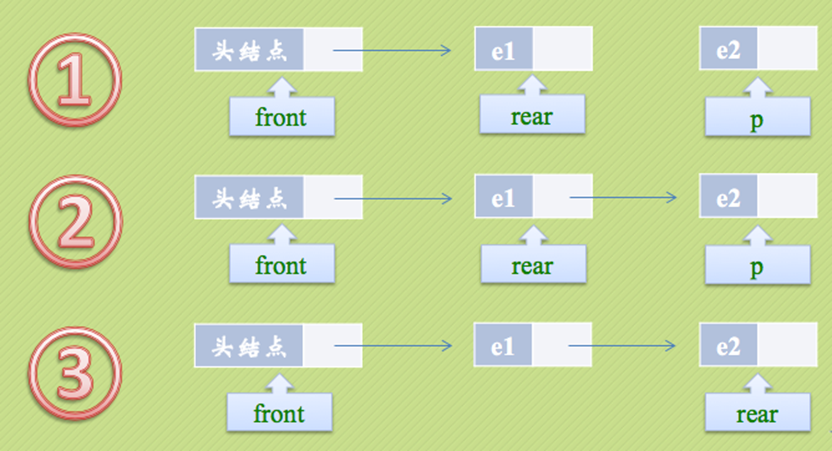
InsertQueue(LinkQueue *q, ElemType e) { QueuePtr p; p = (QueuePtr)malloc(sizeof(QNode)); if( p == NULL ) exit(0); p->data = e;//e赋值给新节点的数据 p->next = NULL;//新节点指向队尾空 q->rear->next = p;//q队列的队尾的next指向p q->rear = p;//q队列队尾等于p } |
出队列操作
将队列中的第一个元素移出,队头指针不发生改变,改变头结点的next指针即可
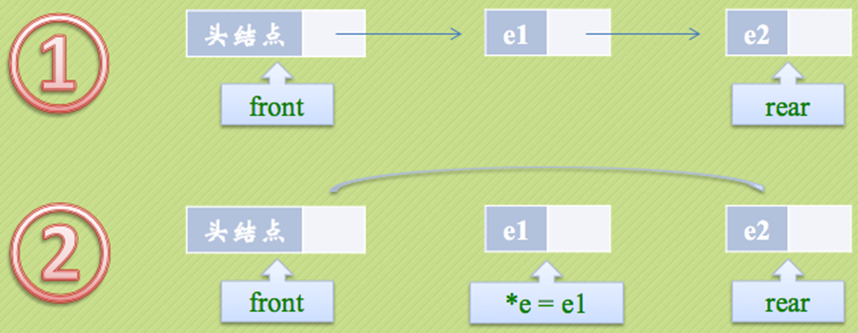
如果原队列只有一个元素,那么我们就应该处理一下队尾指针
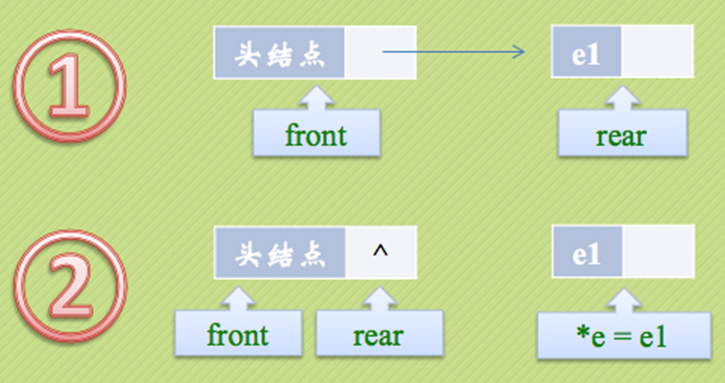
DeleteQueue(LinkQueue *q, ELemType *e) { QueuePtr p; if( q->front == q->rear //如果为空队列 return; p = q->front->next;//p=q *e = p->data;//返回出队数据 q->front->next = p->next;//q头节点next 指向 p的下一个元素 if( q->rear == p )//如果只有一个元素 q->rear = q->front; free(p); } |
销毁一个队列
由于链队列建立在内存的动态区
因此当一个队列不在有用时应当把它及时销毁,以免过多的占用内存空间
DestroyQueue(LinkQueue *q) { while( q->front ) { q->rear = q->front->next;//清空队列 free( q->front );//释放队列空间 q->front = q->rear;//空队列 } } |
课后作业
编写一个链队列,任意输入一串字符,以#作为结束标志,然后将队列中的元素显示到屏幕上
#include <stdio.h> #include <stdlib.h>
typedef char ElemType;
typedef struct QNode { ElemType data; struct QNode *next; } QNode, *QueuePtr;
typedef struct { QueuePtr front, rear; } LinkQueue;
initQueue(LinkQueue *q) { q->front = q->rear = (QueuePtr)malloc(sizeof(QNode)); if (!q->front) exit(0); q->front->next = NULL; }
InsertQueue(LinkQueue *q, ElemType e) { QueuePtr p; p = (QueuePtr)malloc(sizeof(QNode)); if (p == NULL) exit(0); p->data = e; p->next = NULL; q->rear->next = p; q->rear = p; }
DeleteQueue(LinkQueue *q, ElemType *e) { QueuePtr p;
if (q->front == q->rear) return;
p = q->front->next; *e = p->data; q->front->next = p->next;
if (q->rear == p) q->rear = q->front; free(p); }
int main() { ElemType c; LinkQueue q;
printf("输入一串字符,以#结束: "); scanf("%c", &c);
initQueue(&q);
while (c != '#') { InsertQueue(&q, c); scanf("%c", &c); }
printf("队中元素:"); while (q.front != q.rear) { DeleteQueue(&q, &c); printf("%c", c); } return 0; } |
队列的顺序存储结构
一个队列有n个元素,则顺序存储的队列需建立一个大于n的存储单元,
并把队列的所有元素存储在数组的前n个单元,数组下标为0的一端则是队头。
入队列操作
其实就是在队尾追加一个元素,不需要任何移动,时间复杂度为O(1)

出队列操作
每次出队列操作所有元素都要向前移动

一群人在排队买火车票,前边的人买好了离开,后面的人就要全部向前一步补上空位。
假溢出
如果我们不去限制队头一定要在下标为0的位置,那么出队列的操作就不需要移动全体元素

但是如果继续入队列,就会出现数组越界的错误

事实上我们有0和1两个下标还空着,这叫假溢出
循环队列
循环队列定义
为充分利用向量空间,克服"假溢出"现象的方法是:
- 将向量空间想象为一个首尾相接的圆环,并称这种向量为循环向量
- 存储在其中的队列称为循环队列(Circular Queue)
- 循环队列是把顺序队列首尾相连,把存储队列元素的表从逻辑上看成一个环,称为循环队列
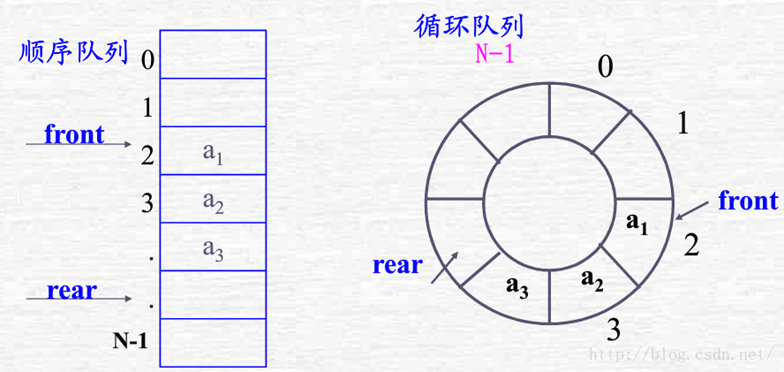
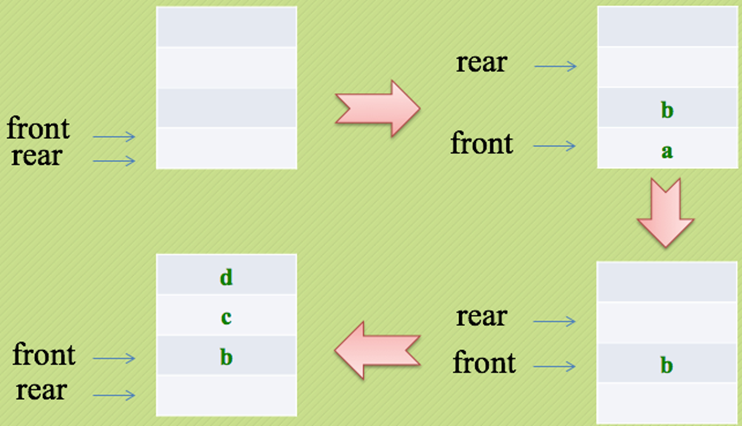
灵活改变front和rear指针即可
#define MAXSIZE 100 typedef struct { ElemType *base; // 用于存放内存分配基地址 // 这里你也可以用数组存放 int front; int rear; } |
循环队列初始化
initQueue(cycleQueue *q) { q->base = (ElemType *) malloc (MAXSIZE * sizeof(ElemType)); if( !q->base ) exit(0); q->front = q->rear = 0; } |
循环队列入队列操作
InsertQueue(cycleQueue *q, ElemType e) { if( (q->rear+1)%MAXSIZE == q->front ) return; // 队列已满 q->base[q->rear] = e; q->rear = (q->rear+1) % MAXSIZE; } |
循环队列出队列操作
DeleteQueue(cycleQueue *q, ElemType *e) { if( q->front == q->rear ) return ; // 队列为空 *e = q->base[q->front]; q->front = (q->front+1) % MAXSIZE; } |

