数据结构与算法（五）：栈

栈的定义

官方定义：栈（Stack）是一个后进先出（Last in first out，LIFO）的线性表，它要求只在表尾进行删除和插入操作

小甲鱼的定义：所谓的栈，其实也就是一个特殊的线性表（顺序表、链表），但是它再操作上有一些特殊的要求和限制：

• 栈的元素必须"后进先出"
• 栈的操作只能再这个线性表的表尾进行
• 注：对于栈来说，这个表尾称为栈的栈顶（top），相应的表头称为栈底（bottom）

   

栈的插入和删除操作

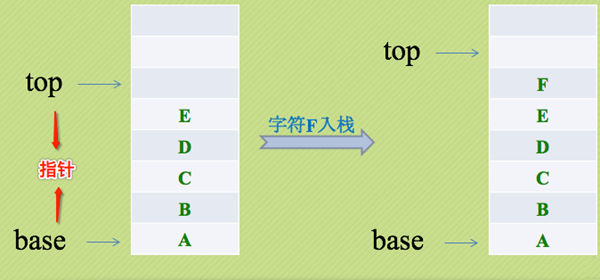
• 栈的插入操作（Push），叫做进栈，也称为压栈，入栈 类似子弹放入弹夹的动作
• 栈的删除操作（Pop），叫做出栈，也称为弹栈 如同单价中的子弹出夹
• 图片演示：

  

   

栈的顺序存储结构

   

定义一个顺序存储的栈

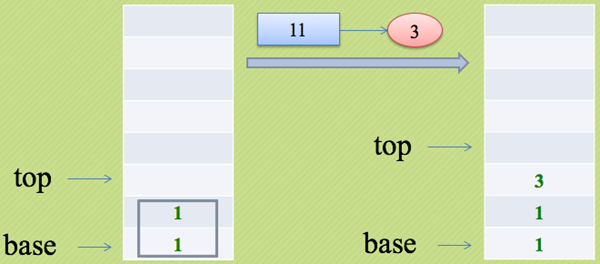
• base是指向栈底的指针变量
• top是指向栈顶的指针变量
• stackSize是指栈的当前可使用的最大容量

typedef struct

{

    ElemType *base;

    ElemType *top;

    int stackSize;

}sqStack;

   

另一种声明方法

typedef int ElemType;

typedef struct

{

    ElemType data[MAXSIZE];

    int top; //用于标注栈顶位置

    int stackSize;

}

   

   

初始化创建一个栈

#define STACK_INIT_SIZE 100

initStack(sqStack *s)

{

    s->base = (ElemType *)malloc( STACK_INIT_SIZE * sizeof(ElemType) );

    if( !s->base )

        exit(0);

    s->top = s->base; // 最开始，栈顶就是栈底

    s->stackSize = STACK_INIT_SIZE;

}

   

入栈操作

• 入栈操作又叫压栈操作，就是向栈中存放数据
• 入栈操作要在栈顶进行，每次向栈中压入一个数据。top指针就要+1，直到栈满为止

#define SATCKINCREMENT 10

Push(sqStack *s, ElemType e)

{

// 如果栈满，追加空间

if( s->top – s->base >= s->stackSize )

{

s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));

if( !s->base )

exit(0);

s->top = s->base + s->stackSize; // 设置栈顶

s->stackSize = s->stackSize + STACKINCREMENT; // 设置栈的最大容量

}

*(s->top) = e;

s->top++;

}

   

   

出栈操作

• 出栈操作就是在栈顶取出数据，栈顶指针随之下移
• 每当栈内弹出一个数据，栈的当前容量就-1

Pop(sqStack *s, ElemType *e)

{

    if( s->top == s->base ) // 栈已空空是也

    return;

    *e = *--(s->top);

}

   

清空栈

就是将栈中的元素全部作废，但栈本身的物理空间并不发生改变（不是销毁）

因此我们只要将s->top的内容赋值为s->base即可，这样s->base等于s->top，也就表明这个栈是空的了

ClearStack(sqStack *s)

{

    s->top = s->base;

}

   

销毁栈

与清空栈不同，销毁一个栈是要释放带哦该栈所占据的物理内存空间

DestroyStack(sqStack *s){

    int i, len;

    len = s->stackSize;

    for( i=0; i < len; i++ ){

    free( s->base );

    s->base++;

    }

    s->base = s->top = NULL;

    s->stackSize = 0;

}

   

计算栈的当前容量

s.stackSize是栈的最大容量，并不是栈的当前容量

计算栈的当前容量也就是计算栈中元素的个数，只要计算s.top - s.base即可

int StackLen(sqStack s)

{

    return(s.top – s.base); // 初学者需要重点讲解

}

   

   

实例

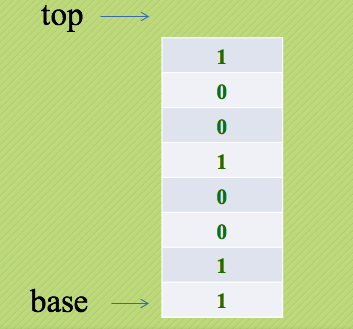
二进制转换为十进制数

计算方法: (XnXn-1……X3X2X1)2 = X1*2^0+X2*2^1+…+Xn*2^(n-1)

一个二进制数要转换为相应的十进制数，就是从最低位起用每一位去乘以对应位的积，也就是说用第n位去乘以2^(n-1)，然后全部加起来

#include <stdio.h>

#include <stdlib.h>

#include <math.h>

#define STACK_INIT_SIZE 20

#define STACKINCREMENT 10

typedef char ElemType;

typedef struct

{

        ElemType *base;

        ElemType *top;

        int stackSize;

}sqStack;

void InitStack(sqStack *s)

{

        s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));

        if( !s->base )

        {

                exit(0);

        }

   

        s->top = s->base;

        s->stackSize = STACK_INIT_SIZE;

}

void Push(sqStack *s, ElemType e)

{

        if( s->top - s->base >= s->stackSize )

        {

                s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));

                if( !s->base )

                {

                        exit(0);

                }

        }

   

        *(s->top) = e;

        s->top++;

}

void Pop(sqStack *s, ElemType *e)

{

        if( s->top == s->base )

        {

                return;

        }

        *e = *--(s->top);

}

int StackLen(sqStack s)

{

        return (s.top - s.base);

}

int main()

{

        ElemType c;

        sqStack s;

        int len, i, sum = 0;

        InitStack(&s);

        printf("请输入二进制数，输入#符号表示结束！\n");

        scanf("%c", &c);

        while( c != '#' )

        {

                Push(&s, c);

                scanf("%c", &c);

        }

        getchar(); // 把'\n'从缓冲区去掉

        len = StackLen(s);

        printf("栈的当前容量是: %d\n", len);

        for( i=0; i < len; i++ )

        {

                Pop(&s, &c);

                sum = sum + (c-48) * pow(2, i);

        }

        printf("转化为十进制数是: %d\n", sum);

        return 0;

   

二进制转八进制数

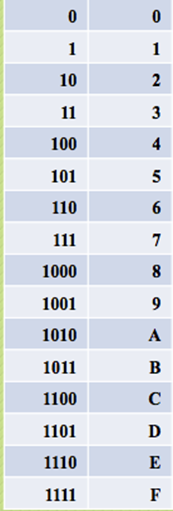
一个十六进制数最多占4bit，一个字节（8bit）刚好用两个十六进制数完全表示，节省了显示空间

#include <stdio.h>

#include <stdlib.h>

#include <math.h>

#define STACK_INIT_SIZE 20

#define STACKINCREMENT 10

typedef char ElemType;

typedef struct

{

        ElemType *base;

        ElemType *top;

        int stackSize;

}sqStack;

// 函数功能：初始化栈

// 参数*s：栈的地址

void InitStack(sqStack *s)

{

        s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));

        if( !s->base )

        {

                exit(0);

        }

   

        s->top = s->base;

        s->stackSize = STACK_INIT_SIZE;

}

// 函数功能：入栈操作

// 参数*s：栈的地址

// 参数e：待压入栈的元素

void Push(sqStack *s, ElemType e)

{

        if( s->top - s->base >= s->stackSize )

        {

                s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));

                if( !s->base )

                {

                        exit(0);

                }

   

                s->top = s->base + s->stackSize;

                s->stackSize = s->stackSize + STACKINCREMENT;

        }

   

        *(s->top) = e;

        s->top++;

}

// 函数功能：弹栈操作

// 参数*s：栈的地址

// 参数e：存放从栈里弹出的数据

void Pop(sqStack *s, ElemType *e)

{

        if( s->top == s->base )

        {

                return;

        }

        *e = *--(s->top);

}

// 函数功能：计算栈s的当前长度

// 参数s：栈

int StackLen(sqStack s)

{

        return (s.top - s.base);

}

int main()

{

        ElemType c;

        sqStack s1;

        sqStack s2;

        int len, i, j, sum = 0;

        InitStack(&s1); // 初始化栈s1，用来存放二进制输入

        printf("请输入二进制数，输入'#'号表示结束！\n\n");

        scanf("%c", &c);

        while( c != '#' )

        {

                if( c=='0' || c=='1' ) // 检查输入是否二进制

                        Push(&s1, c);

                scanf("%c", &c);

        }

        getchar(); // 把'\n'从缓冲区去掉

        len = StackLen(s1);

        InitStack(&s2); // 初始化栈s2，用来存放转换的八进制

        for( i=0; i < len; i+=4 )

        {

                for( j=0; j < 4; j++ )

                {

                        Pop( &s1, &c ); // 取出栈顶元素

                        sum = sum + (c-48) * pow(2, j);

   

                        if( s1.base == s1.top )

                        {

                                break;

                        }

                }

                switch( sum )

                {

                        case 10: sum = 'A'; break;

                        case 11: sum = 'B'; break;

                        case 12: sum = 'C'; break;

                        case 13: sum = 'D'; break;

                        case 14: sum = 'E'; break;

                        case 15: sum = 'F'; break;

                        default: sum += 48;

                }

                Push( &s2, sum );

                sum = 0;

        }

        printf("\n转化为十六进制数是: ");

        while( s2.base != s2.top )

        {

                Pop( &s2, &c );

                printf("%c", c);

        }

        printf("(H)\n"

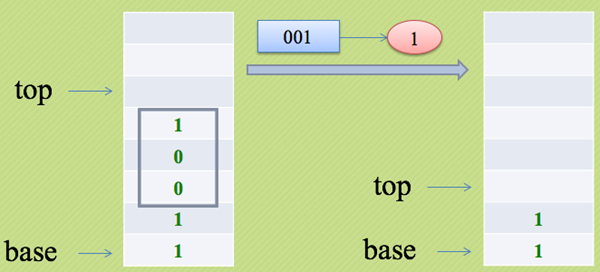
二进制转八进制

进行二进制到八进制的转换时，要将二进制数的每三位抓换成一个八进制数来表示，然后按顺序输出即可

   

   

   

#include <stdio.h>

#include <stdlib.h>

#include <math.h>

#define STACK_INIT_SIZE 20

#define STACKINCREMENT 10

typedef char ElemType;

typedef struct

{

        ElemType *base;

        ElemType *top;

        int stackSize;

}sqStack;

// 函数功能：初始化栈

// 参数*s：栈的地址

void InitStack(sqStack *s)

{

        s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));

        if( !s->base )

        {

                exit(0);

        }

        s->top = s->base;

        s->stackSize = STACK_INIT_SIZE;

}

// 函数功能：入栈操作

// 参数*s：栈的地址

// 参数e：待压入栈的元素

void Push(sqStack *s, ElemType e)

{

        if( s->top - s->base >= s->stackSize )

        {

                s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));

                if( !s->base )

                {

                        exit(0);

                }

                s->top = s->base + s->stackSize;

                s->stackSize = s->stackSize + STACKINCREMENT;

        }

   

        *(s->top) = e;

        s->top++;

}

// 函数功能：弹栈操作

// 参数*s：栈的地址

// 参数e：存放从栈里弹出的数据

void Pop(sqStack *s, ElemType *e)

{

        if( s->top == s->base )

        {

                return;

        }

        *e = *--(s->top);

}

// 函数功能：计算栈s的当前长度

// 参数s：栈

int StackLen(sqStack s)

{

        return (s.top - s.base);

}

int main()

{

        ElemType c;

        sqStack s1;

        sqStack s2;

        int len, i, j, sum = 0;

        InitStack(&s1); // 初始化栈s1，用来存放二进制输入

        printf("请输入二进制数，输入'#'号表示结束！\n\n");

        scanf("%c", &c);

        while( c != '#' )

        {

                if( c=='0' || c=='1' ) // 检查输入是否二进制

                        Push(&s1, c);

                scanf("%c", &c);

        }

        getchar(); // 把'\n'从缓冲区去掉

        len = StackLen(s1);

        InitStack(&s2); // 初始化栈s2，用来存放转换的八进制

        for( i=0; i < len; i+=3 )

        {

                for( j=0; j < 3; j++ )

                {

                        Pop( &s1, &c ); // 取出栈顶元素

                        sum = sum + (c-48) * pow(2, j);

   

                        if( s1.base == s1.top )

                        {

                                break;

                        }

                }

                Push( &s2, sum+48 );

                sum = 0;

        }

        printf("\n转化为八进制数是: ");

        while( s2.base != s2.top )

        {

                Pop( &s2, &c );

                printf("%c", c);

        }

        printf("(O)\n"

   

栈的链式存储结构

（简称栈链）

栈的定义

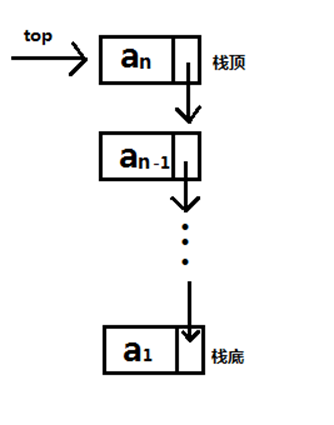
typedef struct StackNode

{

    ElemType data; // 存放栈的数据

    struct StackNode *next;

}StackNode, *LinkStackPtr;

   

typedef struct LinkStack

{

    LinkStackPrt top; // top指针

    int count; // 栈元素计数器

}

   

进栈操作

对于栈链的Push操作，假设元素值为e的新结点是s，top为栈顶指针

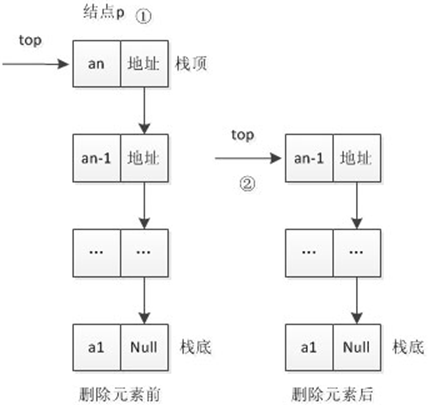
Status Push(LinkStack *s, ElemType e)

{

    LinkStackPtr p = (LinkStackPtr) malloc (sizeof(StackNode));

    p->data = e;

    p->next = s->top;

    s->top = p;

    s->count++;

    return OK;

}

   

出栈操作

对于栈链的Pop操作，假设变量p用来存储要删除的栈顶结点

将栈顶指针下移一位，最后释放p即可

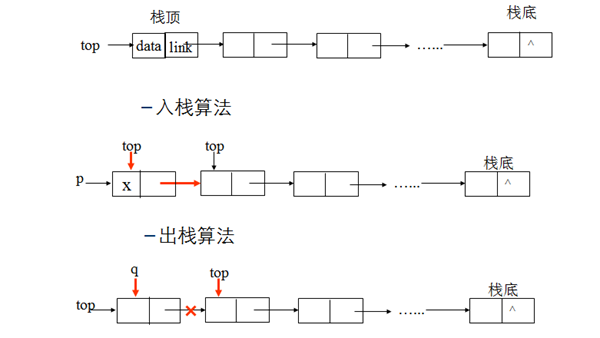
Status Pop(LinkStack *s, ElemType *e)

{

    LinkStackPtr p;

    if( StackEmpty(*s) ) // 判断是否为空栈

    return ERROR;

    *e = s->top->data;

    p = s->top;

    s->top = s->top->next;

    free(p);

    s->count--;

    return OK;

}

   

逆波兰表达式

   

   

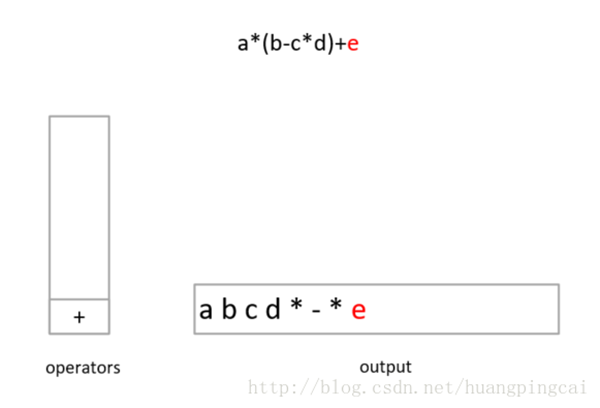
(1-2)*(4+5) 逆波兰表达式：1 2 - 4 5 + *

数字1和2进栈，遇到减号运算符则弹出两个元素进行运算并把结果入栈

   

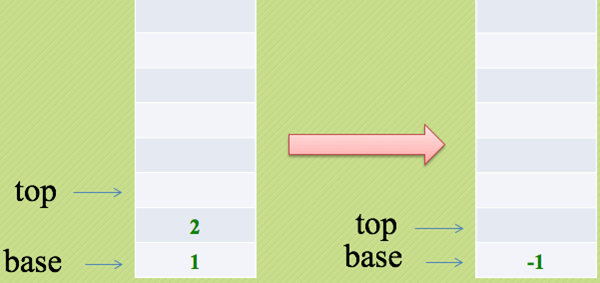
4和5入栈，遇到加号运算符，4和5弹出栈，相加后将结果9入栈

   

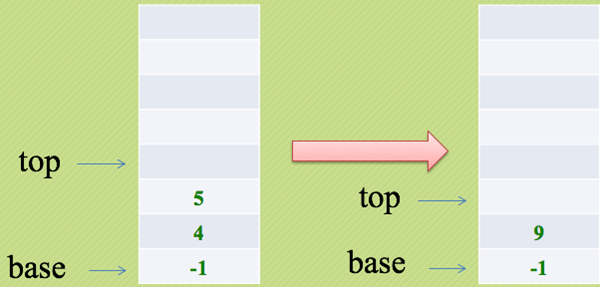
然后又遇到乘法运算符，将9和-1弹出栈进行乘法计算，此时栈空并无数据压栈，-9为最终运算结果！

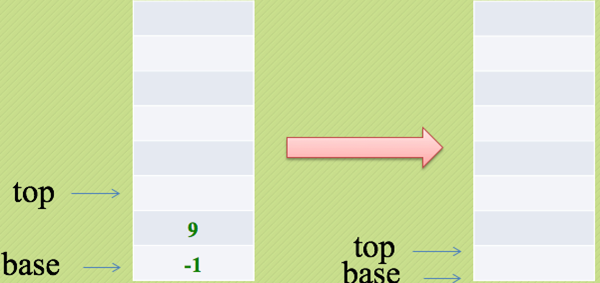
   逆波兰计算器

#include <stdio.h>
#include <ctype.h>
#include <stdlib.h>

#define STACK_INIT_SIZE 20
#define STACKINCREMENT  10
#define MAXBUFFER       10

typedef double ElemType;
typedef struct
{
    ElemType *base;
    ElemType *top;
    int stackSize;
}sqStack;

InitStack(sqStack *s)
{
    s->base = (ElemType *)malloc(STACK_INIT_SIZE * sizeof(ElemType));
    if( !s->base )
        exit(0);

    s->top = s->base;
    s->stackSize = STACK_INIT_SIZE;
}

Push(sqStack *s, ElemType e)
{
    //栈满，追加空间，必须懂 
    if( s->top - s->base >= s->stackSize )
    {
        s->base = (ElemType *)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(ElemType));
        if( !s->base )
            exit(0);

        s->top = s->base + s->stackSize;
        s->stackSize = s->stackSize + STACKINCREMENT;
    }

    *(s->top) = e;      // 存放数据 
    s->top++;
}

Pop(sqStack *s, ElemType *e)
{
    if( s->top == s->base )
        return;

    *e = *--(s->top);   // 将栈顶元素弹出并修改栈顶指针 
}

int StackLen(sqStack s)
{
    return (s.top - s.base);
}

int main()
{
    sqStack s;
    char c;
    double d, e;
    char str[MAXBUFFER];
    int i = 0;

    InitStack( &s );

    printf("请按逆波兰表达式输入计算数据,以#结束\n");
    scanf("%c", &c);

    while( c != '#' )
    {
        while( isdigit(c) || c=='.' )  // 用于过滤数字 
        {
            str[i++] = c;
               str[i] = '\0';
            if( i >= 10 )
            {
                printf("出错，大\n");
                return -1;
            }
            scanf("%c", &c);
            if( c == ' ' )
            {
                d = atof(str);
                Push(&s, d);
                i = 0;
                break;
            }
        }

        switch( c )
        {
            case '+':
                Pop(&s, &e);
                Pop(&s, &d);
                Push(&s, d+e);
                break;
            case '-':
                Pop(&s, &e);
                Pop(&s, &d);
                Push(&s, d-e);
                break;
            case '*':
                Pop(&s, &e);
                Pop(&s, &d);
                Push(&s, d*e);
                break;
            case '/':
                Pop(&s, &e);
                Pop(&s, &d);
                if( e != 0 )
                {
                    Push(&s, d/e);
                }
                else
                {
                    printf("\n出错，0\n");
                    return -1;
                }
                break;
        }

        scanf("%c", &c);
    }

    Pop(&s, &d);
    printf("\n最终计算结果为：%f\n", d);

    return 0;
}
// 5 - (6 + 7) * 8 + 9 / 4
// 5 - 13 * 8 + 9 / 4
// 5 - 104 + 2.25
// -99 + 2.25
// 5 6 7 + 8 * - 9 4 / +

 

中缀表达式转换为后缀表达式

从左到右遍历中缀表达式的每个数字和符号，若是数字则直接输出

若是符号，则判断其与栈顶符号的优先级，是右括号或者优先级低于栈顶符号，则栈顶元素依次出栈并输出，直到遇到左括号或栈空才将吃屎的那个符号入栈

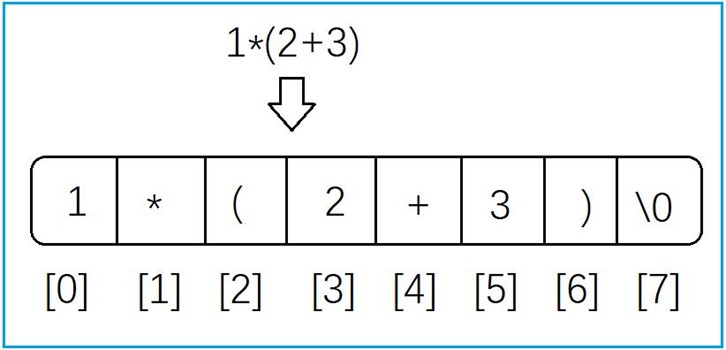
1*(2+3)

• 从左往右扫描中缀表达式

  

• 如果是数字那么将其直接入栈到数组num中

  

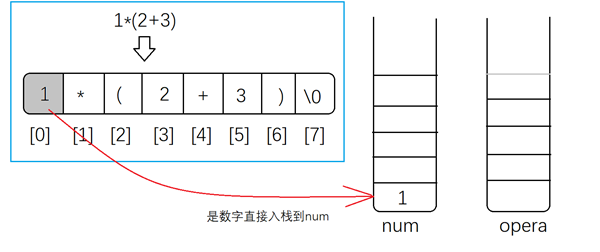
• 如果是运算符 +、-、*、/，若opera栈空或者为左括号直接插入，否则与opera栈顶元素比较优先级，比栈顶高插入，比栈顶低则输出栈顶

  

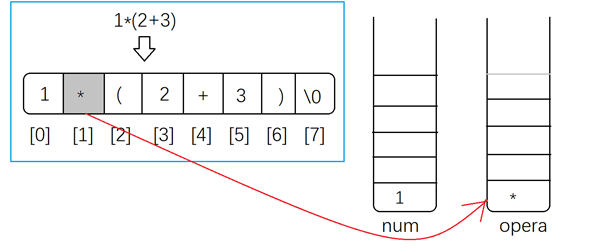
• 如果是左括号直接插入opera栈

  

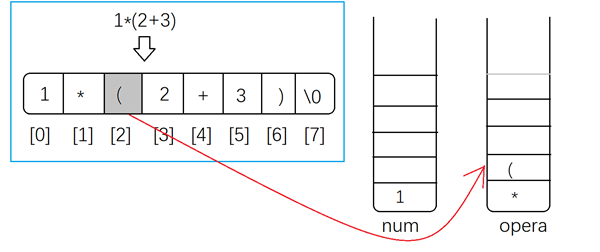
• 如果是右括号将opera中的运算符依次出栈，并入栈到num中，直到遇到左括号

  

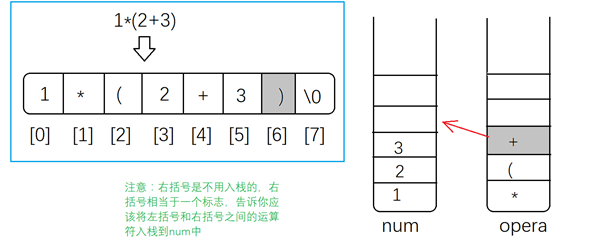
• 如果中缀表达式扫描完了，那么将opera中的操作数依次出栈

  

  

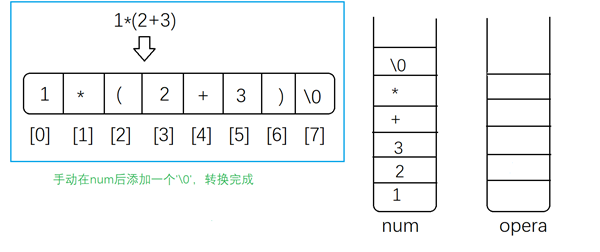
  需要注意的是：opera中操作数，越靠近栈顶，优先级越高