数据结构与算法（四）：线性表二
静态链表
什么是静态链表
用数组代替指针来描述单链表叫做静态链表，这种描述方法叫做游标实现法
最后一个游标指向第一个有数据的下标地址，第一个游标指向第一个没有数据的下标地址
线性表的静态链表存储结构：
#define MAXSIZE 1000
typedef struct
{
ElemType data; // 数据
int cur; // 游标（Cursor）
} Component, StaticLinkList[MAXSIZE];
对静态链表进行初始化相当于初始化数组：
Status InitList(StaticLinkList space) { int i; for( i=0; i < MAXSIZE-1; i++ ) space[i].cur = i + 1; space[MAXSIZE-1].cur = 0; return OK; }
总结：
- 我们对数组的第一个和最后一个元素做特殊处理，他们的data不存放数据
- 我们通常把未使用的数组元素称为备用链表
- 数组的第一个元素，即下标为0的那个元素的cur就存放备用链表的第一个结点的下标
- 数组的最后一个元素，即下标为MAXSIZE-1的cur则存放第一个有数值的元素的下标，相当于单链表中的头结点作用
静态链表的插入操作
1A>5B->2C->3D->4E->06
/* 在静态链表L中第i个元素之前插入新的数据元素e */ Status ListInsert( StaticLinkList L, int i, ElemType e ) { int j, k, l; k = MAX_SIZE - 1; // 数组的最后一个元素 if( i<1 || i>ListLength(L)+1 ) { return ERROR; } j = Malloc_SLL(L);// 获取空闲的第一个分量的下标，j=5 if( j ) { L[j].data = e; //把数据元素e赋值 L(j).data=B for( l=1; l <= i-1; l++ )// 插入到第二个元素之前，所以是i-1，i=2，循环执行1次 { // L[k],l[最后一个元素]，游标指向第一个元素，赋值 K=1 k = L[k].cur; } L[j].cur = L[k].cur;//L[k]的游标=2赋值给L[j]的游标，就是把数据为B的游标改为2 L[k].cur = j;//把j的值赋值给L[k]的下标 L[K].cur=5 就是把数据为A的游标改为5 return OK; } return ERROR; } // 获得空闲分量的下标： int Malloc_SLL(StaticLinkList space) { int i = space[0].cur; if( space[0].cur ) space[0].cur = space[i].cur; // 把它的下一个分量用来作为备用。 return i; }
静态链表的删除操作
/* 删除在L中的第i个数据元素 */ Status ListDelete(StaticLinkList L, int i) { int j, k; if( i<1 || i>ListLength(L) ) { return ERROR; } k = MAX_SIZE - 1; for( j=1; j <= i-1; j++ ) { k = L[k].cur; // k1 = 1, k2 = 5 } j = L[k].cur; // j = 2 L[k].cur = L[j].cur; Free_SLL(L, j); return OK; } /* 将下标为k的空闲结点回收到备用链表 */ void Free_SLL(StaticLinkList space, int k) { space[k].cur = space[0].cur; space[0].cur = k; } /* 返回L中数据元素个数 */ int ListLength(StaticLinkList L) { int j = 0; int i = L[MAXSIZE-1].cur; while(i) { i = L[i].cur; j++; } return j; }
静态链表优缺点总结
-
优点：
- 在插入和删除操作时，只需要修改游标，不需要移动元素，从而改进了在顺序存储结构中的插入和删除操作需要移动大量元素的缺点。
-
缺点：
- 没有解决连续存储分配（数组）带来的表长难以确定的问题
- 失去了顺序存储结构随机存取的特性
-
总结：
- 总的来说，静态链表其实是为了给没有指针的编程语言设计的一种实现单链表功能的方法
- 尽管我们可以用单链表就不用静态链表了，但这样的思考方式是非常巧妙的，应该理解其思想，以备不时之需
单链表小结，腾讯面试题：
题目：快速找到未知长度单链表的中间结点
- 普通方法：首先遍历一遍单链表以确定单链表的长度L。然后再次从头节点出发循环L/2次找到单链表的中间节点。算法复杂度为：O(L+L/2)=O(3L/2)
#include "stdio.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 typedef int Status; /* Status是函数的类型,其值是函数结果状态代码，如OK等 */ typedef int ElemType; /* ElemType类型根据实际情况而定，这里假设为int */ typedef struct Node { ElemType data; struct Node *next; }Node; typedef struct Node *LinkList; /* 定义LinkList */ Status visit(ElemType c) { printf("%d ",c); return OK; } /* 初始化顺序线性表 */ Status InitList(LinkList *L) { *L=(LinkList)malloc(sizeof(Node)); /* 产生头结点,并使L指向此头结点 */ if(!(*L)) /* 存储分配失败 */ { return ERROR; } (*L)->next=NULL; /* 指针域为空 */ return OK; } /* 初始条件：顺序线性表L已存在。操作结果：返回L中数据元素个数 */ int ListLength(LinkList L) { int i=0; LinkList p=L->next; /* p指向第一个结点 */ while(p) { i++; p=p->next; } return i; } /* 初始条件：顺序线性表L已存在 */ /* 操作结果：依次对L的每个数据元素输出 */ Status ListTraverse(LinkList L) { LinkList p=L->next; while(p) { visit(p->data); p = p->next; } printf("\n"); return OK; } /* 随机产生n个元素的值，建立带表头结点的单链线性表L（尾插法） */ void CreateListTail(LinkList *L, int n) { LinkList p,r; int i; srand(time(0)); /* 初始化随机数种子 */ *L = (LinkList)malloc(sizeof(Node)); /* L为整个线性表 */ r=*L; /* r为指向尾部的结点 */ for (i=0; i < n; i++) { p = (Node *)malloc(sizeof(Node)); /* 生成新结点 */ p->data = rand()%100+1; /* 随机生成100以内的数字 */ r->next=p; /* 将表尾终端结点的指针指向新结点 */ r = p; /* 将当前的新结点定义为表尾终端结点 */ } r->next = NULL; /* 表示当前链表结束 */ // 创建有环链表 //r->next = p; } Status GetMidNode(LinkList L, ElemType *e) { LinkList search, mid; mid = search = L; while (search->next != NULL) { //search移动的速度是 mid 的2倍 if (search->next->next != NULL) { search = search->next->next; mid = mid->next; } else { search = search->next; } } *e = mid->data; return OK; } int main() { LinkList L; Status i; char opp; ElemType e; int find; int tmp; i=InitList(&L); printf("初始化L后：ListLength(L)=%d\n",ListLength(L)); printf("\n1.查看链表 \n2.创建链表（尾插法） \n3.链表长度 \n4.中间结点值 \n0.退出 \n请选择你的操作：\n"); while(opp != '0') { scanf("%c",&opp); switch(opp) { case '1': ListTraverse(L); printf("\n"); break; case '2': CreateListTail(&L,20); printf("整体创建L的元素(尾插法)：\n"); ListTraverse(L); printf("\n"); break; case '3': //clearList(pHead); //清空链表 printf("ListLength(L)=%d \n",ListLength(L)); printf("\n"); break; case '4': //GetNthNodeFromBack(L,find,&e); GetMidNode(L, &e); printf("链表中间结点的值为：%d\n", e); //ListTraverse(L); printf("\n"); break; case '0': exit(0); } } }
-
高级方法：利用快慢指针！
原理：
-
- 设置两个指针*search、*mid都指向单链表的头节点
- 其中* search的移动速度是*mid的2倍
- 当*search指向末尾节点的时候，mid正好就在中间了
- 这也是标尺的思想
Status GetMidNode(LinkList L, ElemType *e) { LinkList search, mid; mid = search = L; while (search->next != NULL) { //search移动的速度是 mid 的2倍 if (search->next->next != NULL) { search = search->next->next; mid = mid->next; } else { search = search->next; } } *e = mid->data; return OK; }
循环链表
将单链表中终端结点的指针端由空指针改为指向头结点，就使整个单链表形成一个环
这种头尾相接的单链表成为单循环链表，简称循环链表
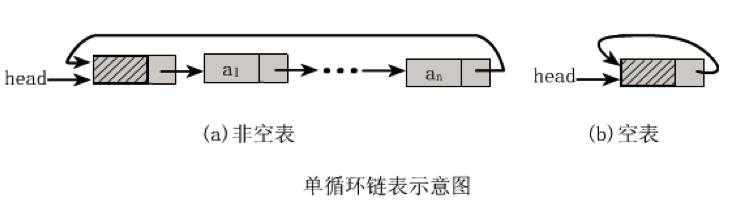
注：
- 这里并不是说循环链表一定要有头结点
- 其实循环链表的单链表的主要差异在于循环的判断空链表的条件上,原来判断head->next是否为null，现在则是head->next是否等于head
循环链表基本操作
循环链表的初始化
typedef struct CLinkList { int data; struct CLinkList *next; }node; /*初始化循环链表*/ void ds_init(node **pNode)//指向指针的指针 { int item; node *temp; node *target; printf("输入结点的值，输入0完成初始化\n"); while(1)//永远为真的循环，通过return结束 { scanf("%d", &item); fflush(stdin); if(item == 0)//输入非零 return; if((*pNode) == NULL)//创建第一个新节点 { /*循环链表中只有一个结点*/ *pNode = (node*)malloc(sizeof(struct CLinkList)); if(!(*pNode)) exit(0); (*pNode)->data = item; (*pNode)->next = *pNode; } else//不知有头结点 { /*找到next指向第一个结点的结点*/ for(target = (*pNode); target->next != (*pNode); target = target->next) ; /*生成一个新的结点*/ temp = (node *)malloc(sizeof(struct CLinkList)); if(!temp) exit(0); temp->data = item;//赋值给新的结点 temp->next = *pNode;//新结点的next指向第一个结点 target->next = temp;//前尾节点指向新节结点 } } }
循环链表的插入
/*链表存储结构的定义*/ typedef struct CLinkList { int data; struct CLinkList *next; }node; /*插入结点*/ /*参数：链表的第一个结点，插入的位置*/ void ds_insert(node **pNode , int i) { node *temp; node *target; node *p; int item; int j = 1; printf("输入要插入结点的值:"); scanf("%d", &item); if(i == 1)//新插入的结点作为第一个结点 { temp = (node *)malloc(sizeof(struct CLinkList)); if(!temp) exit(0); temp->data = item;//直接把数据赋值给新结点 /*寻找到最后一个结点target*/ for(target = (*pNode); target->next != (*pNode); target = target->next) ; temp->next = (*pNode);//将第一个结点赋值给新结点 target->next = temp;//将新结点放到最后一个结点的后面 *pNode = temp;//将新插入的结点当作第一个结点赋值给*pNode } else//新插入的结点不是第一个结点 { target = *pNode;//第一个结点赋值给target for( ; j < (i-1); ++j )//只循环一次 { target = target->next; } // 如果i=3，target变为第二个元素，target指向第三个元素 temp = (node *)malloc(sizeof(struct CLinkList)); if(!temp) exit(0); temp->data = item;//把值赋给新结点 p = target->next;//p作为中转站，先把target->next赋值给p target->next = temp;//再把temp放到target的后面 temp->next = p;//最后把p中原target->next赋值给temp->next } }
循环链表的删除
/*删除结点*/ void ds_delete(node **pNode, int i) { node *target; node *temp; int j = 1; if(i == 1)//如果删除的是第一个结点 { /*找到最后一个结点target*/ for(target = *pNode; target->next != *pNode;target = target->next) ; temp = *pNode;//把第一个结点赋值给*pNode *pNode = (*pNode)->next;//再把*pNode下一个结点(第二个结点)赋值给*pNode target->next = *pNode;//让最后一个结点target指向第二个结点 free(temp);//释放第一个结点 } else//如果删除的结点不是第一个结点 { target = *pNode;//第一个结点赋值给target for( ; j < i-1; ++j)//只循环一次 { target = target->next; } // 如果i=3，target变为第二个元素，target指向第三个元素 temp = target->next;//第三个结点赋值给temp target->next = temp->next;//第四个结点赋值给第二个结点target的next free(temp);//释放第三个结点 } }
循环链表返回结点所在位置
/*返回结点所在位置*/ int ds_search(node *pNode, int elem) { node *target; int i = 1; for(target = pNode; target->data != elem && target->next != pNode; ++i) { target = target->next; } if(target->next == pNode && target->data != elem) /*表中不存在该元素*/ return -1; else return i; }
【约瑟夫（花样自杀）问题】★
41个人排成一个圆圈，由第1个人开始报数，每报数到第3人该人就必须自杀，然后再由下一个重新报数，直到所有人都自杀身亡为止。
#include<stdio.h> #include<stdlib.h> typedef struct node { int data;
struct node *next; }node; node *create(int n) { node *p = NULL, *head; head = (node*)malloc(sizeof(node)); p=head; node *s; int i = 1; if(n != 0) { while (i<=n)//执行41次 { s = (node *)malloc(sizeof(node)); s->data = i++;//先赋值再++，第一个结点为1... p->next = s;//把新节点放到p的后面 p = s; //把新节点结点赋值给p } s->next = head->next;//最后把最后一个结点指向头节点指向的位置（也就是第一个结点） } free(head); return s->next;//返回第一个结点 } int main(){ int n,m=3,i; scanf("%d",&n); node *p = create(n); node *temp;//临时结点 m %= n; //m=3 while (p!=p->next) { for ( i = 1; i < m-1; i++)//执行1次 { p = p->next; } printf("%d->",p->next->data); temp = p->next ; p->next = temp->next ; free(temp); p = p->next ; } printf("%d\n", p->data ); return 0; }
更高挑战
编号为1～N的N个人按顺时针方向围坐一圈，每人持有一个密码（正整数，可以自由输入）。
开始人选一个正整数作为报数上限值M，从第一个人按顺时针方向自1开始顺序报数，报道M时停止报数。
报M的人出列，将他的密码作为新的M值。
从他顺时针方向上的下一个人开始从1报数，如此下去，直至所有人全部出列为止。
#include <stdio.h> #include <stdlib.h> #define MAX_NODE_NUM 100 #define TRUE 1U #define FALSE 0U typedef struct NodeType { int id; int cipher; struct NodeType *next; } NodeType; /* 创建单向循环链表 */ static void CreaList(NodeType **, const int); /* 运行"约瑟夫环"问题 */ static void StatGame(NodeType **, int); /* 打印循环链表 */ static void PrntList(const NodeType *); /* 得到一个结点 */ static NodeType *GetNode(const int, const int); /* 测试链表是否为空, 空为TRUE，非空为FALSE */ static unsigned EmptyList(const NodeType *); int main(void) { int n, m; NodeType *pHead = NULL; while (1) { printf("请输入人数n（最多%d个）: ", MAX_NODE_NUM); scanf("%d", &n); printf("和初始密码m: "); scanf("%d", &m); if (n > MAX_NODE_NUM) { printf("人数太多，请重新输入！\n"); continue; } else break; } CreaList(&pHead, n); printf("\n------------ 循环链表原始打印 -------------\n"); PrntList(pHead); printf("\n-------------删除出队情况打印 -------------\n"); StatGame(&pHead, m); } static void CreaList(NodeType **ppHead, const int n) { int i, iCipher; NodeType *pNew, *pCur; for (i = 1; i <= n; i++) { printf("输入第%d个人的密码: ", i); scanf("%d", &iCipher); pNew = GetNode(i, iCipher); if (*ppHead == NULL) { *ppHead = pCur = pNew; pCur->next = *ppHead; } else { pNew->next = pCur->next; pCur->next = pNew; pCur = pNew; } } printf("完成单向循环链表的创建!\n"); } static void StatGame(NodeType **ppHead, int iCipher) { int iCounter, iFlag = 1; NodeType *pPrv, *pCur, *pDel; pPrv = pCur = *ppHead; /* 将pPrv初始为指向尾结点，为删除作好准备 */ while (pPrv->next != *ppHead) pPrv = pPrv->next; while (iFlag) { for (iCounter = 1; iCounter < iCipher; iCounter++) { pPrv = pCur; pCur = pCur->next; } if (pPrv == pCur) iFlag = 0; pDel = pCur; /* 删除pCur指向的结点，即有人出列 */ pPrv->next = pCur->next; pCur = pCur->next; iCipher = pDel->cipher; printf("第%d个人出列, 密码: %d\n", pDel->id, pDel->cipher); free(pDel); } *ppHead = NULL; getchar(); } static void PrntList(const NodeType *pHead) { const NodeType *pCur = pHead; if (EmptyList(pHead)) return; do { printf("第%d个人, 密码: %d\n", pCur->id, pCur->cipher); pCur = pCur->next; } while (pCur != pHead); getchar(); } static NodeType *GetNode(const int iId, const int iCipher) { NodeType *pNew; pNew = (NodeType *)malloc(sizeof(NodeType)); if(!pNew) { printf("Error, the memory is not enough!\n"); exit(-1); } pNew->id = iId; pNew->cipher = iCipher; pNew->next = NULL; return pNew; } static unsigned EmptyList(const NodeType *pHead) { if(!pHead) { printf("The list is empty!\n"); return TRUE; } return FALSE; }
循环链表的特点
利用循环链表的特点改造现有循环链表，我们不用头指针，而是用指向终端结点的尾指针来表示循环链表
此时查找开始结点和终端结点都很方便
判断是否为空链表：判断rear是否等于rear->next
循环链表的特点:
是无须增加存储量，仅对链接方式稍作改变，即可使得表处理更加方便灵活
一道例题：
题目：实现将两个线性表（a1，a2，…，an）和（b1，b2，…，bm）连接成一个线性表（a1，…，an，b1，…bm）的运算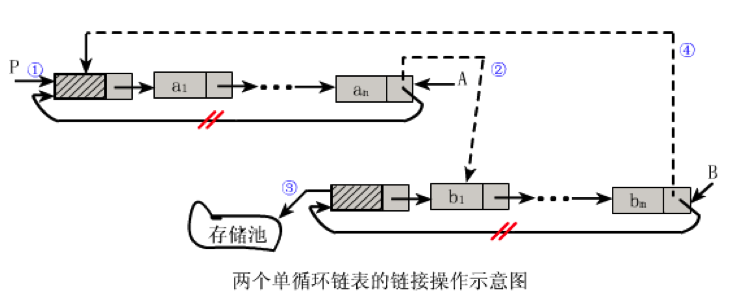
//假设A，B为非空循环链表的尾指针 LinkList Connect(LinkList A,LinkList B) { LinkList p = A->next; //1 保存A表的头结点位置 A->next = B->next->next; //2 B表的开始结点链接到A表尾 free(B->next); //3 释放B表的头结点,初学者容易忘记 B->next = p; return B; //4 返回新循环链表的尾指针 }
判断链表是否有环
有环的定义：链表的尾节点指向了链表中的某个节点
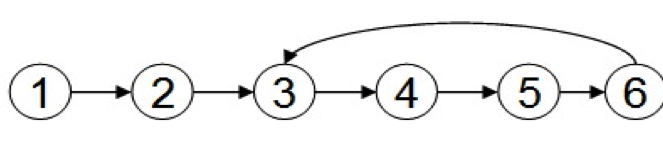
方法一：使用p、q两个指针，p总是向前走，但q每次都从头开始走，对于每个节点，看p走的步数是否和q一样。如图，当p从6走到3时，用了6步，此时若q从head出发，则只需两步就到3，因而步数不等，出现矛盾，存在环。
方法二：使用p、q两个指针，p每次向前走一步，q每次向前走两步，若在某个时候p == q，则存在环
#include "stdio.h" #define OK 1 #define ERROR 0 #define TRUE 1 #define FALSE 0 typedef int Status;/* Status是函数的类型,其值是函数结果状态代码，如OK等 */ typedef int ElemType;/* ElemType类型根据实际情况而定，这里假设为int */ typedef struct Node { ElemType data; struct Node *next; }Node, *LinkList; /* 初始化带头结点的空链表 */ Status InitList(LinkList *L) { *L = (LinkList)malloc(sizeof(Node)); /* 产生头结点,并使L指向此头结点 */ if(!(*L)) /* 存储分配失败 */ return ERROR; (*L)->next=NULL; /* 指针域为空 */ return OK; } /* 初始条件：顺序线性表L已存在。操作结果：返回L中数据元素个数 */ int ListLength(LinkList L) { int i=0; LinkList p=L->next; /* p指向第一个结点 */ while(p) { i++; p=p->next; } return i; } /* 随机产生n个元素的值，建立带表头结点的单链线性表L（头插法） */ void CreateListHead(LinkList *L, int n) { LinkList p; int i; srand(time(0)); /* 初始化随机数种子 */ *L = (LinkList)malloc(sizeof(Node)); (*L)->next = NULL; /* 建立一个带头结点的单链表 */ for (i=0; i < n; i++) { p = (LinkList)malloc(sizeof(Node)); /* 生成新结点 */ p->data = rand()%100+1; /* 随机生成100以内的数字 */ p->next = (*L)->next; (*L)->next = p; /* 插入到表头 */ } } /* 随机产生n个元素的值，建立带表头结点的单链线性表L（尾插法） */ void CreateListTail(LinkList *L, int n) { LinkList p,r; int i; srand(time(0)); /* 初始化随机数种子 */ *L = (LinkList)malloc(sizeof(Node)); /* L为整个线性表 */ r = *L; /* r为指向尾部的结点 */ for (i=0; i < n; i++) { p = (Node *)malloc(sizeof(Node)); /* 生成新结点 */ p->data = rand()%100+1; /* 随机生成100以内的数字 */ r->next=p; /* 将表尾终端结点的指针指向新结点 */ r = p; /* 将当前的新结点定义为表尾终端结点 */ } r->next = (*L)->next->next; } // 比较步数的方法 int HasLoop1(LinkList L) { LinkList cur1 = L; // 定义结点 cur1 int pos1 = 0; // cur1 的步数 while(cur1) { // cur1 结点存在 LinkList cur2 = L; // 定义结点 cur2 int pos2 = 0; // cur2 的步数 while(cur2) { // cur2 结点不为空 if(cur2 == cur1) { // 当cur1与cur2到达相同结点时 if(pos1 == pos2) // 走过的步数一样 break; // 说明没有环 else // 否则 { printf("环的位置在第%d个结点处。\n\n", pos2); return 1; // 有环并返回1 } } cur2 = cur2->next; // 如果没发现环，继续下一个结点 pos2++; // cur2 步数自增 } cur1 = cur1->next; // cur1继续向后一个结点 pos1++; // cur1 步数自增 } return 0; } // 利用快慢指针的方法 int HasLoop2(LinkList L) { int step1 = 1; int step2 = 2; LinkList p = L; LinkList q = L; while (p != NULL && q != NULL && q->next != NULL) { p = p->next; if (q->next != NULL) q = q->next->next; printf("p:%d, q:%d \n", p->data, q->data); if (p == q) return 1; } return 0; } int main() { LinkList L; Status i; char opp; ElemType e; int find; int tmp; i = InitList(&L); printf("初始化L后：ListLength(L)=%d\n",ListLength(L)); printf("\n1.创建有环链表（尾插法） \n2.创建无环链表（头插法） \n3.判断链表是否有环 \n0.退出 \n\n请选择你的操作：\n"); while(opp != '0') { scanf("%c",&opp); switch(opp) { case '1': CreateListTail(&L, 10); printf("成功创建有环L(尾插法)\n"); printf("\n"); break; case '2': CreateListHead(&L, 10); printf("成功创建无环L(头插法)\n"); printf("\n"); break; case '3': printf("方法一: \n\n"); if( HasLoop1(L) ) { printf("结论：链表有环\n\n\n"); } else { printf("结论：链表无环\n\n\n"); } printf("方法二：\n\n"); if( HasLoop2(L) ) { printf("结论：链表有环\n\n\n"); } else { printf("结论：链表无环\n\n\n"); } printf("\n"); break; case '0': exit(0); } } }
魔术师发牌问题
#include <stdio.h> #include <stdlib.h> #define CardNumber 13 typedef struct node { int data; struct node *next; }sqlist, *linklist; linklist CreateLinkList() { linklist head = NULL; linklist s, r; int i; r = head; for(i=1; i <= CardNumber; i++) { s = (linklist)malloc(sizeof(sqlist)); s->data = 0; if(head == NULL) head = s; else r->next = s; r = s; } r->next = head; return head; } // 发牌顺序计算 void Magician(linklist head) { linklist p; int j; int Countnumber = 2; p = head; p->data = 1; //第一张牌放1 while(1) { for(j=0; j < Countnumber; j++) { p = p->next; if(p->data != 0) //该位置有牌的话,则下一个位置 { p->next; j--; } } if(p->data == 0) { p->data = Countnumber; Countnumber ++; if(Countnumber == 14) break; } } } // 销毁工作 void DestoryList(linklist* list)
{
linklist Head, P;
if (*list)
{
Head = *list;
P = Head->next;
while (!P)
{
free(Head);
Head = P;
P = Head->next;
}
}
} int main() { linklist p; int i; p = CreateLinkList(); Magician(p); printf("按如下顺序排列：\n"); for (i=0; i < CardNumber; i++) { printf("黑桃%d ", p->data); p = p->next; } DestoryList(&p); return 0; }
拉丁方阵问题
拉丁方阵是一种n×n的方阵，方阵中恰有n种不同的元素，每种元素恰有n个，并且每种元素在一行和一列中恰好出现一次
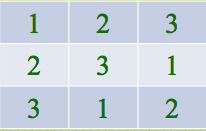请利用循环链表实现一个拉丁方阵！
#include<stdio.h> #define N 6 /*确定N值*/ int main() { int i,j,k,t; printf("The possble Latin Squares of order %d are:\n",N); for(j=0;j<N;j++) /*构造N个不同的拉丁方阵*/ { for(i=0;i<N;i++) { t=(i+j)%N; /*确定该拉丁方阵第i 行的第一个元素的值*/ for(k=0;k<N;k++) /*按照环的形式输出该行中的各个元素*/ printf("%d",(k+t)%N+1); printf("\n"); } printf("\n"); } }
双向链表
双向链表节点结构
typedef struct DualNode { ElemType data; struct DualNode *prior; //前驱结点 struct DualNode *next; //后继结点 } DualNode, *DuLinkList;
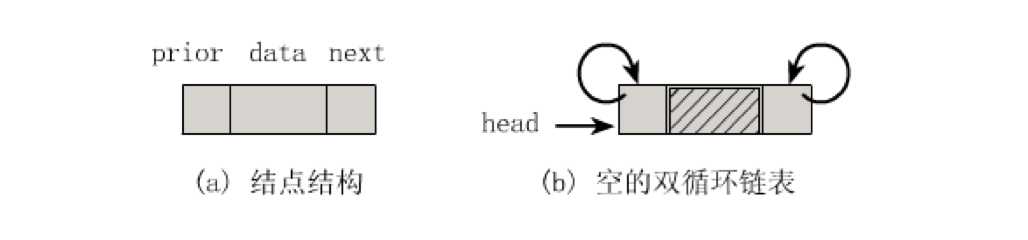
由于这是双向链表，那么对于链表中的某一个结点p，它的后继结点的前驱结点是它本身
插入操作
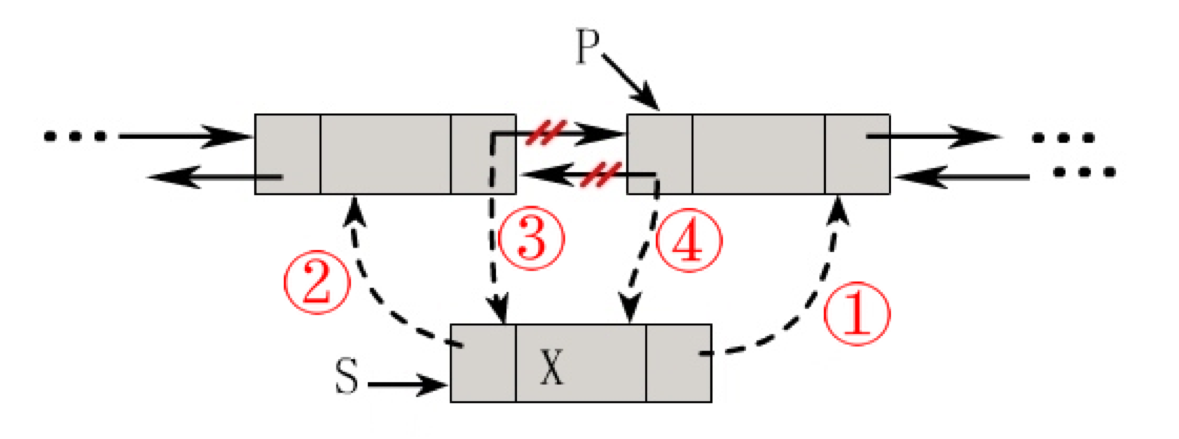
s->next = p; s->prior = p->prior; p->prior->next = s; p->prior = s;
删除操作
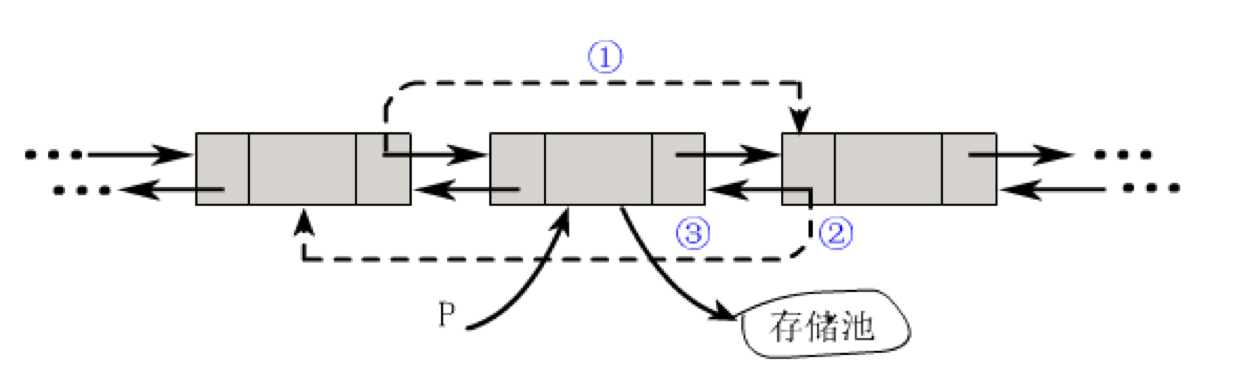
p->prior->next = p->next; p->next->prior = p->prior; free(p);
双向链表相对于单链表来说，是要更复杂一点。
每个结点多了一个prior指针，对于插入和删除操作的顺序大家要格外小心。
不过，双向链表可以有效提高算法的时间性能，说白了就是用空间来换取时间。
