数据结构与算法（二）：时间复杂度和空间复杂度

算法效率的度量方法:

  1. 算法采用的策略，方案
  2. 编译产生的代码质量
  3. 问题的输入规模
  4. 机器执行指令的速度

　　由此可见，抛开这些与计算机硬件、软件有关的因素，一个程序的运行时间依赖于算法的好坏和问题的输入规模 

　　我们研究算法的复杂度，侧重的是研究算法随着输入规模扩大增长量的一个抽象，而不是精确的定位需要执行多少次

　　我们不关心语言、环境等，只关心它所实现的算法。
　　我们在分析一个算法的运行时间时，重要的是把基本操作的数量和输入模式关联起来

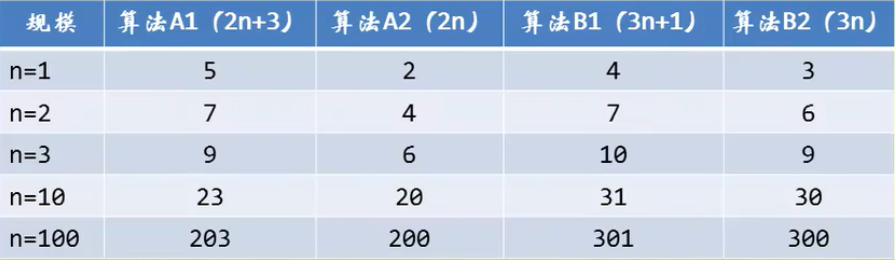
　　 当n=1是，A算法不如B算法，随着n的增长，A算法反超B算法，总体来说A比B算法更优秀

　函数的渐近增长：给定两个函数f(n)和g(n)，如果存在一个整数N，使得对于所有的n>N,f(n)总是比g(n)大，那么我们说f(n)的增长渐近快于g(n)

 

算法时间复杂度

 

定义：在进行算法分析时，语句总的执行次数T(n)是关于问题规模n的函数，进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度，也就是算法时间度量，记作T(n) = O(f(n))。它表示随问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称作算法的渐近时间复杂度，简称时间复杂度，其中f(n)是问题规模n的某个函数。（关键点：执行次数==时间）

 

　　

如何分析一个算法的时间复杂度

  • 用常数1取代运行时间中的所有加法常数
  • 在修改后的运行次数函数中，只会保留最高阶
  • 如果最高阶项存在且不是1，则去除与这个项相乘的常数
  • 得到的最后结果就是大O阶

常数阶：

int sum=0,n=100;
printf("Hello World!");
printf("Hello World!");
printf("Hello World!");
printf("Hello World!");
printf("Hello World!");
printf("Hello World!");
printf("Hello World!");
printf("Hello World!");
sum = (1+n)*n/2;

 

 

时间复杂度不是O(8)，而是O(1)

 

线性阶：一般含有非嵌套循环涉及线性阶，线性阶就是随着问题规模n的扩大，对应的计算次数呈直线增长

int i,sum=0,n=100;
for(i=1;i<=n;i++)
{    
    sum=sum+i;
}

 

时间复杂度为O(n)

 

平方阶：N次嵌套循环

int i,j,n=100;
for(i=1;i<=n;i++)
{    for(j=0;j<n;j++)
    {
        printf("Hello，World");
    }
}

 

 时间复杂度为O(nN)

 

 对数阶：

int i=1,n=100;
while(i<n)
{
    i=i*2;      
}

 

 每次i*2就距离n更近一步，所以由2x = n得到x = log2n,所以这个循环的时间复杂度为O(logn)

 

函数调用的时间复杂度分析

1 int i,j; 2 for(i=0;i<n;i++){ 3 function(i); 4 ) 5 6 void function(int count){ 7 printf("%d",count); 8 }// function函数的时间复杂度是O(1),所以整体的时间复杂度就是循环的次数O(n)

1 int i,j; 2 for(i=0;i<n;i++){ 3 function(i); 4 ) 5 6 void function(int count){ 7 int j; 8 for(j=count;j<n;j++){ 9 printf("%d",j); 10 } 11 }//function内部的循环次数随着count的增加(接近n)而减少，所以根据游戏攻略算法的时间复杂度为O(n2)

思考：

n++;//   　　　　　　　　　　　　　　1
function(n);//　　　　　　　　　　　n2
for(i=0;i<n;i++)//　　　　　　　　 n2
{
    function(n);
}
for(i=0;i<n;i++)//　　　　　　　　 n2
{
    for(j=i;j<n;j++)
    {
        printf("%d\n",j);
    }
}

 

答案：上述代码的时间复杂度为O(n^2)

 

常见的时间复杂度

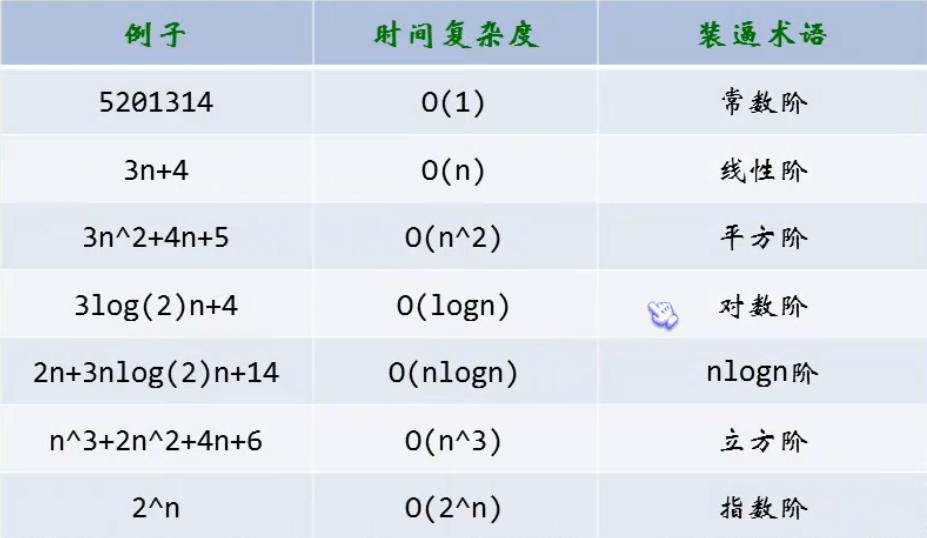
 耗费的时间从小到大：

O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)

 

最坏情况和平均情况

  • 平均运行时间是期望的运行时间
  • 最坏运行时间是一种保证。在应用中，这是一种最重要的需求，通常除非特别指定，我们提到的运行时间都是指最坏情况的运行时间

 

算法的空间复杂度 

首先我们要明白，我们在写代码时，完全可以用空间来换取时间。

 

举个例子：判断某一年是否为闰年

　　我们可以实现要给算法，每给一个年份，都会通过算法计算得到是否是闰年的结果。
　　另一种算法就是，建立一个数组，将所有年份按下标的数字对应，如果是闰年，则此数组元素对应的值为1，否则为0.

　　解析：对比两个算法，第一种算法很明显节约空间，但是每一次查询都需要进行运算，而第二种算法，虽然在内存中存了几千个数组，但是每次查询只需要一次索引即可。

这就是典型的空间换时间。

 

 　　算法的空间复杂度通过计算算法所需的存储空间实现，算法的空间复杂度的计算公式为：S(n)=O(f(n)),其中，n为问题的规模，F(n)为语句关于n所存储空间的函数。

　　通常，我们都是用“时间复杂度”来指运行时间的需求，是用“空间复杂度”指空间需求

　　当直接要求我们求“复杂度”时，通常是指时间复杂度

 

 

 显然，对时间复杂度的追求更属于算法的潮流QAQ

 
posted @ 2020-04-13 22:54  kyrie_wx  阅读(599)  评论(0)  编辑  收藏  举报