最全对称加密----流密码总结到位
它是以最小单位比特作为一次加密、解密的操作元素,利用加密算法进行加密与解密。流密码的基本思想是利用密钥 k 产生一个密钥流 z ,并利用相应的规则对明文串 x进行加密,所得到的密文为: y 。
而流密码与所谓的分组密码最大的差距除了对于明文的处理方式不同以外,还有其加密器中是否含有记忆元件,流密码的加密器中存在记忆元件,而分组密码不存在,也正是由于这个记忆元件,我们可以进一步将流密码分为同步流密码和自同步流密码。
同步流密码:
是不是听起来有点复杂,但其实它取决于加密器中记忆元件的存储状态,独立于明文字符的叫做同步流密码,否则叫做自同步流密码, 但其实对于自同步流密码来说,它的密钥流的产生与输入的明文有关, 所以在理论上我们很难能够去分析清楚。而目前,我们在流密码方面的所有科研成果绝大多数都是关于同步流密码的。
同步流密码的加密过程都与明文无关,故我们得到的密文也与明文直接联系。所以,通常情况下我们将同步流密码的加密器分成密钥流产生器和加密变换器两个部分。在下图所表示的就是流密码的加密和解密流程。
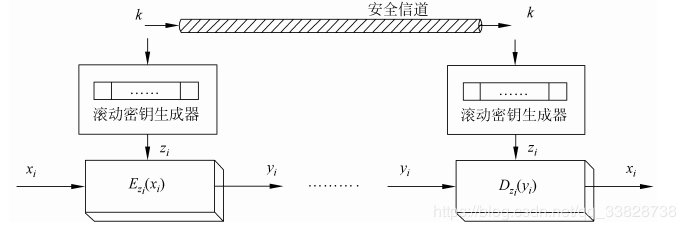
我们输入明文x,利用密钥流生成器生成的密钥z,利用加密算法E对明文x进行加密。可以得到密文y。
反过来说,当我们已知密文y时,利用密钥z和解密算法D解析密文y,就可以得到明文x。
同步流密码的加密算法E可以是各种各样的,但是我们必须保证变换是可逆的(也就是说通过明文利用加密算法可以得到密文,反过来利用密文和解密算法就可以得到明文)。
实际使用的数字保密通信系统一般都是二元系统,所以说,在有限域 GF(2)上讨论的二元加法流密码是目前最为常用的流密码体制。

其实通过这两幅图我们可以对比出来,在二元域中,二元加法流密码就是将我们的加密算法换成了所谓的二元域上的加法。(相信学计算机的我们一定对这个不陌生吧!hhhh~)
线性反馈移位寄存器LFSR:
线性反馈移位寄存器(LFSR):通常由移位寄存器和异或门逻辑组成。其主要应用在:伪随机数,伪噪声序列,计数器,BIST,数据的加密和CRC校验等。在这里我们主要说LFSR在密码学中的应用,尤其是在流密码中,线性反馈移位寄存器是组成密钥流生成器的一个重要部分。
GF(2 )上一个 n 级反馈移位寄存器由 n 个二元存储器与一个反馈函数 f ( a1 , a2 ,…, an )组成。话不多说,我们直接看图。
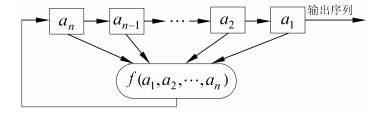
图中可以看到每一存储器称为移位寄存器的一级,在任一时刻,这些级的内容构成该反馈移位寄存器的状态,每一状态对应于GF(2)上的一个 n 维向量,共有2n种可能的状态。每一时刻的状态可用 n 长序列 a1 , a2 ,…, an表示, 其中 ai 是第 i 级存储器的内容。
初始状态由用户确定,当第 i 个移位时钟脉冲到来时,每一级存储器 ai 都将其内容向下一级 ai - 1 传递, 并根据寄存器此时的状态 a1 , a2 , …, an 计算 f ( a1 , a2 , …, an ) ,作为下一时刻的 an。
反馈函数 f ( a1 , a2 , …, an ) 是 n 元布尔函 , 即 n 个变元 a1 , a2 ,…, an 可以独立地取 0 和 1 这两个可能的值, 函数中的运算有逻辑 与、逻辑或、逻辑补等运算,最后的函数值也为 0 或 1。
线性反馈移位寄存器输出序列的性质完全由其反馈函数决定。 n 级线性反馈移位寄存器最多有 2的n次方个不同的状态。若其初始状态为 0,则其状态恒为 0。若其初始状态非 0,则其后边的状态也不会为 0。因此 n 级线性反馈移位寄存器的状态周期小于等于 2的n次方- 1。其输出序列的周期与状态周期相等, 也小于等于 2的n次方- 1。只要选择合适的反馈函数便可使 序列的周期达到最大值 2的n次方- 1,周期达到最大值的序列称为 m 序列。
m序列:
m序列也就是最长线性移位寄存器序列的简称,是由线性反馈的移存器产生的周期最长的序列,也是一种伪随机序列。
什么是伪随机序列?
伪随机序列也就是,即使截获其中一段,也无法推测后面是什么。如果说密钥流是周期的, 要完全做到随机性是困难的。严格地说, 这样的序列不可能做到随机, 只能要求截获比周期短的一段密钥流时不会泄露更多信息, 这样的序列称为伪随机序列。
m序列的性质:
均衡性:
由m序列的一个周期中,一般情况下,0和1的数目基本相等或者1的数目比0的数目多一个。
例如0111101101001100000111001010101看出:总共有16个1和15个0。
游程分布:
m序列中取值相同的那些相继的元素合称为一个“游程”。游程中元素的个数称为游程长度。
n级的m序列中,总共有2n-1个游程,其中长度为1的游程占总游程数的1/2,长度为2的游程占总游程数的1/4,长度为k的游程占总游程数的2k。且长度为k的游程中,连0与连1的游程数各占一半。
如序列0111101101001100000111001010101中,游程总数为18-1=17,此序列各种长度的游程分布如下:
长度为1的游程数目为10,其中5个1游程和5个0游程;
长度为2的游程数目为4,2个11游程,2个00游程;
长度为3的连1游程数目为1;
长度为4的连0游程数目为1;
长度为5的连1游程数目为1。
移位相加特性
一个m序列m1,m序列经任意延迟移位产生的另一序列m2,将m1与m2进行模2加运算,所得到的序列仍是m1的某次延迟移位序列 m3,并且m3等于m1与m2 异或。
相关特性
我们可以根据移位相加特性来验证m序列的自相关特性。因为移位相加后得到的还是m序列,因此0的个数比1的个数少1。
Golomb 公设:
由m序列的性质,我们可以验证Golomb 对伪随机周期序列提出了应满足的如下3 个随机性公设,具体如下:
① 在序列的一个周期内, 0 与 1 的个数相差至多为 1。
公设①说明{ ai}中 0 与 1 出现的概率基本上相同
② 在序列的一个周期内,长为 i 的游程占游程总数的2的n次方分之1 ( i = 1, 2 ,… ),且在等长的游程中 0 的游程个数和 1 的游程个数相等。
公设②说明 0 与 1 在序列中每一位置 上出现的概率相同。
③ 异相自相关函数是一个常数。
③ 异相自相关函数是一个常数。
公设③意味着通过对序列与其平移后的序列做比较, 不能给出其他任何信息。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号