【斜率优化】玩具装箱

玩具装箱

题目描述

\(P\)教授要去看奥运，但是他舍不下他的玩具，于是他决定把所有的玩具运到北京。他使用自己的压缩器进行压缩，其可以将任意物品变成一堆，再放到一种特殊的一维容器中。\(P\)教授有编号为 \(1⋯N \)的 \(N\) 件玩具，第 \(i\)件玩具经过压缩后变成一维长度为 \(Ci\) .为了方便整理，\(P\)教授要求在一个一维容器中的玩具编号是连续的。同时如果一个一维容器中有多个玩具，那么两件玩具之间要加入一个单位长度的填充物，形式地说如果将第 \(i \)件玩具到第 \(j \)个玩具放到一个容器中，那么容器的长度将为 \(x=j-i+\sum\limits_{k=i}^{j} C_k\)制作容器的费用与容器的长度有关，根据教授研究，如果容器长度为 \(x\),其制作费用为 \((X-L)^2\).其中\( L\) 是一个常量。\(P\)教授不关心容器的数目，他可以制作出任意长度的容器，甚至超过 \(L\)。但他希望费用最小.

输入输出格式

输入格式：

第一行输入两个整数\(N\)，\(L\).接下来\(N\)行输入\(Ci\).\(1<=N<=50000,1<=L,Ci<=10^7\)

输出格式：

输出最小费用

输入样例

5 4
3
4
2
1
4

输出样例

1

首先，这道题有一个明显的\(DP\)方程：

\(f[i]=min{f[j]+(i-j-1+sum[i]-sum[j]-L)^2}\)

显然\(TLE\)

考虑这个方程

设\(A[i]=i+sum[i]，B[i]=i+sum[i]+1+L\)，则原方程为\(f[i]=f[j]+(A[i]-B[j])^2=f[j]+A[i]^2-2*A[i]*B[j]+B[j]^2\)

\(f[i]-A[i]^2+2*A[i]*B[j]=f[j]+B[j]\)

设\(B[j]=x，f[j]+B[j]=y\)

则\(a*A[i]*x+f[i]-A[i]^2=y\)

我们要让\(f[i]-A[i]^2\)最小。这个方程的斜率一定，则我们要找一个点\((x,y)\)使得这个方程的截距最小。

我们考虑一些已经有的点

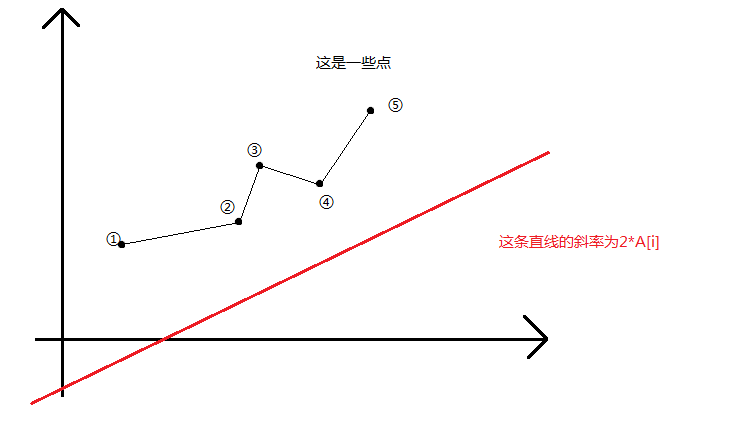
这条直线不断向上移动，最先碰触到的点必定是最优的点。显然，③号点永远不会被用到，那么我们就可以抛弃他。显然，我们最后得到的会是一个下凸包。

考虑怎样加点？

观察图发现，能存在在图上的相邻点之间的连线的斜率越来越大。因此，我们只需要判断当前点与队尾的点的连线斜率是否大于队尾的点与前一个点的连线斜率即可。

如何退队？

当该点与后一个点的连线斜率小于\(2*A[i]\)时，就不会被用到了，于是我们可以鸟尽弓藏扔掉它。

这是我做过的斜率优化的第一道题。斜率优化大体思路就是用函数思想搞一搞，看答案是否单调，然后搞个队列维护一下。

代码

#include<iostream>
#include<cstdio>
using namespace std;
long long n,c[50005],l,a[50005],b[50005],h=1,t=1,f[50005],q[50005];
long long read() {
    long long x=0;int f=0;char c=getchar();
    while(c<'0'||c>'9')f|=c=='-',c=getchar();
    while(c>='0'&&c<='9')x=(x<<3)+(x<<1)+(c^48),c=getchar();
    return f?-x:x;
}
long long count(int x,int y) {//计算斜率
    return ((f[x]+b[x]*b[x])-(f[y]+b[y]*b[y]))/(b[x]-b[y]);
}
int main() {
    n=read(),l=read();
    for(int i=1;i<=n;++i) c[i]=read()+c[i-1];//前缀和 
    for(int i=1;i<=n;++i) f[i]=1e18,a[i]=c[i]+i,b[i]=c[i]+i+1+l,q[i]=0;//预处理 
    b[0]=1+l;
    for(int i=1;i<=n;++i) {
        while(h<t&&count(q[h],q[h+1])<=2*a[i]) h++;//退队
        f[i]=f[q[h]]+(a[i]-b[q[h]])*(a[i]-b[q[h]]);
        while(h<t&&count(q[t-1],q[t])>=count(q[t],i)) t--;
        q[++t]=i;//入队
    }
    printf("%lld",f[n]);
    return 0;
}

感谢\(ZAY\)的讲解
欢迎指正评论O(∩_∩)O~~