KMP

\(KMP\)

\(KMP\)算法是用于字符串比配问题的一种高效算法。

思路如下：

考虑如果我们自己做字符串匹配，当两个字符串不匹配时，我们一般不会从头开始，而是找有没有一个前缀和当前匹配过的字符串后缀相同，这样我们就不用从头开始，节省了时间。

\(KMP​\)的思路就是这样。假如有两个字符串\(a​\)和\(b​\)，用\(a​\)匹配\(b​\)。那我们先用\(a​\)自己匹配自己。这里用一个\(next[~]​\)记录当匹配到第\(i​\)个字符时，与当前匹配过的字符串的后缀相同的最大前缀的后一个位置的序号。

如下图：

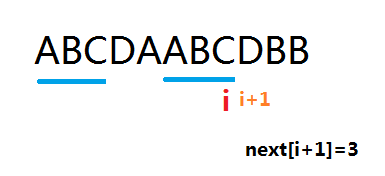
更新\(next\)数组时，采取“向前更新”原则，也就是说，用当前这个更新下一个。假如当前匹配到一段与后缀相同的最大前缀，那么下一个点如果没有匹配上，就应该从那个前缀的后一个位子开始匹配。

\(next\)数组的意思通俗点讲，就是当当前匹配的字符失配之后，我应该从前面的哪个字符重新开始匹配更节约时间。那么我们用当前的结果去更新下一个的结果，就完全可以理解了：当前的\(next\)数组已经有了，也就是说以这个字符为终点的字符串中，最大且相等的前缀和后缀我都知道了，那么下一个字符一旦失配，我就从已经找到的前缀的下一个字符开始匹配就好了。

强调一下，\(next\)数组是自己和自己匹配产生的，但匹配的原则与两个字符串相互匹配道理相同，思路都是一样的。

这个\(KMP\)我理解了好久嘤嘤嘤

\(Code\)

\(KMP\)模板

#include<iostream>
#include<cstring>
#include<cstdio>
using namespace std;
char a[1000006],b[1000006];
int nxt[1000006],j;
int main(){
	cin>>a>>b;
	int n=strlen(a),m=strlen(b);
	for(int i=1;i<m;++i){//自己和自己匹配，处理处next数组
		while(j&&b[i]!=b[j]) j=nxt[j];
		j+=(b[i]==b[j]),nxt[i+1]=j;
	}
	j=0;
	for(int i=0;i<n;++i){
		while(j&&a[i]!=b[j]) j=nxt[j];
		j+=a[i]==b[j];
		if(j==m) printf("%d\n",i-m+2);//题目需要
	}
	for(int i=1;i<=m;++i) printf("%d ",nxt[i]);
	return 0;
}