「题解」异或
披着位运算皮的莫队（114514）
原题出处：没找到
原题链接：题库暂未公开
「我的做题历程」：
step1：观察题面
题面如下图。
看到这个「区间询问」，我的脑子里闪过了「树状数组」和「前缀和」。然而这两种做法都有都有超时的风险。（算法：未知）
step2：思考解法
我并没有想到怎么用树状数组做，于是开始想前缀和 + 暴力。
这道题最主要的部分是这个「区间 \([l, r]\) 中所有出现且出现了偶数次的整数」怎么求。可是，在正常的题目里，我们求的往往是一个区间中出现奇数次的数的异或和。
于是，我有了一个大胆的想法。用这段区间的异或和，异或上这段区间所有元素与整数的交集（即异或上这段区间里所有不同的元素）。譬如 \(3, 4, 3, 5, 5\)，其所有元素与整数的交集是 \(3, 4, 5\)。这就相当于让原本出现奇数次的元素「出现」偶数次，让原本出现偶数次的元素「出现」奇数次。通过这样的转换，就可以求到这段区间的所有出现且出现了偶数次的整数的异或和。
这种解法有两个难点：
- 怎么求任意区间的异或和？
- 怎么求这段区间所有元素与整数的交集？
对于第一个难点，使用暴力是妥妥 TLE。我们可以使用异或前缀和，其原理与前缀和相似。
对于第二个难点，思来想去发现我只会 set。
但是我害怕超时（望向卡常大佬）。
。。。OK，行。
50 tps 代码：
#pragma GCC optimize("Ofast,no-stack-protector")
#pragma GCC target("sse,sse2,sse3,ssse3,sse4,popcnt,abm,mmx,avx,tune=native")
#define R register
#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 3e5 + 5;
int n, m, l, r;
ll a[N], pre[N], sum;
set<ll> s;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%lld", &a[i]);
pre[i] = pre[i - 1] ^ a[i];
}
sum = pre[n];
scanf("%d", &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &l, &r);
ll t = pre[r] ^ pre[l - 1];
s.clear();
for (int j = l; j <= r; j++) {
s.insert(a[j]);
}
ll ans = 0;
set<ll>:: iterator it = s.begin();
for (it; it != s.end(); it++) {
ans ^= *(it);
}
printf("%lld\n", ans ^ t);
}
return 0;
}
尽管有了 O2O3的加持，最后还是 50TLE。。。（烦的嘞）
事实上，这种做法是 \(O(mn)\)，而 \(n, m\) 都能取到 3e5（QAQ），妥妥的超时。。
抓破脑壳也不知道怎么再优化了（再次望向大佬）
（烦的嘞）
幸好 yzq 之前教过我莫队（heihei），不然这道题彻底完蛋。
使用莫队前先估下时间复杂度。
好的，行。（算法：莫队）
于是我顿悟了。
它给了所有区间，而异或和本就可以一步步拓展，\(n, m\) 给的刚好能过莫队——那为什么不莫队。。。
正经思考：
既然要求出现偶数次的元素，那我首先就会想到 \(cnt\) 数组计数，但是这个 \(a_i\) 有点大，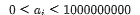
。所以，我们需要对 \(a\) 数组进行离散化，将其变为 \(0 \lt a_i \le 300000\) 的数组，这样就能用桶计数。
之后，就是直接使用莫队求解。（莫队学习传送门：莫队）
众所周知，莫队的核心是从 \([l, r]\) 的答案扩展到与其相邻的区间的答案的过程。（也许雾）
那么，怎么对区间进行拓展？
让我们再对「区间 \([l, r]\) 中所有出现且出现了偶数次的整数」换一种理解方式 =>「区间 \([l, r]\) 中所有出现且出现次数减一为奇数的整数」。
那么对于每一个新添进来的数：如果它在区间中只出现了一次，我们就不管它；如果它出现了一次以上，我们才把它和答案异或，这样就等价于「让这个元素的出现次数减一」。
相似地，对于每一个新删去进来的数：如果它原本在区间中只出现了一次，我们就不管它；如果它原本出现了一次以上，我们把它和答案异或（利用了异或的自反性）。
step3：完成代码
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 3e5 + 5;
int n, m, cnt[N], l, r;
ll a[N], b[N], c[N], ans[N], sum, block = 2583;// 听说常数分块更快？？
struct que {
int l, r, id;
} Q[N];
int get_block(int x){
return x / block + 1;
}
bool cmp(que x, que y) { // 莫队变得正常起来
int a = get_block(x.l);
int b = get_block(y.l);
if (a != b) {
return a < b;
}
return x.r < y.r;
}
void add(int x, ll &res) {
cnt[a[x]]++;
if (cnt[a[x]] != 1) {
res ^= c[x];
}
return;
}
void del(int x, ll &res) {
if (cnt[a[x]] != 1) {
res ^= c[x];
}
cnt[a[x]]--;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%lld", &a[i]);
b[i] = a[i];
c[i] = a[i];
}
sort(b + 1, b + n + 1);
ll len = unique(b + 1, b + n + 1) - b - 1ll;
for (int i = 1; i <= n; i++) {
a[i] = lower_bound(b + 1, b + len + 1, a[i]) - b;
}
scanf("%d", &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &Q[i].l, &Q[i].r);
Q[i].id = i;
}
sort(Q + 1, Q + m + 1, cmp);
for (int i = 1; i <= m; i++){
int id = Q[i].id;
while(r < Q[i].r) add(++r, sum);
while(r > Q[i].r) del(r--, sum);
while(l < Q[i].l) del(l++, sum);
while(l > Q[i].l) add(--l, sum);
ans[id] = sum;
// printf("%d %d %d\n", l, r, ans[Q[i].id]);
}
for (int i = 1; i <= m; i++) {
printf("%lld\n", ans[i]);
}
return 0;
}
（异或出一个 Accepted (heihei)）
让我们来解决 『异或』 叭~
Bye bye!!1 👋👋
