「题解」相框
这相框怕不是用来装我的遗像
(尝试不写缩进.ing)
原题出处:福建集训 2011
原题链接:link
「我的做题历程」:
step1:观察题面
「T 君不满足于焊接奇形怪状的作品,强烈的破坏欲驱使他拆掉这个作品,然后将之焊接成规整的形状。这会儿,T 君正要把这个怪物改造成一个环形,当作自己的相框。」——(变图为简单环)
「原有的作品可能不是连通的。」——(联通块可能不止一个)
「若不与任何焊点相连,则将这一端标号为 \(0\)。」——(可能有孤点)
「烧熔一个焊点:使得连接在焊点上的某些导线相分离或保持相连(可以理解为:把焊点上的导线划分为若干个类,相同类中的导线相连,不同类之间的导线相离)」——(允许拆点)。
注释:这里的「拆(熔)点」指什么?
下图即是一个熔点操作。
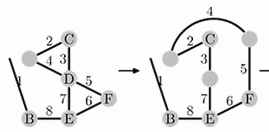
「某些焊点甚至没有任何导线与之相连,由于 T 君只关心导线,因此这些焊点可以不被考虑。」——(边用完后没连接上的的点不必考虑)。
一句话题意:给你一张图(可能是不连通的),允许更换端点或拆点,求最少操作多少步,使得原图变成一个简单环(不必联通所有的点,但要用上所有的边)。(不知道简单环的同学这边请 → 图论相关概念)
step2:思考解法
首先,我们需要承认:无向简单环上的所有点的入度和出度都等于 \(2\)。
然后,从简单想起(有且仅有一个联通块时)——
若要满足题意,则对于图上任一点 \(u\),都有 \(d^-(u) = 2\),所以我们要熔掉所有度数大于 \(2\) 的点。偶点便熔成若干入度为 \(2\) 的点,奇点便熔成若干入度为 \(2\) 的点 + 一个孤立点。
熔完后,对于图上任一点 \(u\),一定有 \(d^-(u) \le 2\),即此时图中一定仅存在链。这个时候要把他们变成简单环就简单的多了,只需首尾相连即可。
接着推广(有多个联通块时)——
先将所有联通块按上述方式拆解成若干条链,再把所有链连起来即可。值得注意的是,熔解过程中可能出现某一点 \(u\),其 \(d^-(u) \equiv 1 \pmod 2\) (即入度为奇数的点,指上文的奇点),其熔解后多出来的孤立点需要和另一入度为 \(1\) 的点熔合;而对于熔合时出现的入度为 \(2\) 的点,。
还有 原本就孤立的点(自环或无边) 需要处理。当其他连通块拆解后仅剩链,没有多余的点来连接,而此时又有多余的边时,我们需要新建一个点与其连接。(因为题目只要求边连完,多加几个点也是没有问题的)
step3:完成代码
整合前面的分析,我们可以得出:ans = 奇点数除以二 + 偶点操作总数 + 入度大于 \(2\) 的点数。
代码(抵制学术不端行为,拒绝 Ctrl + C):
#include <cstdio>
#include <algorithm>
using namespace std;
const int N = 1e6 + 5, M = 2e5 + 5;
int n, m, a, b, d[N], tot, head[N], out[N], id[N], cnt1[N], cnt2[N], cnt;
struct Edge {
int to, next;
} e[M << 1];
void add(int u, int v) {
e[++tot].next = head[u], e[tot].to = v, head[u] = tot;
return;
}
void dfs(int node) { // 也可用并查集
id[node] = cnt; // 区分不同的连通块
for (int i = head[node]; i; i = e[i].next) {
int y = e[i].to;
if (!id[y]) {
dfs(y);
}
}
return;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
if (!a) a = ++n; // 为孤立的点建点配对
if (!b) b = ++n;
d[a]++;
d[b]++;
add(a, b);
add(b, a);
}
if (!n) { // 没有点就把所有边连起来
printf("%d", m);
} else {
for (int i = 1; i <= n; i++) {
if (!id[i] && d[i]) {
cnt++;
dfs(i); // 染出不同的联通块,也可用并查集
}
}
int odd = 0, even = 0, over = 0;
// 分别代表:奇点数,偶点数,入度超过 2 的点数
for (int i = 1; i <= n; i++) {
if (!d[i]) {
continue;
}
if (d[i] & 1) {
cnt1[id[i]] = true; // 该块有奇点
odd++; // 统计奇点
}
if (d[i] > 2) {
cnt2[id[i]] = true; // 该块有入度大于二的点
over++; // 统计入度大于二的点
}
}
for (int i = 1; i <= cnt; i++) {
if (!cnt1[i]) {
if (!cnt2[i]) { // 该联通块仅有入度为 2 的点(是个环)
even += 2; // 拆环 + 熔合
} else {
even++; // 熔合
}
}
}
int ans = (odd >> 1) + even + over;
// 奇点两两融合,偶点可能熔合或拆环,入度大于二的点必须熔掉
printf("%d", ans);
}
return 0;
}
(相框里除了某君的遗像外还有 Accepted (heihei))
让我们来解决 『相框』 叭~
Bye bye!!1 👋👋


