关于『数据结构』：图论
序言
拥抱大只图论。
诸位怎么都如此能肝，md 就我图论还没写完。
(投放My blogs csdn & 博客园😃。)
导览
一、图的基本概念
（一）什么是图（已更）
（二）图的存储（已更）
（三）图的遍历（已更）
二、最短路
（一）Floyd（已更）
（二）Dijkstra（已更）
（三）Bellman-Ford（已更）
（四）SPFA（已更）
三、最小生成树
（一）Prim（已更）
（二）Kruskal（已更）
四、拓扑排序（咕咕）
一、图的基本概念
（一）什么是图（graph）？
举个🌰（栗子）：
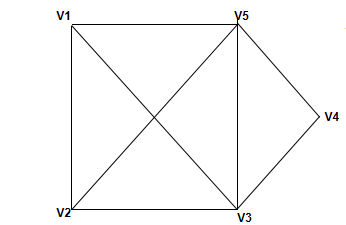
图是由若干给定的顶点（例如 \(V1, V2\)）及连接两顶点的边（例如 \((V1, V2),(V4, V5)\)）所构成的图形。
这种图形通常用来描述某些具体事物之间的某种特定关系。顶点用于代表事物，连接两顶点的边则用于表示具体事物间的关系。
若一张图的边数远小于其点数的平方，那么它是一张稀疏图 (sparse graph)。
若一张图的边数接近其点数的平方，那么它是一张稠密图 (dense graph)。
若一张图的每条边都被赋予一个数作为该边的 权，则称这张图为赋权图。如果这些权都是正实数，就称其为正权图。
若图中存在两条边，则它们被称作一组重边(multiple edge)。
如果一张图中有自环或重边，则称它为多重图 (multigraph)。
Tips：在题目中，如果没有特殊说明，是可以存在自环和重边的，在做题时需特殊考虑。
若一张图中没有自环和重边，它被称为简单图 (simple graph)。
边集为空的图称为无边图 (edgeless graph)、空图 (empty graph) 或零图 (null graph)，\(n\) 阶无边图记作 \(\overline K_n\) 或 \(N_k\)。
图的点数也被称作图的阶 (order)。
📚 更严谨的定义
图 (graph) 是一个有序二元组 \(G = (V, E)\) 。其中 \(V\) 是非空集，称为点集 (vertex set)，对于 \(V\) 中的每个元素，我们称其为顶点 (vertex) ，简称点；\(E\) 为 \(V\) 各结点之间边的集合，称为边集 (edge set)，\(E\) 的元素都是二元组，用 \((x,y)\) 表示，其中 \(x,y \in V\)。
常用 \(G = (V, E)\) 表示图。当 \(V,E\) 都是有限集合时，称 \(G\) 为有限图；当 \(V\) 或 \(E\) 是无限集合时，称 \(G\) 为无限图。
1. 图的种类
图有多种，包括无向图（undirected graph），有向图（directed graph），混合图（mixed graph），带权图（weighted graph）等（还有很多乱七八糟丰富多彩的图，有兴趣可自行搜索）。
（1）有向图
Ⅰ. 定义
每条边都有方向的图称为有向图。
Ⅱ. 术语
-
有向边：有向图中的边被称为有向边（directed edge)），又称为弧（arc），在不引起混淆的情况下也可以称作边（edge）；起点称为弧头（tail），终点称为弧尾（head）。在有向图中，与一个顶点相关联的边有出边和入边之分。
❔ 为什么起点是 tail，终点是 head？
边通常用箭头表示，而箭头是从「尾」指向「头」的。
-
有向路径：相邻顶点的序列。
-
有向环：一条至少含有一条边且起点和终点相同的有向路径。
❔ 起点和终点相同不是至少两条边吗（A →B, B→A），为什么这里写的是「至少含有一条边」
有一种情况叫做自环（loop），对 \(E\) 中的边 \(e = (u,v)\)，若 \(u = v\)，则 \(e\) 被称作一个自环。
图 1-3 自环示意图 -
有向无环图（DAG）：没有环的有向图。
-
度（degree）：与该顶点相关联的边的条数，顶点 \(v\) 的度记作 \(d(v)\)。
- 入度（in-degree）：与其关联的各边之中，以其为终点的边数，记作 \(d^-(v)\)。
- 出度（out-degree）：以该顶点为起点的边数，记作 \(d^+(v)\)。
📚 更多关于度
若 \(d(v) = 0\) ，则称 \(v\) 为孤立点 (isolated vertex)。
若 \(d(v) = 1\)，则称 \(v\) 为叶节点 (leaf vertex)/悬挂点 (pendant vertex)。
若 \(2 \mid d(v)\)，则称 \(v\) 为偶点 (even vertex)。
若 \(2 \nmid d(v)\)，则称 \(v\) 为奇点 (odd vertex)。图中奇点的个数必然有偶数个（握手定理 推论）。
若 \(d(v) = \left| V \right| - 1\)，则称 \(v\) 为 支配点 (universal vertex)。
- 强连通图和强连通分量：在有向图中，如果所有结点两两互相可达，则称该图为强连通的 (strongly connected)。否则，将其中的极大连通子图称为强连通分量。
- 弱连通图和弱连通分量：若一张有向图的边替换为无向边后可以得到一张连通图，则原来这张有向图是弱连通的 (weakly connected)，将其中的极大弱连通子图称为弱连通分量 。
- 反图 (transpose graph) ：一个有向图 \(G = (V, E)\) 的反图指的是点集不变，每条边反向得到的图。
- 完全图 (complete digraph)：若有向图 \(G\) 满足任意不同两点间均有两条方向不同的边，则称 \(G\) 为有向完全图 。
（2）无向图
Ⅰ. 定义
边没有方向的图称为无向图。
Ⅱ. 术语
- 无向边：无向图中的边被称为无向边（undirected edge)），简称边（edge）。设 \(e = (u,v)\)，则 \(u\) 和 \(v\) 称为 \(e\) 的端点 (endpoint)。
- 相邻：若一个顶点是一条边的端点，则称这个点与这条边是关联的（incident）或相邻的 （adjacent）。两个顶点之间如果有边连接，则称这两个顶点是相邻的（adjacent）。一个顶点 \(v \in V\) 的邻域 (neighborhood) 是所有与之相邻的顶点所构成的集合，记作 \(N(v)\)。
- 路径：相邻顶点的序列。
- 圈：起点和终点重合的路径。
- 连通图：在无向图中，如果从顶点 \(vi\) 到顶点 \(vj\) 有路径，则称 \(vi\) 和 \(vj\) 连通。如果图中任意两个顶点之间都连通，则称该图为连通图，否则，将其中的极大连通子图称为连通块/连通分量。
- 度：顶点连接的边数叫做这个顶点的度。
- 树：没有圈的连通图。
- 森林：没有圈的非连通图。
- 完全图 (complete graph)：若无向简单图 \(G\) 满足任意不同两点间均有边，则称 \(G\) 为完全图，\(n\) 阶完全图记作 \(K_n\) 。
习题讲解 「#19884. 无根树转有根树」
原题目链接 link
「我的做题历程」：
step1：观察题面。
「输入一个 \(n\) 个节点的无根树的各条边，并指定一个根节点，要求把该树转化为有根树，输出各个节点的父亲编号。」，大概能感受到的，是 DFS 遍历无根树。
「根节点的父结点输出-1」，还有要注意的，根节点的本没有父亲，在这里我们需要输出 \(-1\)。
step2：思考解法。
我的想法是先双向存边，然后 DFS 遍历整棵树，在遍历时设置两个参数：当前节点编号，父亲结点编号（上一个节点的编号）。遍历与当前节点相关联的点，除自己的父亲以外，其余都是他的儿子。
step3：完成代码。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e2 + 5;
int n, u, v, fa[N];
vector<int> a[N];
void dfs(int node, int dad) {
fa[node] = dad; // 记录父亲
for (int i = 0; i < a[node].size(); i++) {
if (a[node][i] != dad) {
dfs(a[node][i], node); // 当前节点为相关节点的父亲节点
}
}
return;
}
int main() {
scanf("%d", &n);
for (int i = 1; i < n; i++) {
scanf("%d %d", &u, &v);
a[u].push_back(v); // 双向存边
a[v].push_back(u);
}
int root;
scanf("%d", &root);
dfs(root, -1); // 根没有父亲
for (int i = 0; i < n; i++) {
printf("%d\n", fa[i]);
}
return 0;
}
（二）图的表示（存储结构）
「如何用计算机来存储图的信息（顶点、边），这是图的存储结构要解决的问题？」——cqbzgm's PPT
1. 直接存边
（1）基本思想
使用结构体来存边，结构体内包含一条边的起点和终点（带权图中还能存边权）。也可以用数组分别存上述信息。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
struct Edge {
int x, y, w;
} e[M];
void add(int x, int y, int w) {
e[++tot].x = x, e[tot].y = y, e[tot].w = w;
return;
}
（2）复杂度
- 查询是否存在某条边：\(O(m)\)。
- 遍历一个点的所有出边：\(O(m)\)。
- 遍历整张图：\(O(nm)\)。
- 空间复杂度：\(O(m)\)。
（3）应用
可以用于反转边的方向，Kruskal 算法也需要这样存边。
2. 邻接矩阵
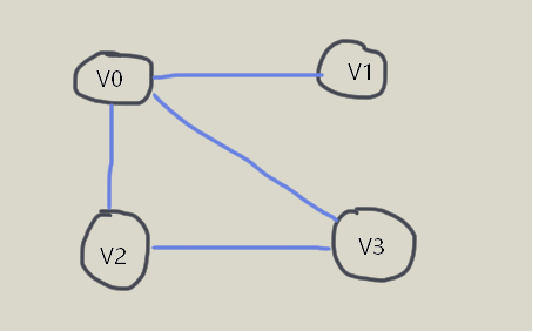
（1）基本思想
对于一个有 \(V\) 个的顶点的图而言，可以使用 \(V\times V\) 的二维数组表示。
\(G_{i, j}\) 表示的是顶点 \(i\) 与顶点 \(j\) 的关系。\(G_{i, j} = 1\) 表示存在 \(i\) 到 \(j\) 的边；如果顶点 \(i\) 和顶点 \(j\) 之间无边相连，\(G_{i, j} = 0\)。如果是带边权的图，可以在 \(G_{i, j}\) 中存储 \(i\) 到 \(j\) 的边的边权。
注：对于无向图：\(G_{i, j} = G_{j, i}\)。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 5;
int n, m, u, v;
bool G[N][N];
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &u, &v);
G[u][v] = G[v][u] = true;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (G[i][j]) {
printf("%d ", j);
}
}
putchar('\n');
}
return 0;
}
各种邻接矩阵
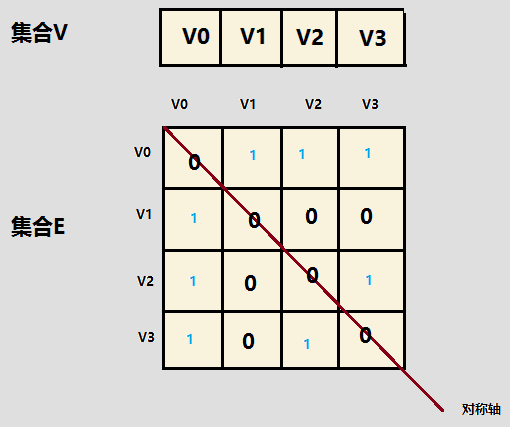
（1）无向图的邻接矩阵
在无向图中，任一顶点 \(i\) 的度为第 \(i\) 列（或第 \(i\) 行）所有非零元素的个数。特别地，无向图的邻接矩阵沿主对角线对称。
（2）有向图的邻接矩阵
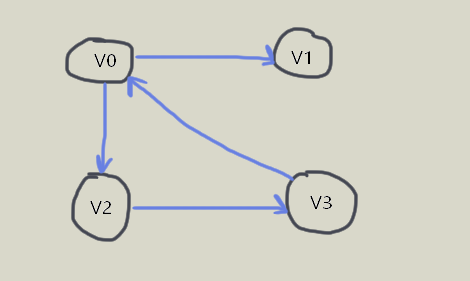
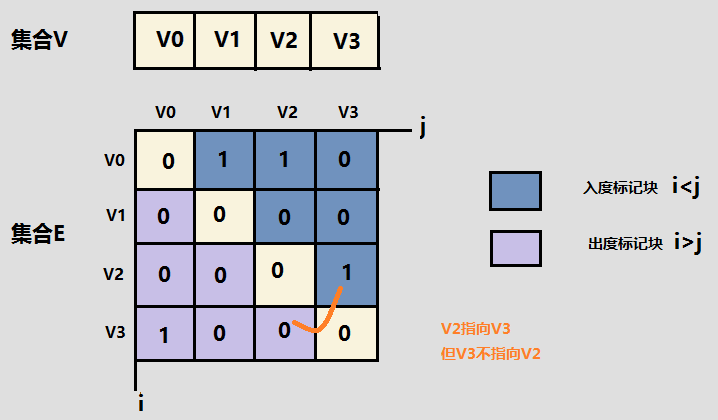
在有向图中，顶点 \(i\) 的出度为：第 \(i\) 行所有非零元素的个数；入度为：第 \(i\) 列所有非零元素的个数。
（3）带权图的邻接矩阵
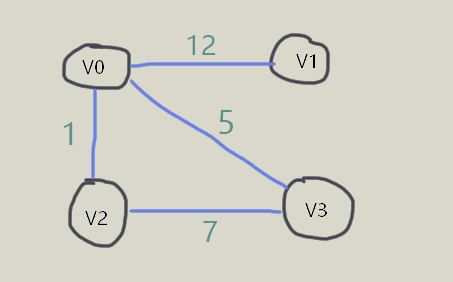
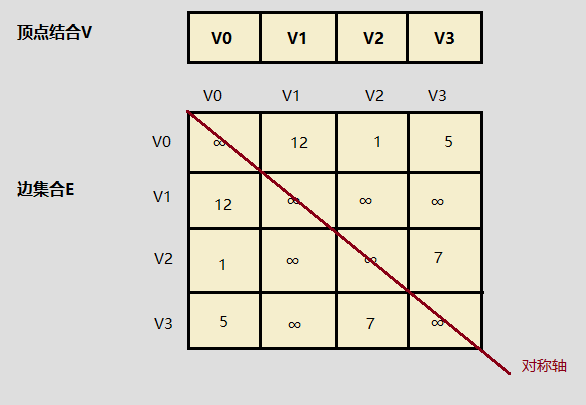
在有向图中，顶点 \(i\) 的出度为：第 \(i\) 行所有非零元素的个数；入度为：第 \(i\) 列所有非零元素的个数。在带权图中，如果在边不存在的情况下，将 \(G[i][j]\) 设置为 \(0\)，则无法与权值为 \(0\) 的情况分开，因此选择较大的常数 \(\text{INF}\) 即可。
（2）复杂度
- 查询是否存在某条边：\(O(1)\)。
- 遍历一个点的所有出边：\(O(n)\)。
- 遍历整张图：\(O(n^2)\)。
- 空间复杂度：\(O(n^2)\)。
（3）应用
使用 Floyd 时会用到，存稠密图很划算。
其优点在于可以在常数时间内判断两点之间是否有边存在；但其缺点是表示稀疏图时，会浪费大量内存空间。
习题演练集
#3373. 「基础算法」求一个有向图中指定顶点的出度
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e2 + 5;
int n, m, u, v, d[N];
vector<int> a[N];
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &u, &v);
a[u].push_back(v);
}
int root;
scanf("%d", &root);
printf("%d", a[root].end() - a[root].begin());
return 0;
}
#25447. 邻接矩阵存储图
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 5;
int n, m, u, v;
bool a[N][N];
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &u, &v);
a[u][v] = a[v][u] = true;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (a[i][j]) {
printf("%d ", j);
}
}
putchar('\n');
}
return 0;
}
3. 邻接表
（1）基本思想
使用一个动态数组（譬如 vector<int> a[N]） 来存边，存储该点的所有出边的相关信息。
链式前向星
链式前向星其实就是静态建立的邻接表，时间效率为 \(O(m)\)，空间效率也为 \(O(m)\)。遍历效率也为 \(O(m)\)。
struct Edge {
int to, w, next;
} edge[M];
void add(int x, int y, int z) {
edge[++tot].to = y, edge[tot].w = z, // 这条边的信息
edge[tot].next = head[x], // 当前边的前驱
head[x] = tot; // 起点 u 的最后一条边
return;
}
for (int i = head[u]; i; i = e[i].next) { // 遍历 u 的出边
int v = e[i].to;
}
各种邻接表
（1）无向图的邻接表
在无向图中，任一顶点 \(i\) 的度为第 \(i\) 列（或第 \(i\) 行）所有非零元素的个数。特别地，无向图的邻接矩阵沿主对角线对称。
（2）有向图的邻接表(出边表、入边表)
出边表的表结点存放的是从表头结点出发的有向边所指的尾顶点，入边表（逆邻接表）的表结点存放的则是指向表头结点的某个头顶点。
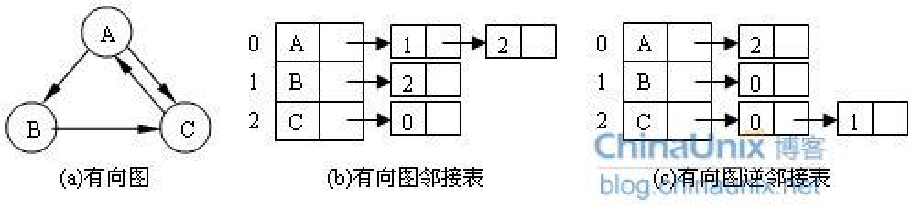
（3）带权图的邻接表
在表结点中增加一个存放权的字段。
（2）复杂度
- 查询是否存在某一条边：\(O(d^+(u))\)。
- 遍历点 \(u\) 的所有出边：\(O(d^+(u))\)。
- 遍历整张图：\(O(n + m)\)。
- 空间复杂度：\(O(m)\)。
（3）应用
存图很适合，内存占用少，但不能快速查询一条边是否存在，也不能直接对一个点的出边进行排序。
特点在于边是带编号的，在遍历边时很方便。如果 tot 的初始值为奇数，存双向边时 \(i \oplus 1\) 即是 \(i\) 的反边（详见《算法竞赛》p63）。
习题演练集
#25448. 邻接表存储图
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
const int N = 1e3 + 5;
int n, m, u[N], v[N];
struct node {
int id, d;
} a[N];
vector<node> G[N];
bool cmp(node x, node y) { return x.d == y.d ? x.id < y.id : x.d < y.d; }
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) {
a[i].id = i;
a[i].d = 0;
}
for (int i = 1; i <= m; i++) {
scanf("%d %d", &u[i], &v[i]);
a[u[i]].d++;
a[v[i]].d++;
}
for (int i = 1; i <= m; i++) {
G[u[i]].push_back(a[v[i]]);
G[v[i]].push_back(a[u[i]]);
}
for (int i = 1; i <= n; i++) {
sort(G[i].begin(), G[i].end(), cmp);
for (int j = 0; j < G[i].size(); j++) {
printf("%d ", G[i][j].id);
}
putchar('\n');
}
return 0;
}
#25449. 邻接表存储带权的无向图
代码（抵制学术不端行为，拒绝 Ctrl + C）：
// 链式前向星
#include <bits/stdc++.h>
using namespace std;
const int N = 2e2 + 5, M = 1e3 + 5;
int n, m, u[N], v[N], w[N], head[M], tot;
struct line {
int u, v, w;
} a[N];
struct Edge {
int to, w, next;
} edge[M];
void add(int x, int y, int z) {
edge[++tot].to = y, edge[tot].w = z,
edge[tot].next = head[x], head[x] = tot;
return;
}
bool cmp(line x, line y) {
if (x.w == y.w) {
return x.v > y.v;
} else {
return x.w > y.w;
}
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d %d", &a[i].u, &a[i].v, &a[i].w);
}
sort(a + 1, a + m + 1, cmp);
for (int i = 1; i <= m; i++) {
add(a[i].u, a[i].v, a[i].w);
add(a[i].v, a[i].u, a[i].w);
}
for (int i = 1; i <= n; i++) {
for (int j = head[i]; j; j = edge[j].next) {
printf("%d ", edge[j].to);
}
putchar('\n');
}
return 0;
}
（三）图的遍历
从图中的某个顶点出发，按某种方法对图中的所有顶点访问且仅访问一次。为了保证图中的顶点在遍历过程中仅访问一次，要为每一个顶点设置一个访问标志。
(没什么好讲的，就照搬课件吧)
(他们都在搞笑，我也要！！1heihei)
1. DFS
(不撞南墙不回头——cqbzgm)
深度优先搜索 (Depth-First Search) 遍历类似于树的先根遍历，是树的先根遍历的推广。
假设初始状态是图中所有顶点未曾被访问，则深度优先搜索可从图中某个顶点 \(v\) 出发，访问此顶点，然后依次从 \(v\) 的未被访问的邻接点出发深度优先遍历图，直至图中所有和 \(v\) 有路径相通的顶点都被访问到；若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。
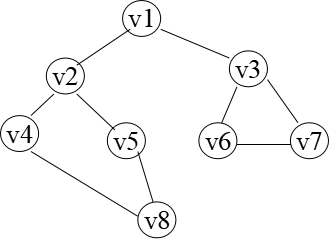
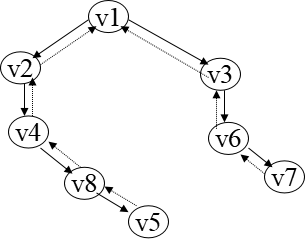
2. BFS
(一石激起千层浪——cqbzgm)
广度优先搜索 (Breadth-First Search) 遍历类似于树的按层次遍历的过程。
假设从图中某顶点 \(v\) 出发，在访问 \(v\) 之后依次访问 \(v\) 的各个邻接点中未被访问过的，然后分别从这些邻接点出发依次访问它们的邻接点，并使「先被访问的顶点的邻接点」先于「后被访问的顶点的邻接点」被访问，直至图中所有已被访问的顶点的邻接点都被访问到。若此时图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。
换句话说，广度优先搜索遍历图的过程是以 \(v\) 为起始点，由近至远，依次访问和 \(v\) 有路径相通且路径长度为 \(1,\ 2,\ …\) 的顶点。
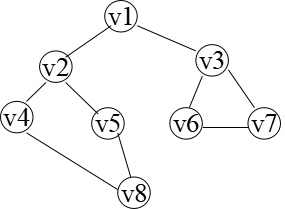
习题演练集
#3376. 有向图的DFS
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e2 + 5;
int n, m, u, v, d[N];
bool vis[N];
vector<int> a[N];
void dfs(int node, int fa) {
vis[node] = true;
printf("%d ", node);
sort(a[node].begin(), a[node].end());
for (int i = 0; i < a[node].size(); i++) {
if (a[node][i] != fa && !vis[a[node][i]]) {
dfs(a[node][i], node);
}
}
return;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &u, &v);
a[u].push_back(v);
}
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
dfs(i, -1);
}
}
return 0;
}
#3377. 有向图的BFS
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e2 + 5;
int n, m, u, v, d[N];
bool vis[N];
vector<int> a[N];
void bfs(int node) {
vis[node] = true;
queue<int> q;
q.push(node);
int x;
while (q.size()) {
x = q.front();
q.pop();
printf("%d ", x);
sort(a[x].begin(), a[x].end());
for (int i = 0; i < a[x].size(); i++) {
if (!vis[a[x][i]]) {
q.push(a[x][i]);
vis[a[x][i]] = true;
}
}
}
return;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &u, &v);
a[u].push_back(v);
}
for (int i = 1; i <= n; i++) {
if (!vis[i]) {
bfs(i);
}
}
return 0;
}
#3424. 有向图的连通度
该题等价于是求图的传递闭包。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 2e3 + 5;
int n, m, u, v, t, sum[N];
bitset<N> G[N]; // 可以用 bitset 优化
char ch;
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("\n");
for (int j = 1; j <= n; j++) {
ch = getchar();
G[i][j] = ch - '0';
}
G[i][i] = true;
}
ll cnt = 0;
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (G[i][j])
G[i] |= G[j]; // 如果他们联通就合并他们能到达的点
}
}
for (int i = 1; i <= n; i++) { // 防止有的集合在不完整时就与其它集合合并
for (int j = 1; j <= n; j++) {
if (G[i][j])
G[i] |= G[j];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
cnt += G[i][j];
}
}
printf("%lld", cnt);
return 0;
}
#3380. 「Uva 10004」二染色
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
const int N = 2e2 + 5;
int n, m, u, v, c[N];
bool check;
bitset<N> vis;
vector<int> G[N];
void dfs(int node, int fa, int color) {
if (!check) {
return;
}
c[node] = color;
for (int i = 0; i < G[node].size(); i++) {
if (!c[G[node][i]]) {
dfs(G[node][i], node, -color);
} else {
if (-color != c[G[node][i]]) {
check = false;
return;
}
}
}
return;
}
int main() {
while (~scanf("%d", &n) && n) {
scanf("%d", &m);
for (int i = 0; i < n; i++) {
G[i].clear();
c[i] = 0;
vis[i] = false;
}
for (int i = 1; i <= m; i++) {
scanf("%d %d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
check = true;
c[0] = 1;
dfs(0, -1, 1);
if (check) {
printf("BICOLORABLE\n");
} else {
printf("NOT BICOLORABLE\n");
}
}
return 0;
}
#3304. 一笔画问题
一笔画问题的代码实现关键在于：当每次遍历过一条边时，就把这条边删掉，这样就不会重复遍历。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e3 + 5;
int n, m, u, v, d[N];
bool a[N][N];
void dfs(int node) {
for (int i = n; i >= 1; i--) {
if (a[node][i]) {
a[node][i] = a[i][node] = false;
dfs(i);
}
}
printf("%d ", node);
return;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &u, &v);
a[u][v] = true, d[u]++;
a[v][u] = true, d[v]++;
}
int id = 1;
for (int i = 1; i <= n; i++) {
if (d[i] & 1) {
id = i;
break;
}
}
dfs(id);
return 0;
}
#3378. 哈密顿路问题
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <cstdio>
#include <vector>
#include <bitset>
using namespace std;
const int N = 2e2 + 5;
int n, op, cnt;
bitset<N> vis;
vector<int> a[N];
void dfs(int node, int sum) {
if (sum == n) {
cnt++;
return;
}
vis[node] = true;
for (int i = 0; i < a[node].size(); i++) {
if (!vis[a[node][i]]) {
vis[a[node][i]] = true;
dfs(a[node][i], sum + 1);
vis[a[node][i]] = false;
}
}
return;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
scanf("%d", &op);
if (op) {
a[i].push_back(j);
}
}
}
for (int i = 1; i <= n; i++) {
vis.reset();
dfs(i, 1);
}
printf("%d", cnt);
return 0;
}
二、最短路
性质
- 对于边权为正的图，任意两个结点之间的最短路，不会经过重复的结点；
- 对于边权为正的图，任意两个结点之间的最短路，不会经过重复的边；
- 对于边权为正的图，任意两个结点之间的最短路，任意一条路上的结点数不会超过总结点数（以后简称 \(n\)），边数不会超过 \(n - 1\)。
（一）Floyd 算法
Floyd 算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与 Dijkstra 算法类似。
该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。
1. 基本原理
- 从任意一条单边路径开始。任意两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大（常设 \(\text{INF}=\text{0x3f3f3f3f}\)）；
- 对于每一对顶点 \(u\) 和 \(v\)，查询是否存在一个顶点 \(w\) 使得从 \(u\) 到 \(w\) 再到 \(v\) 比已知的路径更短。如果就是更新它。
Tips: 一般 \(N\) 的很小的最短路才用 Floyd。
2. 算法描述
初始化：
把图用邻接矩阵 \(f\) 表示出来，如果从 \(v_i\) 到 \(v_j\) 有路可达，则 \(f_{i, j} = d\)，\(d\) 表示该路的长度；否则 \(f_{i, j} = +\infty\)。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
f[i][j] = INF; // 初始化为极大值（在这里可以看做无穷大）
}
f[i][i] = 0; // 自己到自己的距离是 0
}
for (int i = 1; i <= m; i++) {
scanf("%d %d %d", &u, &v, &w);
f[u][v] = f[v][u] = min(f[u][v], w); // 处理重边（具体取长取短视题目而定）
}
算法部分：
\(\text{Part1}\) 计算最短路
运用动态规划的思想。我们定义一个三维数组 \(f_{k, i, j}\)，表示只允许经过前 \(k\) 个结点，结点 \(i\) 到结点 \(j\) 的最短路长度。
明显地，\(f_{n, i, j}\) 就是结点 \(i\) 到结点 \(j\) 的最短路长度。
于是我们顺手就可以写出 Floyd 的状态转移方程（\(f_{k - 1, i, j}\) 表示不经过 \(k\) 点，\(f_{k - 1, i, k} + f_{k - 1, k, j}\) 表示经过 \(k\) 点）：
通过上式可以发现，第一维只代表阶段的转移，对结果无影响。于是乎，第一维可以被省略，转而在原有基础上迭代（但要保证 \(k\) 的循环一定是正序）。
状态转移方程又变为：
抹去第一维的操作为我们节省了大把空间，也使 Floyd 的适用范围更广。
\(\text{Part2}\) 输出路径
若要输出路径，则需要定义一个矩阵 \(pre\) 用来记录所经过点的信息，\(pre_{i, j}\) 表示从 \(i\) 到 \(j\) 所经过的结点中，\(i\) 号结点的后一个结点，初始化为 \(pre_{i, j} = i\)。在 \(f\) 中包含有两点之间最短道路的信息，而在 \(pre\) 中则包含了最短路路径的信息。多源最短路计算加上路径输出，这才是完整的 Floyd 算法。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
// 初始化示意
for (int i = 1; i <= m; i++) {
scanf("%d %d %d", &x, &y, &w);
if (f[x][y] > w) {
f[y][x] = f[x][y] = w;
pre[x][y] = y;
pre[y][x] = x;
}
}
// Floyd
void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (f[i][j] >= f[i][k] + f[k][j]) { // 可以更新或本身就在最短路上的结点都要记录
if (f[i][j] == f[i][k] + f[k][j] && i != k) {
pre[i][j] = min(pre[i][j], pre[i][k]); // 一般题目会要求字典序最小且经过边最少，所以要比 min
} else if (f[i][j] > f[i][k] + f[k][j]) { // 更新最短路
f[i][j] = f[i][k] + f[k][j];
pre[i][j] = pre[i][k]; // 这个时候就直接赋值
}
}
}
}
}
return;
}
算法结束：
\(f_{i, j}\)得出的就是任意起点 \(i\) 到任意终点 \(j\) 的最短路径。
3. 讨论
\(\text{Part1}\) 为什么枚举中转点的循环k要放在最外层？
Floyd 的原始状态转移方程为：
由此，可以发现第一维的 \(k\) 其实表示的是不同的阶段，枚举着不同情况下的所有结果，而并不是在枚举中转点，必须放在最外层（譬如区间 DP 中，长度 \(len\) 就是一个阶段，放在最外层，代表合并不同数量的单元时，其不同的最优结果）。若认为 \(k\) 是决策（即枚举 \(i \to j\) 的中间点），将 \(k\) 放在最里层循环中，便会得到错误的结果。
所以，我们可以得到：\(k\) 不是在枚举中转点，而是在表示 DP 的阶段，故阶段循环必须放在最外层。
4. 复杂度
- 时间复杂度：\(O(n^3)\)；
- 空间复杂度：\(O(n^2)\)。
习题讲解 「#47253. 最短路上的统计」
原题目链接 link
「我的做题历程」：
（敢情我爆了一道弱智题）
step1：观察题面。
「一个无向图上，没有自环，所有边的权值均为1，对于一个点对（a,b） 我们要把所有a与b之间所有最短路上的点的总个数输出。」，不是吧，就这。（实际蒟蒻被打脸了）
step2：思考解法。
刚开始想复杂了，莫名其妙做出了一股区间 DP 的味道。
(hh，xswl)
然而，只需要先求出最短路再暴力枚举路径累加即可。
step3：完成代码。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <cstdio>
using namespace std;
const int N = 1e2 + 5, INF = 0x3f3f3f3f;
int n, m, a, b, p, f[N][N], sum[N][N];
void Floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++){
for (int j = 1; j <= n; j++) {
if (f[i][j] > f[i][k] + f[k][j]) {
f[i][j] = f[i][k] + f[k][j];
}
}
}
}
for (int k = 1; k <= n; k++) { // 就，就感觉自己挺弱智的
for (int i = 1; i <= n; i++){
for (int j = 1; j <= n; j++) {
if (f[i][j] == f[i][k] + f[k][j]) {
sum[i][j]++;
}
}
}
}
return;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
f[i][j] = INF;
}
f[i][i] = 0;
}
for (int i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
f[a][b] = f[b][a] = 1;
}
Floyd();
scanf("%d", &p);
for (int i = 1; i <= p; i++) {
scanf("%d %d", &a, &b);
printf("%d\n", sum[a][b]);
}
return 0;
}
习题讲解 「#76. Sightseeing Trip」
原题目链接 link
「我的做题历程」：
step1：观察题面。
「给定一张无向图，求图中一个至少包含 \(3\) 个点的环，环上的节点不重复，并且环上的边的长度之和最小。」，（看到这里我人都傻了，啥？最小环？） 。无向图求最小环的话，应该要先求多源最短路，毕竟在输入时我们无法确定哪个是环上的点。
「在本题中，你需要输出最小环的方案，若最小环不唯一，输出任意一个均可。若无解，输出 No solution.」，特别提醒：无解的 「No solution.」最末有一个句号（看漏的自觉打脸，我已经开始打了）。
step2：思考解法。
刚开始没有想法，直到看见题解。
(kaiwanxiao'o)
既然要求最小环，首先这一定是一个简单环，那这个环一定可以被分成 \(i \to j\) 和 \(j \to i\) 两部分，但如果要求一个环至少包含三个点的话，仅仅需要 \(i\to \cdots j \to k \to i\) 就够了。故问题变成：求 \((f_{i, j} + w_{j, k} + w_{k, i})_{min}\) 。
step3：完成代码。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
const int N = 2e2 + 5;
int n, m;
long long w[N][N], f[N][N], pre[N][N], minn = 1e12, a, b, c;
// 十年 OI 一场空，不开 long long 见祖宗
vector<int> ans;
void get(int x, int y) {
if (!pre[x][y]) {
return ;
}
get(x, pre[x][y]);
ans.push_back(pre[x][y]);
get(pre[x][y], y);
return;
}
void floyd() {
for (int k = 1; k <= n; k++) {
// 求只经过前 k 个点的最小环
for (int i = 1; i < k; i++) {
for (int j = i + 1; j < k; j++) { // 防止与 i 重复
// {k, i, j} 代表经过前 k 个点 从 i 到 j 的最短路径
// 若 i，j 均不取 k，则一定不会经过第 k 个点
if (f[i][j] + w[j][k] + w[k][i] < minn) {
// 环的路线：i -> ... -> j -> k -> i
// 虽然这里只枚举了 i < j 的情况，但由无向图的对称性可知 j > i 的情况与 i < j 的情况是相同的
minn = f[i][j] + w[j][k] + w[k][i];
ans.clear(); // 若被更新则答案清零
ans.push_back(i);
get(i, j); // 填补 i -> j 中间的点
ans.push_back(j);
ans.push_back(k);
}
}
}
// 求只经过前 k 个点的最短路径
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (f[i][k] + f[k][j] < f[i][j]) {
f[i][j] = f[i][k] + f[k][j];
pre[i][j] = k; // 记录 i 的后继（后一个点）
}
}
}
}
return;
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
f[i][j] = w[i][j] = 1e12;
}
f[i][i] = w[i][i] = 0;
}
for (int i = 1; i <= m; i++) {
scanf("%lld %lld %lld", &a, &b, &c);
w[b][a] = w[a][b] = f[b][a] = f[a][b] = min(f[a][b], c);
// 为了方便的求环，需要记录权值
}
floyd();
if (minn == 1e12) {
printf("No solution.");
return 0;
}
for (int i = 0; i < ans.size(); i++) {
printf("%lld ", ans[i]);
}
return 0;
}
习题演练集
#3608. 跑步(Floyd模板)
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
const int N = 2e1 + 5;
int n, k, x, a, b;
double c, f[N][N];
bool vis[N][N];
void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
}
}
}
return;
}
int main() {
scanf("%d %d %d", &n, &k, &x);
memset(f, 127, sizeof f);
for (int i = 1; i <= k; i++) {
scanf("%d %d %lf", &a, &b, &c);
if (vis[a][b]) {
f[a][b] = max(f[a][b], c); // 注意读题
} else {
f[a][b] = c;
vis[a][b] = true;
}
if (vis[b][a]) {
f[b][a] = max(f[b][a], c);
} else {
f[b][a] = c;
vis[b][a] = true;
}
}
for (int i = 1; i <= n; i++) {
f[i][i] = 0;
}
floyd();
for (int i = 1; i <= x; i++) {
scanf("%d %d", &a, &b);
if (f[a][b] - int(f[a][b])) { // 判断小数点后是否有数（判断是否为浮点数）
printf("%.1lf\n", f[a][b]);
} else {
printf("%d\n", int(f[a][b]));
}
}
return 0;
}
#6235. GF和猫咪的玩具
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
const int N = 1e2 + 5;
int n, m, a, b, f[N][N], ans;
void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
}
}
}
return;
}
int main() {
scanf("%d %d", &n, &m);
memset(f, 0x3f, sizeof f);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
f[a][b] = 1; // 无向图跑 Floyd 需跑双向边
f[b][a] = 1;
}
for (int i = 1; i <= n; i++) {
f[i][i] = 0;
}
floyd();
ans = 0;
for (int i = 1; i <= n; i++) {
for (int j = i + 1; j <= n; j++) {
// printf("%d ", f[i][j]);
ans = max(ans, f[i][j]);
}
// putchar('\n');
}
printf("%d", ans);
return 0;
}
#8171. 「基础算法」最短路径问题
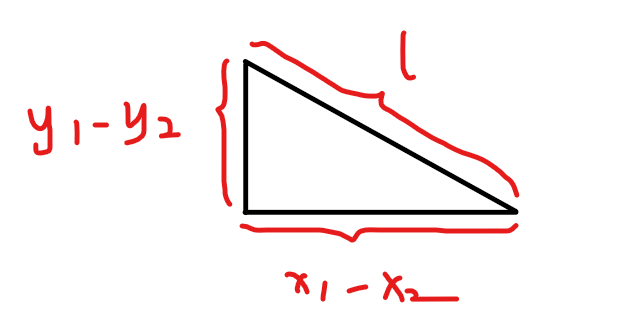
这里需要引入一下勾股定理：两直角边的平方和等于斜边的平方。此处 \((x_1 - x_2)^2 + (y_1 - y_2)^2 = l^2\)。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
const int N = 1e2 + 5;
int n, m, c, d, s, t;
double f[N][N];
bool vis[N][N];
struct node {
double x, y;
} a[N];
void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
}
}
}
return;
}
int main() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
f[i][j] = 0x7f7f7f7f;
}
f[i][i] = 0;
}
for (int i = 1; i <= n; i++) {
scanf("%lf %lf", &a[i].x, &a[i].y);
}
scanf("%d", &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &c, &d);
f[c][d] = min(f[c][d], sqrt((a[c].x - a[d].x) * (a[c].x - a[d].x) + (a[c].y - a[d].y) * (a[c].y - a[d].y))); // 求两点间的直线距离可以使用勾股定理
f[d][c] = f[c][d];
}
floyd();
scanf("%d %d", &s, &t);
printf("%.2lf\n", f[s][t]);
return 0;
}
#3147. 多源最短路
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
const int N = 5e2 + 5, INF = 0x3f3f3f3f;
int n, x, f[N][N], ans;
void init() {
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
f[i][i] = 0;
for (int j = 1; j <= n; j++) {
f[i][j] = INF;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
scanf("%d", &x);
f[i][j] = min(f[i][j], x);
}
}
}
void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
f[i][j] = min(f[i][j], f[i][k] + f[k][j]);
}
}
}
return;
}
void solve() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
printf("%d ", f[i][j]);
}
putchar('\n');
}
return;
}
int main() {
init();
floyd();
solve();
return 0;
}
#30135. 多源最短路方案
原题目链接 link
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 1e2 + 5, M = 2 * 5e3 + 5, INF = 0x3f3f3f3f;
ll n, m, q, x, y, w, f[N][N], pre[N][N];
void init() {
scanf("%lld %lld %lld", &n, &m, &q);
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
f[i][j] = INF;
}
f[i][i] = 0;
}
for (int i = 1; i <= m; i++) {
scanf("%lld %lld %lld", &x, &y, &w);
if (f[x][y] > w) {
f[y][x] = f[x][y] = w;
pre[x][y] = y;
pre[y][x] = x;
}
}
return;
}
void floyd() {
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (f[i][j] >= f[i][k] + f[k][j]) {
if (f[i][j] == f[i][k] + f[k][j] && i != k) {
pre[i][j] = min(pre[i][j], pre[i][k]);
} else if (f[i][j] > f[i][k] + f[k][j]){
f[i][j] = f[i][k] + f[k][j];
pre[i][j] = pre[i][k];
}
}
}
}
}
return;
}
void print(ll node) {
if (!pre[node][y]) {
return;
}
printf("%lld ", node);
print(pre[node][y]);
return;
}
void solve() {
for (int i = 1; i <= q; i++) {
scanf("%lld %lld", &x, &y);
if (f[x][y] == INF) {
printf("-1\n");
} else {
printf("%lld\n", f[x][y]);
print(x);
printf("%lld\n", y);
}
}
return;
}
int main() {
init();
floyd();
solve();
return 0;
}
（二）Dijkstra 算法
Dijkstra 算法是从一个顶点到其余各顶点的最短路径算法，解决的是非负权图中的单源最短路问题。
该算法由荷兰计算机科学家 E. W. Dijkstra 于 1959 年提出。
1. 基本原理
- 结点分成两组：已经确定最短路（记作 \(S\) 集合）、尚未确定最短路（记作 \(T\) 集合）；
- 初始化 \(dis\) 数组为 \(+\infty\)，\(dis_s = 0\) ；
- 不断从 \(T\) 中选择路径长度最短的点放入 \(S\)。
- 对那些刚刚加入 \(S\) 的结点的所有出边执行松弛操作。
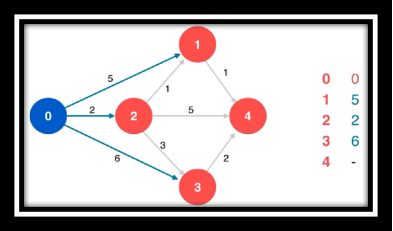
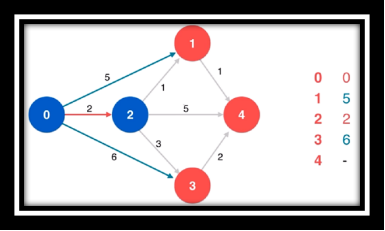
算法过程欣赏（从左往右从上至下）
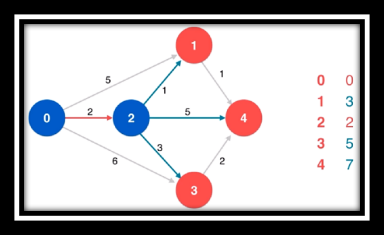
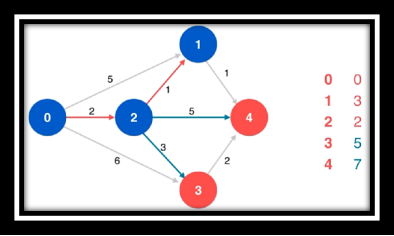
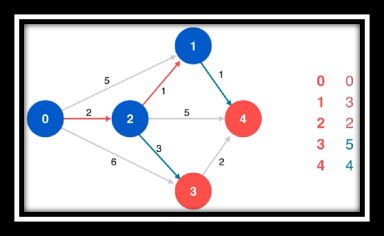
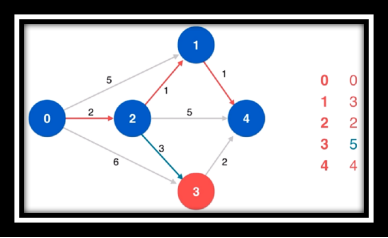
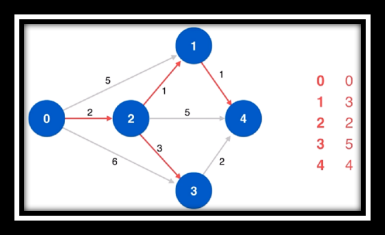
❔ 什么是松弛
举一个形象的
用烂了的🌰（栗子）：
用一根橡皮筋直接连接 \(a,\ b\) 两点，现存一点 \(k\)，使得 \(a \to k \to b\) 比 \(a \to b\) 的距离更短。把橡皮筋改为 \(a \to k \to b\) 后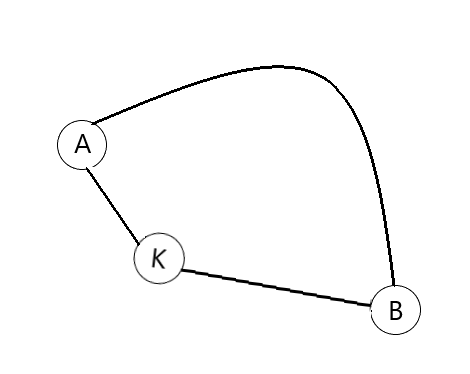 ，橡皮筋更加松弛。
图 2-1 松弛示意图
更严谨的定义：松弛操作是指对于每个顶点 \(v\in V\)，都设置一个属性 \(dis_v\)，用来描述从源点 \(s\) 到 \(v\) 的最短路径上权值的上界，称为最短路径估计（shortest-path estimate）。
2. 算法描述
初始化：
设起点为 \(s\)，\(dis[v]\) 表示从指定起点 \(s\) 到 \(v\) 的最短路径，\(pre_v\) 为 \(v\) 的前驱，用来输出路径。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
for (int i = 1; i <= n; i++) {
dis[i] = INF; // 初始化为极大值（在这里可以看做无穷大）
vis[i] = false; // 最开始所有点都没有确定最短路
pre[i] = 0;
}
dis[s] = 0;
vis[s] = true;
算法部分：
\(\text{Part1}\) 计算最短路
朴素算法 \(O(n^2)\)：
- 在没有被访问过的点中找一个相邻顶点 \(k\)，使得 \(dis_k\) 是最小的；
- \(k\) 标记为已确定的最短路 \(vis_k=\text{true}\);
- 用 for 循环更新与 \(k\) 相连的每个未确定最短路径的顶点 \(v\) (所有未确定最短路的点都松弛更新)。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
for (int i = 1; i <= n; i++) {
dis[i] = INF, vis[i] = false;
}
dis[s] = 0; //初始化源点到源点最短路权 0
vis[i] = true; //初始化源点已经是最短路点
for (int i = 1; i < n; i++) { //枚举没被设定为最短路的点
int minn = INF, k; //找源点到j点的最短路的点
for (int j = 1; j <= n; j++) {
if (!vis[j] && dis[j] < minn) {
minn = dis[j];
k = j;
}
}
vis[k] = true; //将k点标记为已找到最短路
for (int j = 1; j <= n; j++) { //松弛未标记最短路的点
if (dis[j] > dis[k] + w[k][j]) {
dis[j] = dis[k] + w[k][j];
}
}
}
printf("%d", dis[t]);
优先队列优化：
我们可以发现，如果边数远小于 \(n^2\)，对此可以考虑用优先队列进行优化，取出最短路径的复杂度降为 \(O(\log m)\)；可以用链式前向星存边来优化每次松弛的复杂度，其复杂度降为 \(O(e)\)（\(e\) 为该点的边数）。
如果同一个点的最短路被更新多次，而先前更新时插入的元素不能被删除，也不能被修改，只能留在优先队列中，故优先队列内的元素个数是 \(m\)，时间复杂度为 \(O(m\log m)\)。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
void Dijkstra() {
memset(dis, 0x7f, sizeof dis);
memset(vis, 0, sizeof vis);
dis[s] = 0;
q.push(make_pair(0, s));
int x;
while (q.size()) {
x = q.top().second;
q.pop();
if (vis[x]) {
continue;
}
vis[x] = true;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to, w = e[i].w;
if (dis[y] > dis[x] + w) {
dis[y] = dis[x] + w;
q.push(make_pair(-dis[y], y));
}
}
}
return;
}
\(\text{Part2}\) 输出路径
若要输出路径，则需要定义一个一维数组 \(pre\) 用来记录所经过点的信息，\(pre_{i}\) 表示 \(i\) 号结点的前一个结点。
代码（抵制学术不端行为，拒绝 Ctrl + C）：
struct Edge { // 链式前向星存储
int to, w, next;
} e[M];
void add(int u, int v, int w) {
e[++tot].to = v, e[tot].w = w,
e[tot].next = head[u], head[u] = tot;
return;
}
int dis[N];
bool vis[N];
priority_queue< pair<int, int> > q;
void Dijkstra() {
for (int i = 1; i <= n; i++) {
dis[i] = INF;
vis[i] = false;
}
dis[s] = 0;
q.push(make_pair(0, s));
int x;
while (q.size()) {
x = q.top().second;
q.pop();
if (vis[x]) {
continue;
}
vis[x] = true;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to, w = e[i].w;
if (dis[y] > dis[x] + w) {
dis[y] = dis[x] + w;
pre[y] = x;
q.push(make_pair(-dis[y], y));
} else if (dis[y] == dis[x] + w) {
pre[y] = min(pre[y], x);
}
}
}
return;
}
void print(int node) {
if (!node) {
return;
}
print(pre[node]);
printf("%d ", node);
return;
}
void solve() {
if (dis[t] == INF) {
printf("no solution");
} else {
printf("%d\n", dis[t]);
print(t);
}
return;
}
算法结束：
\(dis_v\)为 \(s\) 到 \(v\) 的最短路距离；\(pre_v\) 为 \(v\) 的前驱结点，用来输出路径。
3. 讨论
\(\text{Part1}\) 为什么 Dijkstra 不能用于负权图？
在 Dijkstra 的正确性证明中，关键不等式 \(D(y) \le D(u)\) 是在图上所有边边权非负的情况下得出的。当图上存在负权边时，这一不等式不再成立，Dijkstra 算法的正确性将无法得到保证，算法可能会给出错误的结果。
Dijkstra 算法的正确性证明（摘自 OI Wiki）
下面用数学归纳法证明，在所有边权值非负的前提下，Dijkstra 算法的正确性。
简单来说，我们要证明的，就是在执行 1 操作时，取出的结点 最短路均已经被确定，即满足 \(D(u) = dis(u)\)。
初始时 \(S \ne \varnothing\)，假设成立。
接下来用反证法。
设 \(u\) 点为算法中第一个在加入 \(S\) 集合时不满足 \(D(u) = dis(u)\) 的点。因为 \(s\) 点一定满足 ，且它一定是第一个加入 \(S\) 集合的点，因此将 \(u\) 加入 \(S\) 集合前，\(S \ne \varnothing\)，如果不存在 \(s\) 到 \(u\) 的路径，则 \(D(u) = dis(u) = +\infty\)，与假设矛盾。
于是一定存在路径 \(s \to x \to y \to u\)，其中 \(y\) 为 \(s \to u\) 路径上第一个属于 \(T\) 集合的点，而 \(x\) 为 \(y\) 的前驱结点（显然 \(x \in S\)）。需要注意的是，可能存在 \(s = x\) 或 \(y = u\) 的情况，即 \(s \to x\) 或 \(y \to u\) 可能是空路径。
因为在 \(u\) 结点之前加入的结点都满足 \(D(u) = dis(u)\)，所以在 \(x\) 点加入到 \(S\) 集合时，有 \(D(x) = dis(x)\)，此时边 \((x,\ y)\) 会被松弛，从而可以证明，将 \(u\) 加入到 \(S\) 时，一定有 \(D(y) = dis(y)\)。
下面证明 \(D(u) = dis(u)\) 成立。在路径 \(s \to x \to y \to u\) 中，因为图上所有边边权非负，因此 \(D(y) \le dis(y)\)。从而 \(dis(y) \le D(y) \le D(u) \le dis(u)\)。但是因为 \(u\) 结点在 1 过程中被取出 \(T\) 集合时， 结点还没有被取出 \(T\) 集合，因此此时有 \(dis(u) \le dis(y)\)，从而得到 \(dis(y) = D(y) = D(u) = dis(u)\)，这与 \(D(u) \ne dis(u)\) 的假设矛盾，故假设不成立。
因此我们证明了，1 操作每次取出的点，其最短路均已经被确定。命题得证。
4. 复杂度
- 时间复杂度：\(O(n^2)\)（普通的）；\(O(n\log n)\sim O(m\log n)\)（堆优化的）；
- 空间复杂度：\(O(n)\)。
习题演练集
#8172. 单源点最短路问题
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <cstdio>
#include <queue>
using namespace std;
typedef long long ll;
const int N = 2e3 + 5, M = 2 * 1e4 + 5, INF = 0x3f3f3f3f;
int n, m, a, b, c, s, t, tot, head[N], pre[N];
struct Edge {
int to, w, next;
} e[M];
void add(int u, int v, int w) {
e[++tot].to = v, e[tot].w = w,
e[tot].next = head[u], head[u] = tot;
return;
}
void init() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d %d", &a, &b, &c);
add(a, b, c);
}
scanf("%d %d", &s, &t);
return;
}
int dis[N];
bool vis[N];
priority_queue< pair<int, int> > q;
void Dijkstra() {
for (int i = 1; i <= n; i++) {
dis[i] = INF;
vis[i] = false;
}
dis[s] = 0;
q.push(make_pair(0, s));
int x;
while (q.size()) {
x = q.top().second;
q.pop();
if (vis[x]) {
continue;
}
vis[x] = true;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to, w = e[i].w;
if (dis[y] > dis[x] + w) {
dis[y] = dis[x] + w;
pre[y] = x;
q.push(make_pair(-dis[y], y));
} else if (dis[y] == dis[x] + w) {
pre[y] = min(pre[y], x);
}
}
}
return;
}
void print(int node) {
if (!node) {
return;
}
print(pre[node]);
printf("%d ", node);
return;
}
void solve() {
printf("%d\n", dis[t]);
print(t);
return;
}
int main() {
init();
Dijkstra();
solve();
return 0;
}
#8169. 有向图的单源点最短路径
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <cstdio>
#include <queue>
using namespace std;
typedef long long ll;
const int N = 2e3 + 5, M = 2 * 1e4 + 5, INF = 0x3f3f3f3f;
int n, m, a, b, c, s, t, tot, head[N], pre[N];
struct Edge {
int to, w, next;
} e[M];
void add(int u, int v, int w) {
e[++tot].to = v, e[tot].w = w,
e[tot].next = head[u], head[u] = tot;
return;
}
void init() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &a, &b);
add(a, b, 1);
}
scanf("%d %d", &s, &t);
return;
}
int dis[N];
bool vis[N];
priority_queue< pair<int, int> > q;
void Dijkstra() {
for (int i = 1; i <= n; i++) {
dis[i] = INF;
vis[i] = false;
}
dis[s] = 0;
q.push(make_pair(0, s));
int x;
while (q.size()) {
x = q.top().second;
q.pop();
if (vis[x]) {
continue;
}
vis[x] = true;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to, w = e[i].w;
if (dis[y] > dis[x] + w) {
dis[y] = dis[x] + w;
pre[y] = x;
q.push(make_pair(-dis[y], y));
} else if (dis[y] == dis[x] + w) {
pre[y] = min(pre[y], x);
}
}
}
return;
}
void print(int node) {
if (!node) {
return;
}
print(pre[node]);
printf("%d ", node);
return;
}
void solve() {
if (dis[t] == INF) {
printf("no solution");
} else {
printf("%d\n", dis[t]);
print(t);
}
return;
}
int main() {
init();
Dijkstra();
solve();
return 0;
}
#3144. 无向图单源最短路
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <bits/stdc++.h>
using namespace std;
const int N = 2505, M = 12205;
int n, m, s, t, c, d, z, dis[N], head[N], tot;
bool vis[M];
struct Edge {
int to, w, next;
} e[M];
priority_queue<pair<int, int> > q;
void add(int u, int v, int w) {
e[++tot].to = v, e[tot].w = w,
e[tot].next = head[u], head[u] = tot;
return;
}
void dijkstra() {
memset(dis, 0x7f, sizeof dis);
memset(vis, 0, sizeof vis);
dis[s] = 0;
q.push(make_pair(0, s));
int x;
while (q.size()) {
x = q.top().second;
q.pop();
if (vis[x]) {
continue;
}
vis[x] = true;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to, w = e[i].w;
if (dis[y] > dis[x] + w) {
dis[y] = dis[x] + w;
q.push(make_pair(-dis[y], y));
}
}
}
return;
}
int main() {
scanf("%d %d %d %d", &n, &m, &s, &t);
for (int i = 1; i <= m; i++) {
scanf("%d %d %d", &c, &d, &z);
add(c, d, z);
add(d, c, z);
}
dijkstra();
printf("%d", dis[t]);
return 0;
}
（三）Bellman-Ford 算法
Bellman-Ford 算法是求解单源最短路径问题的一种算法。
该算法由理查德·贝尔曼（Richard Bellman）和莱斯特·福特创立。有时候这种算法也被称为 Moore-Bellman-Ford 算法，因为 Edward F. Moore 也为这个算法的发展做出了贡献。
其优于 Dijkstra 算法的方面是边的权值可以为负数、实现简单，缺点是时间复杂度过高，高达 \(O(VE)\)。但算法可以进行若干种优化，提高效率。
1. 基本原理
对图进行 \(V-1\) 次松弛操作，得到所有可能的最短路径。
算法过程欣赏（从左往右从上至下）
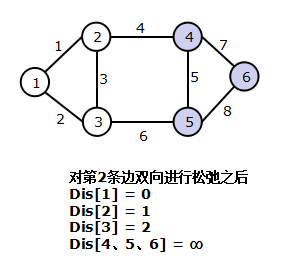
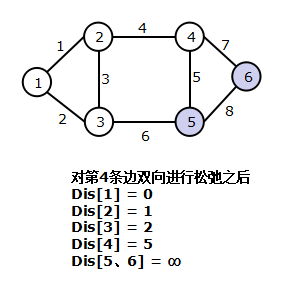
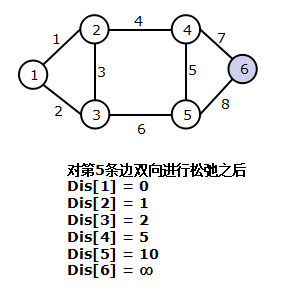
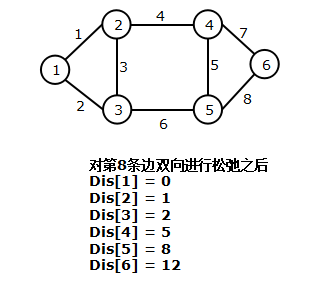
2. 算法描述
代码（抵制学术不端行为，拒绝 Ctrl + C）：
int dis[N];
void Bellman_Ford() {
for (int i = 1; i <= n; i++) {
dis[i] = INF;
}
dis[s] = 0;
for (int i = 1; i < n; i++) { // 松弛 n - 1 次
for (int j = 1; j <= m; j++) { // 对每一条边进行松弛
int y = e[j].y, x = e[j].x;
if (dis[y] > dis[x] + e[j].w) {
dis[y] = dis[x] + e[j].w;
}
}
}
return;
}
3. 讨论
\(\text{Part1}\) 在 Bellman-Ford 算法中怎样判有向环？
当从 \(s\) 点出发，抵达一个负环时，松弛操作会无休止地进行下去。在 Bellman-Ford 中，对于最短路存在的图，松弛操作最多只会执行 \(n - 1\) 轮。因此，如果第 \(n\) 轮循环时仍然存在能松弛的边，说明从 \(s\) 点出发，能够抵达一个负环。
需要注意的是，以 \(s\) 点为源点跑 Bellman-Ford 算法时，如果没有给出存在负环的结果，只能说明从 \(s\) 点出发不能抵达一个负环，而不能说明图上不存在负环。（譬如 #91. 「Vijos P1053」Easy SSSP，就是血与泪的教训）
因此如果需要判断整个图上是否存在负环，最严谨的做法是建立一个超级源点（正常一点说，虚点），向图上每个节点连一条权值为 \(0\) 的边，然后以超级源点为起点执行 Bellman-Ford 算法。
\(\text{Part2}\) Bellman-Ford 可以优化吗？
是的，很多时候我们并不需要那么多无用的松弛操作。
很显然，只有上一次被松弛的结点，所连接的边，才有可能引起下一次的松弛操作。
那么我们用队列来维护「哪些结点可能会引起松弛操作」，就能只访问必要的边了。
这种做法就是我们接下来要记载的 SPFA 算法。（除此之外还有堆优化、栈优化、LLL 优化、SLF 优化，D´Esopo-Pape 算法等奇形怪状杂七杂八优美的优化可以自行了解）
4. 复杂度
- 时间复杂度：\(O(nm)\)；
- 空间复杂度：\(O(n)\)。
习题演练集
#2848. 非负权单源最短路
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <algorithm>
#include <cstdio>
#include <queue>
using namespace std;
const int M = 12400 + 5, N = 2.5e3+ 5, INF = 0x3f3f3f3f;
int n, m, a, b, c, s, t, tot;
struct Edge {
int u, v, w;
} e[M];
void add(int u, int v, int w) {
e[++tot].u = u, e[tot].v = v,e[tot].w = w;
return;
}
void init() {
scanf("%d %d %d %d", &n, &m, &s, &t);
for (int i = 1; i <= m; i++) {
scanf("%d %d %d", &a, &b, &c);
add(a, b, c);
add(b, a, c);
}
return;
}
int dis[N];
void Bellman_Ford() {
for (int i = 1; i <= n; i++) {
dis[i] = INF;
}
dis[s] = 0;
for (int i = 1; i < n; i++) {
for (int j = 1; j <= 2 * m; j++) {
int x = e[j].u, y = e[j].v, w = e[j].w;
if (dis[y] > dis[x] + w) {
dis[y] = dis[x] + w;
}
}
}
return;
}
void solve() {
printf("%d", dis[t]);
}
int main() {
init();
Bellman_Ford();
solve();
return 0;
}
#9890. 带负权单源点最短路
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <algorithm>
#include <cstdio>
using namespace std;
const int M = 4e4 + 5, N = 5e2 + 5, INF = 0x3f3f3f3f;
int n, m, a, b, c, s, t, tot, pre[M];
struct Edge {
int x, y, w;
} e[M];
void add(int u, int v, int w) {
e[++tot].x = u, e[tot].y = v, e[tot].w = w;
return;
}
void init() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d %d", &a, &b, &c);
add(a, b, c);
}
scanf("%d %d", &s, &t);
return;
}
void print(int node) {
if (!pre[node]) {
return;
}
print(pre[node]);
printf("%d ", node);
return;
}
int dis[N];
void Bellman_Ford() {
for (int i = 1; i <= n; i++) {
dis[i] = INF;
}
dis[s] = 0;
for (int i = 1; i < n; i++) {
for (int j = 1; j <= m; j++) {
int y = e[j].y, x = e[j].x;
if (dis[y] > dis[x] + e[j].w) {
dis[y] = dis[x] + e[j].w;
pre[y] = x;
}
if (dis[y] == dis[x] + e[j].w) {
pre[y] = min(pre[y], x);
}
}
}
for (int i = 1; i <= m; i++) {
int y = e[i].y, x = e[i].x;
if (dis[y] > dis[x] + e[i].w) {
printf("No Solution");
return;
}
}
printf("%d\n%d ", dis[t], s);
print(t);
return;
}
int main() {
init();
Bellman_Ford();
return 0;
}
（四）SPFA 算法
SPFA 算法是 Bellman-Ford算法的队列优化算法的别称，通常用于求含负权边的单源最短路径，以及判负权环。SPFA 最坏情况下复杂度和朴素 Bellman-Ford 相同，为 \(O(VE)\)。
SPFA算法的全称是：Shortest Path Faster Algorithm，是西南交通大学段凡丁于 1994 年发表的论文中的名字。不过，段凡丁的证明是错误的，且在 Bellman-Ford 算法提出后不久（1957 年）已有队列优化内容，所以国际上不承认 SPFA 算法是段凡丁提出的。
1. 基本原理
先将源点加入队列。然后从队列中取出一个点（此时该点为源点），对该点的邻接点进行松弛，如果该邻接点松弛成功且不在队列中，则把该点加入队列。如此循环往复，直到队列为空，则求出了最短路径。
2. 算法描述
代码（抵制学术不端行为，拒绝 Ctrl + C）：
void print(int node) {
if (!pre[node]) {
return;
}
print(pre[node]);
printf("%d ", node);
return;
}
int dis[N];
bool vis[N];
queue<int> q;
void SPFA() {
for (int i = 1; i <= n; i++) {
dis[i] = INF, vis[i] = false;
}
dis[s] = 0, vis[s] = true, q.push(s);
int x;
while (q.size()) {
x = q.front();
q.pop();
vis[x] = false;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to, w = e[i].w;
if (dis[y] > dis[x] + e[i].w) {
dis[y] = dis[x] + e[i].w;
pre[y] = x;
if (!vis[y]) {
q.push(y);
vis[y] = true;
}
}
else if (dis[y] == dis[x] + e[i].w) {
pre[y] = min(pre[y], x);
}
}
}
if (dis[t] == INF) {
printf("-1");
} else {
printf("%d\n%d ", dis[t], s);
print(t);
}
return;
}
3. 讨论
\(\text{Part1}\) 在 SPFA 算法中怎样判有向环？
如果某个点进入队列的次数超过 \(n\) 次则存在负环 ( 存在负环则无最短路径，如果有负环则会无限松弛,而一个带 \(n\) 个点的图至多松弛 \(n-1\) 次) 。
\(\text{Part2}\) 怎样看待「SPFA」已死的说法？
（emm...怎么说呢）段凡丁于 1994 年发表的论文中给出了 SPFA 算法的证明。不过，段凡丁的证明是错误的，段凡丁论文中时间复杂度的证明 （\(O(KE)\)，\(K\) 是常数）也是错误的。该算法的最坏复杂度为 \(O(VE)\)。
段凡丁的论文（部分）
段凡丁论文里的 SPFA 正确性证明分成两部分：一定能找到最短路；算法能在有限次操作后找到最短路。从他的代码和证明来看，他当时并没有想到负环的情况（即每个点至多入队 \(n-1\) 次），他这个代码一旦有负环就停不下来了。
他的复杂度证明的也是很奇妙，仅凭实验就断定算法的复杂度，而没有理论上的证明，显然是行不通的。所以 SPFA 这个算法不是很受待见，在某乎上就有「SPFA 这玩意，既然都知道它复杂度是扯淡的，那它就应该被当成一个骗分算法。」，「如果出题人不卡骗分算法，就是不尊重写 dij 的选手。卡 SPFA 是出题人负责任的体现」，甚至还有专门卡 SPFA 的数据。
说句老实话，在无恶意数据下跑负权图的 SPFA 确实挺快。而且有一部分题比较适合用 SPFA。SPFA 被卡了也就是个 Bellman-Ford 的时间复杂度，不用白不用嘛，当然正权图里还是 Dijkstra 好。
4. 复杂度
- 时间复杂度：\(O(nm)\)；
- 空间复杂度：\(O(n)\)。
习题演练集
#30143. 非负权单源最短路（强化版）
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <algorithm>
#include <cstdio>
#include <queue>
using namespace std;
const int M = 2e6 + 5, N = 1e6 + 5, INF = 0x3f3f3f3f;
int n, m, a, b, c, s, t, tot, head[N];
struct Edge {
int to, w, next;
} e[M];
void add(int u, int v, int w) {
e[++tot].to = v, e[tot].w = w,
e[tot].next = head[u], head[u] = tot;
return;
}
void init() {
scanf("%d %d %d %d", &n, &m, &s, &t);
for (int i = 1; i <= m; i++) {
scanf("%d %d %d", &a, &b, &c);
add(a, b, c);
add(b, a, c);
}
return;
}
int dis[N];
bool vis[N];
queue<int> q;
void SPFA() {
for (int i = 1; i <= n; i++) {
dis[i] = INF;
}
dis[s] = 0;
vis[s] = true;
q.push(s);
int x;
while (q.size()) {
x = q.front();
q.pop();
vis[x] = false;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to, w = e[i].w;
if (dis[y] > dis[x] + w) {
dis[y] = dis[x] + w;
if (!vis[y]) {
q.push(y);
vis[y] = true;
}
}
}
}
return;
}
void solve() {
if (dis[t] == INF) {
printf("-1");
} else {
printf("%d", dis[t]);
}
return;
}
int main() {
init();
SPFA();
solve();
return 0;
}
#30144. 非负权单源最短路（输出方案）
代码（抵制学术不端行为，拒绝 Ctrl + C）：
#include <algorithm>
#include <cstdio>
#include <queue>
using namespace std;
const int M = 2e6 + 5, N = 1e6 + 5, INF = 0x3f3f3f3f;
int n, m, a, b, c, s, t, tot, head[N], pre[N];
struct Edge {
int to, w, next;
} e[M];
void add(int u, int v, int w) {
e[++tot].to = v, e[tot].w = w,
e[tot].next = head[u], head[u] = tot;
return;
}
void init() {
scanf("%d %d %d %d", &n, &m, &s, &t);
for (int i = 1; i <= m; i++) {
scanf("%d %d %d", &a, &b, &c);
add(a, b, c);
add(b, a, c);
}
return;
}
int dis[N];
bool vis[N];
queue<int> q;
void SPFA() {
for (int i = 1; i <= n; i++) {
dis[i] = INF;
}
dis[s] = 0;
vis[s] = true;
q.push(s);
int x;
while (q.size()) {
x = q.front();
q.pop();
vis[x] = false;
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to, w = e[i].w;
if (dis[y] > dis[x] + w) {
dis[y] = dis[x] + w;
pre[y] = x;
if (!vis[y]) {
q.push(y);
vis[y] = true;
}
} else if (dis[y] == dis[x] + w) {
pre[y] = min(pre[y], x);
}
}
}
return;
}
void print(int node) {
if (!pre[node]) {
return;
}
print(pre[node]);
printf(" %d", node);
return;
}
void solve() {
if (dis[t] == INF) {
printf("-1");
} else {
printf("%d\n%d", dis[t], s);
print(t);
}
return;
}
int main() {
init();
SPFA();
solve();
return 0;
}
三、最小生成树
百度百科定义：一个有 \(n\) 个结点的连通图的生成树是原图的极小连通子图，且包含原图中的所有 \(n\) 个结点，并且有保持图连通的最少的边。
OI Wiki：我们定义无向连通图的最小生成树（Minimum Spanning Tree，MST）为边权和最小的生成树。
注意：只有连通图才有生成树，而对于非连通图，只存在生成森林。
（一）Prim 算法
普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。
该算法于 \(1930\) 年由捷克数学家沃伊捷赫·亚尔尼克（英语：Vojtěch Jarník）发现；并在 \(1957\) 年由美国计算机科学家罗伯特·普里姆（英语：Robert C. Prim）独立发现。因此，在某些场合，普里姆算法又被称为 DJP 算法、亚尔尼克算法或普里姆－亚尔尼克算法。
1. 基本原理
- 以任意一个点为基准点；
- 节点分为两组：
- 在 MST 上到基准点的路径已经确定的点；
- 尚未在 MST 中与基准点相连的点。
- 不断从第2组中选择与第1组距离最近的点加入第1组。
注：类似于 Dijkstra，本质也是贪心，\(O(n^2)\)
对图进行 \(V-1\) 次松弛操作，得到所有可能的最短路径。
1. 基本原理
先将源点加入队列。然后从队列中取出一个点（此时该点为源点），对该点的邻接点进行松弛，如果该邻接点松弛成功且不在队列中，则把该点加入队列。如此循环往复，直到队列为空，则求出了最短路径。
算法过程欣赏（动图）
2. 算法描述
代码（抵制学术不端行为，拒绝 Ctrl + C）：
ll d[N];
bool vis[N];
priority_queue< pair<ll, int > > q;
void Prim() {
for (int i = 1; i <= n; i++) {
d[i] = INF;
}
d[1] = 0;
q.push(make_pair(0, 1));
int x;
while (q.size()) {
x = q.top().second;
q.pop();
if (vis[x]) {
continue;
}
vis[x] = true;
MST += d[x];
for (int i = head[x]; i; i = e[i].next) {
int y = e[i].to;
ll w = e[i].w;
if (d[y] > w) {
d[y] = w;
q.push(make_pair(-d[y], y));
}
}
}
return;
}
3. 讨论
\(\text{Part1}\) Prim 和 Kruskal 的区别？
Prim 算法的本质是不断加点（而不是 Kruskal 算法的加边）。
4. 复杂度
- 时间复杂度：\(O(n^2+ m)\)（普通的）；\(O((n + m)\log n)\sim O(m\log n)\)（堆优化的）
（二）Kruskal 算法
Kruskal 算法是一种常见并且好写的最小生成树算法，由 Kruskal 发明。该算法的基本思想是从小到大加入边，是个贪心算法。
Kruskal 算法适合于求边稀疏的网的最小生成树。
1. 基本原理
-
以任意一个点为基准点；
-
节点分为两组：
- 在 MST 上到基准点的路径已经确定的点；
- 尚未在 MST 中与基准点相连的点。
-
不断从第2组中选择与第1组距离最近的点加入第1组。
注：类似于 Dijkstra，本质也是贪心，\(O(n^2)\)
对图进行 \(V-1\) 次松弛操作，得到所有可能的最短路径。
1. 基本原理
- 利用并查集，起初每个点各自构成一个集合；
- 所有边按照边权从小到大排序，依次扫描；
- 若当前扫描到的边连接两个不同的点集就合并。
注：本质也是贪心，\(O(m\log n)\)。与 Prim 算法相比，没有基准点，该算法是不断选择两个距离最近的集合进行合并的过程。
算法过程欣赏（动图）
2. 算法描述
代码（抵制学术不端行为，拒绝 Ctrl + C）：
void MakeSet() {
for (int i = 1; i <= n; i++) {
fa[i] = i;
}
return;
}
int FindSet(int node) {
if (fa[node] == node) {
return node;
}
return fa[node] = FindSet(fa[node]);
}
void UnionSet(int x, int y) {
x = FindSet(x), y = FindSet(y);
if (x == y) {
return;
}
fa[x] = y;
return;
}
bool cmp(Edge x, Edge y) { return x.w < y.w; }
void Kruskal() {
MakeSet();
sort(e + 1, e + n, cmp);
int x, y, w;
for (int i = 1; i < n; i++) {
x = FindSet(e[i].u), y = FindSet(e[i].v), w = e[i].w;
UnionSet(x, y);
}
return;
}
3. 复杂度
- 时间复杂度：\(O(m \log m)\)
未完待续。。。
叭叭~(≧∇≦)ﾉ
