「题解」锦鲤序列

（锦鲤：为何如此之晦……）

原题目链接：link

「我的做题历程」：

step1：观察题面。

  「锦鲤序列的长度一定是奇数，前 \(n+1\) 个数一定是严格单调递增的，后 \(n+1\) 个数一定是严格单调递减的，找到这个整数序列中最长的锦鲤序列」 ，明显的，该题是最长上升子序列的应用。（题型：线性 dp —— 最长上升子序列）

step2：思考解法。

第一步，思考 dp 状态：

\(dp1_{i}\)：从左至右找到分界点 \(i\) （可以不包括 \(i\) 点）的最长上升子序列长度。

\(dp2_{i}\)：从左至右找到分界点 \(i\) （可以不包括 \(i\) 点）的最长上升子序列长度。

第二步，思考答案位置：

  由于锦鲤序列两端对称，且长度为奇数，所以对于每一个 \(i\) ，\(ans = \max\{ans, 2 \times \min \{dp1_i,dp2_i\} - 1\}\)。

Q1：如果是 \(O(n\log n)\) 的算法，\(i\) 点不一定被算过两次，那为什么一定要 \(-1\)？

A：

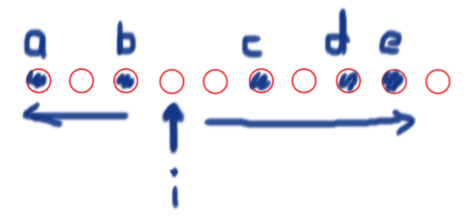
  请看下方示意图。记当前分界点为 \(i\)，两边的最长上升子序列为 \(f1, f2\) ，\(f1 = \{a, b\}\ (a\lt b)\)，\(f2 = \{c, d, e\}\ (e\lt d\lt c)\) 。

  若两个子序列都包含 \(i\) ，那 \(-1\) 是无疑的。当出现如下情况时，由于锦鲤序列两端对称，所以会舍弃掉 \(f2\) 数组的一个元素。不妨假设舍弃元素 \(e\) ，剩下的数长度为偶数，不符题意，所以要再舍弃一个。

  不妨假设在 \(b, c\) 中舍弃一个。若 \(b=c\) ，舍弃哪个都无所谓；若 \(b > c\) ，则一定能舍去 \(c\)（若 \(b > c\) ，则 \(b > d\)）；同理，若 \(b < c\) ，则一定能舍去 \(b\)。

  所以无论 \(i\) 点是否被算过，最后都要 \(-1\)。

Q2：上图，如果 \(c\) 大于 \(b\)，则答案应该是 \(5\)，可算出来 \(3\) 不就错了吗？

A：

  若 \(c\) 大于 \(b\) ，则长度确实该是 \(5\) ，但这样看就忽略了一点，\(i\) 会枚举 \(1\sim n\) 的每一个元素，当 \(i\) 枚举到 \(c\) 时，数组划分成 \(f1 = \{a,b,c \},\ f2 = \{c,d,e\}\)，答案会更新到 5。因此对于一段代码绝不能就局部而纠结，要从宏观来观察它的作用。

step3：完成代码。

代码（抵制学术不端行为，拒绝 Ctrl + C）：

#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5; 
int n, a[N], dp[N], dp2[N], s[N], ans;
int main() {
	freopen("koi.in", "r", stdin);
	freopen("koi.out", "w", stdout);
	scanf("%d", &n);
	for (int i = 1; i <= n; i++) {
		scanf("%d", a + i);
	}
	int len = 0;
	dp[0] = dp[n + 1] = -1e9;
	for (int i = 1; i <= n; i++) {
		if (dp[len] < a[i]) {
			dp[++len] = a[i];
		}
		dp[lower_bound(dp + 1, dp + len + 1, a[i]) - dp] = a[i];
		s[i] = len;
	}
	len = 0;
	for (int i = n; i >= 1; i--) {
		if (dp2[len] < a[i]) {
			dp2[++len] = a[i];
		}
		dp2[lower_bound(dp2 + 1, dp2 + len + 1, a[i]) - dp2] = a[i];
		s[i] = min(s[i], len);
	}
	for (int i = 1; i <= n; i++) {
		ans = max(ans, 2 * s[i] - 1);
	}
	printf("%d", ans);
	return 0;
} 

锦鲤保佑我拿到 Accepted

---

让我们来解决 『锦鲤序列』 叭~

Bye bye!!1 👋👋