2022.5.14 全盘题解
序言
生活不易,锦鲤无语。
其实个人感觉 『还好』,不至于完全没思路。
(投放 My blogs😃。)
来吧,上题!(对题有疑问可以直接问)
A. 零钱兑换
Give me your money!!1
「我的做题历程」:
step1:观察题面,这可以让我们了解题的类型。
「编写一个函数来计算可以凑成总金额」,可以得出这是一道背包 DP。
「每种硬币的数量是无限的」,进一步得出这是道完全背包。(题型:完全背包)
「最少的硬币个数」,证明这要在背包的前提下,求出最小组成数量。
「多组测试数据」,谨记多组输入 (论 Wrong Answer 与没有多组输入)。(注意:多组输入)
step2:思考解法。
第一步,思考 dp 状态:
\(dp_{i,j}\):前 \(i\) 种硬币凑出面值 \(j\) 的最少币数。
对于当前一种硬币 \(coins_{i}\) 而言,只有取或不取两种状态。
若取,取后的币数为前 \(i - 1\) 种硬币凑出面值 \(j-w_{i}\times k\) 的总币数加上当前种类所需币数 \(k\)。
若不取,则说明前 \(i - 1\) 种硬币已经能够凑出面值 \(j\),不需要再取。
第二步,思考状态转移方程:
原本完全背包的状态转移方程是:
但这里我们并不是求总金额以内最大能凑出的面值,而是求凑成总金额的最少币数,于是就有:
通过观察发现,上述方程可以降维。由于对 \(dp_{i}\) 有影响的只有 \(i - 1\),故可以把前一维抹掉,但需要保证 \(dp_{i,j}\) 可以被 \(dp_{i, j - a_{i}}\) 影响(即 \(dp_{i,j}\) 被计算时 \(dp_{i, j - a_{i}}\) 已经被算出),这才相当于物品 \(i\) 多次被放入背包,所以枚举当前面值 \(j\) 时要正序。
第三步,打出完全背包的代码,把状态转移方程换一下,于是本题的算法部分就完成啦:
for (int i = 1; i <= n; i++) {
for (int j = a[i]; j <= amount; j++) {
dp[j] = min(dp[j], dp[j - a[i]] + 1);
}
}
step3:完成代码:
通过数据范围可以发现,一种硬币的面额是可以比总金额大的,因此可以预处理浅浅优化一下(虽然没什么大的效果)。
因为找的是最小币数,所以 dp 数组要初始化成极大值,而前 \(0\) 种硬币凑成 面值 \(0\) 只需要 \(0\) 种硬币,由此可得 \(dp_{0} = 0\)。
输出时值得注意的是,「如果没有任何一种硬币组合能组成总金额,输出 \(-1\)」;在代码中,这意味着「如果 \(dp_{amount}\) 没有被更新,则输出 \(-1\)」,所以只需要输出时特判一下 \(dp_{amount}\) 若仍是初始值就输出 \(-1\)。
代码(抵制学术不端行为,拒绝 Ctrl + C):
#include <bits/stdc++.h>
using namespace std;
const int N = 1e2 + 5, A = 1e4 + 5, INF = 0x3f3f3f3f;
int n, amount, a[N], dp[A];
/*
dp(i, j): 前 i 个硬币凑出 j 的最少硬币个数
dp(i, j) = min(dp(i - 1, j - a[i]), dp(i - 1, j));
取这个硬币 or 不取这个硬币
*/
int main() {
freopen("exchange.in", "r", stdin);
freopen("exchange.out", "w", stdout);
while (~scanf("%d %d", &n, &amount)) {
memset(dp, 0x3f, sizeof dp);
for (int i = 1; i <= n; i++) {
scanf("%d", a + i);
}
dp[0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = a[i]; j <= amount; j++) {
dp[j] = min(dp[j - a[i]] + 1, dp[j]);
}
}
printf("%d\n", dp[amount] == INF ? -1 : dp[amount]); // 可以使用三目运算符来特判
}
return 0;
}
Accepted 交换给我吧!!1
B. 蝙蝠侠的麻烦
没 事 找 事
「我的做题历程」:
step1:观察题面。
「蝙蝠侠需要找到一个最长的字符串,使得这个字符串作为一个子序列被包含在所有的三个字符串中」,可以得出这是一道最长公共子序列,而且有三个字符串。(题型:线性 dp —— 最长公共子序列)
「蝙蝠侠现在需要找到的是最大的长度,而不是序列」,说明只是一道普通的 LCS。
step2:思考解法。
第一步思考 dp 状态:
\(dp_{i,j,k}\):第一串前 \(i\) 项,第二串前 \(j\) 项,第三串前 \(k\) 项中的最长公共子序列长度。
对于当前的 \(a_{i}, b_{j}, c_{k}\) 而言,只有能做贡献或无法做贡献两种状态。
若 \(a_{i}= b_{j}= c_{k}\),则它们能做贡献,此时的最长公共子序列的长度为第一串前 \(i - 1\) 项,第二串前 \(j - 1\) 项,第三串前 \(k - 1\) 项中的最长公共子序列的长度加 \(1\)。
否则它们无法做贡献,此时放弃做贡献最小的那一项。
第二步思考状态转移方程:
本题比常规的 LCS 要多一个字符串,因此只需要再多一维就好。
step3:完成代码:
因为有三个字符串,所以需要比平常的 LCS 多一层循环。
代码(抵制学术不端行为,拒绝 Ctrl + C):
#include <bits/stdc++.h>
using namespace std;
const int N = 5e1 + 5;
char a[N], b[N], c[N];
int la, lb, lc, dp[N][N][N];
/*
dp(i, j, k): 前 i, j, k 项中的最长公共子序列
if a(i) = b(j) = c(k)
dp(i, j, k) = dp(i - 1, j - 1, k - 1) + 1;
else
dp(i, j, k) = max{dp(i - 1, j, k), dp(i, j - 1, k), dp(i, j, k - 1)};
*/
int main() {
freopen("trouble.in", "r", stdin);
freopen("trouble.out", "w", stdout);
scanf("%s\n%s\n%s", a + 1, b + 1, c + 1);
la = strlen(a + 1), lb = strlen(b + 1), lc = strlen(c + 1);
for (int i = 1; i <= la; i++) {
for (int j = 1; j <= lb; j++) {
for (int k = 1; k <= lc; k++) {
if (a[i] == b[j] && b[j] == c[k]) {
dp[i][j][k] = dp[i - 1][j - 1][k - 1] + 1;
} else {
dp[i][j][k] = max(dp[i - 1][j][k], max(dp[i][j - 1][k], dp[i][j][k - 1]));
}
}
}
}
printf("%d", dp[la][lb][lc]);
return 0;
}
Trouble is a friend, but Accepted is better than it!
C. 带分数
数学老师:你这是最简分数吗你!
这道是深搜,平均用时 \(3000\mathrm{ms}\);个人做法是暴力枚举,用时 \(139\mathrm{ms}\)。
但是我不知道这个同学 (变态) \(130\mathrm{ms}\) 是怎么做到的……

「简述正解(鸣谢 GM 老师)」:
先把 \(1\sim 9\) 的全排列存在 \(a\) 数组中,再将 \(a\) 数组中的 \(9\) 个数分为 \(3\) 段,\(m_1 = \operatorname{sum}(1,i)\)(\(1\sim i\) 区间表示的数) 表示整数(当 \(m_1\le num\) 时不必再算下去)。
\(i + 1\sim 9\) 要分为两段,枚举中间点 \(k\),\(m_2 = \operatorname{sum}(i + 1, k), m_3 = \operatorname{sum}(k + 1, 9)\)。
if (m2 > m3 && m2 % m3 == 0 && num == m1 + m2 / m3) { // 判断是否为解
printf("%d=%d+%d/%d\n", n, m1, m2, m3);
ans++;
}
「我的做题历程」:
step1:观察题面。
「带分数中,数字 \(1\sim 9\) 分别出现且只出现一次(不包含 \(0\)),输出该数字 \(N\) 用数码 \(1\sim 9\) 不重复不遗漏地组成带分数表示的全部种数」,先闪出的是深搜,但由于想不出怎么搜,转战暴力。(题型:DFS or 暴力枚举)\
step2:思考解法。
抓住带分数构成特点:整数+假分数,即 \(x = a + {b\over c}\ (a,b, c \ne 0)\)(假分数可化简为整数,即分子可以整除分母 \((b = kc,\ c\mid b)\) )。
于是想到先枚举前面的整数 \(a\),然后得到后面的假分数化简的结果 \(k\),通过枚举 \(c\) 来得到 \(b\)。再判断 \(a,b,c\) 是否满足题意即可。
总不能无限枚举吧,来估范围。分子最小为 \(1\),则整数部分最小为 \(2\),分母最大可取 \(9876543\),还能得到当数 \(N\) 大于 \(9876545\) 时无解(然而 \(N \le 10^6\) ,这个 \(N\) 的范围毫无用处)。
step3:完成代码。
代码(抵制学术不端行为,拒绝 Ctrl + C):
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
int n, sum;
bool vis[11]; // 用于判断数码是否重复、遗漏
inline bool nosame(int x) { // 判断一个数的数码是否重复
memset(vis, 0, sizeof vis);
while (x != 0) {
if (vis[x % 10] || x % 10 == 0) {
return false;
}
vis[x % 10] = true;
x /= 10;
}
return true;
}
inline int len(int x) { // 获取该数位数(长度)
int l = 0;
while (x != 0) {
l++;
x /= 10;
}
return l;
}
inline bool nopublic(int a, int b, int c) { // 判断带分数中有无重复的数码
memset(vis, 0, sizeof vis);
while (a != 0) {
vis[a % 10] = true;
if (a % 10 == 0) {
return false;
}
a /= 10;
}
while (b != 0) {
if (vis[b % 10] || b % 10 == 0) {
return false;
}
vis[b % 10] = true;
b /= 10;
}
while (c != 0) {
if (vis[c % 10] || c % 10 == 0) {
return false;
}
vis[c % 10] = true;
c /= 10;
}
return true;
}
inline void get(int x) {
int l = len(n - x);
// 枚举倍数
for (int i = 1; i <= 9876543; i++) { // 分子至少为一,整数部分就只能为二,分母最大可取 9876543
if (nosame(x * i) && nosame(i) && nopublic(x * i, i, n - x) && len(x * i) + len(i) + l == 9) {
printf("%d=%d+%d/%d\n", n, n - x, x * i, i);
sum++;
}
if (len(x * i) + len(i) + l > 9) { // 如果数码大于 9 位就不用再算了
break;
}
}
return;
}
int main() {
freopen("fraction.in", "r", stdin);
freopen("fraction.out", "w", stdout);
while (~scanf("%d", &n)) {
sum = 0;
for (int i = 1; i < n; i++) {
if (nosame(i)) {
get(n - i);
}
}
printf("%d\n", sum);
}
return 0;
}
数据 Hack 了呢~你的 Accepted 被 Hack 掉了吗~( ̄y▽, ̄)╭
D. 锦鲤序列
锦鲤:为何如此之晦
「我的做题历程」:
step1:观察题面。
「锦鲤序列的长度一定是奇数,前 \(n+1\) 个数一定是严格单调递增的,后 \(n+1\) 个数一定是严格单调递减的,找到这个整数序列中最长的锦鲤序列」 ,明显的,该题是最长上升子序列的应用。(题型:线性 dp —— 最长上升子序列)
step2:思考解法。
第一步,思考 dp 状态:
\(dp1_{i}\):从左至右找到分界点 \(i\) (可以不包括 \(i\) 点)的最长上升子序列长度。
\(dp2_{i}\):从左至右找到分界点 \(i\) (可以不包括 \(i\) 点)的最长上升子序列长度。
第二步,思考答案位置:
由于锦鲤序列两端对称,且长度为奇数,所以对于每一个 \(i\) ,\(ans = \max\{ans, 2 \times \min \{dp1_i,dp2_i\} - 1\}\)。
Q1:如果是 \(O(n\log n)\) 的算法,\(i\) 点不一定被算过两次,那为什么一定要 \(-1\)?
A:
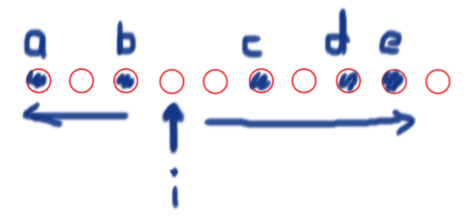
请看下方示意图。记当前分界点为 \(i\),两边的最长上升子序列为 \(f1, f2\) ,\(f1 = \{a, b\}\ (a\lt b)\),\(f2 = \{c, d, e\}\ (e\lt d\lt c)\) 。
若两个子序列都包含 \(i\) ,那 \(-1\) 是无疑的。当出现如下情况时,由于锦鲤序列两端对称,所以会舍弃掉 \(f2\) 数组的一个元素。不妨假设舍弃元素 \(e\) ,剩下的数长度为偶数,不符题意,所以要再舍弃一个。
不妨假设在 \(b, c\) 中舍弃一个。若 \(b=c\) ,舍弃哪个都无所谓;若 \(b > c\) ,则一定能舍去 \(c\)(若 \(b > c\) ,则 \(b > d\));同理,若 \(b < c\) ,则一定能舍去 \(b\)。
所以无论 \(i\) 点是否被算过,最后都要 \(-1\)。
Q2:上图,如果 \(c\) 大于 \(b\),则答案应该是 \(5\),可算出来 \(3\) 不就错了吗?
A:
若 \(c\) 大于 \(b\) ,则长度确实该是 \(5\) ,但这样看就忽略了一点,\(i\) 会枚举 \(1\sim n\) 的每一个元素,当 \(i\) 枚举到 \(c\) 时,数组划分成 \(f1 = \{a,b,c \},\ f2 = \{c,d,e\}\),答案会更新到 5。因此对于一段代码绝不能就局部而纠结,要从宏观来观察它的作用。
step3:完成代码。
代码(抵制学术不端行为,拒绝 Ctrl + C):
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n, a[N], dp1[N], dp2[N], f1[N], f2[N], ans;
int main() {
freopen("koi.in", "r", stdin);
freopen("koi.out", "w", stdout);
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", a + i);
}
int len = 0;
dp1[0] = dp2[n + 1] = -1e9;
for (int i = 1; i <= n; i++) {
if (dp1[len] < a[i]) {
dp1[++len] = a[i];
}
dp1[lower_bound(dp1 + 1, dp1 + len + 1, a[i]) - dp1] = a[i];
f1[i] = len;
}
len = 0;
for (int i = n; i >= 1; i--) {
if (dp2[len] < a[i]) {
dp2[++len] = a[i];
}
dp2[lower_bound(dp2 + 1, dp2 + len + 1, a[i]) - dp2] = a[i];
f2[i] = len;
}
for (int i = 1; i <= n; i++) {
ans = max(ans, 2 * min(f1[i], f2[i]) - 1);
}
printf("%d", ans);
return 0;
}
还可以优化一下,快个 \(20\text{ms}\) 左右。
代码(抵制学术不端行为,拒绝 Ctrl + C):
#include <bits/stdc++.h>
using namespace std;
const int N = 1e5 + 5;
int n, a[N], dp[N], dp2[N], s[N], ans;
int main() {
freopen("koi.in", "r", stdin);
freopen("koi.out", "w", stdout);
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", a + i);
}
int len = 0;
dp[0] = dp[n + 1] = -1e9;
for (int i = 1; i <= n; i++) {
if (dp[len] < a[i]) {
dp[++len] = a[i];
}
dp[lower_bound(dp + 1, dp + len + 1, a[i]) - dp] = a[i];
s[i] = len;
}
len = 0;
for (int i = n; i >= 1; i--) {
if (dp2[len] < a[i]) {
dp2[++len] = a[i];
}
dp2[lower_bound(dp2 + 1, dp2 + len + 1, a[i]) - dp2] = a[i];
s[i] = min(s[i], len);
}
for (int i = 1; i <= n; i++) {
ans = max(ans, 2 * s[i] - 1);
}
printf("%d", ans);
return 0;
}
锦鲤保佑我拿到 Accepted
E. 烈焰
她从火光中走来,是那样璀璨夺目
这道 dp 惨遭吐槽:「这 dp 状态是正常人想的出来的吗?!」
烈焰(危)。
「我的做题历程」:
step1:观察题面。
“一维的扫雷地图” ,线性的。
“可能的情况有多少种” ,dp。
(题型:线性 dp)
step2:思考解法。
第一步思考 dp 状态:
\(dp_{i, j, k}(i \in [1, n], j \in [0, 1], k \in [0, 1])\):前 \(i\) 位里,当前第 \(i\) 位和第 \(i + 1\) 位是否有火的所有可能性,
第二步思考状态转移方程:
一共有四种可能性,\(dp(i, 0, 0),\ dp(i, 0, 1),\ dp(i, 1, 0),\ dp(i, 1, 1)\)。
然后根据题目写就好了,这里不展开。
step3:完成代码。
代码(抵制学术不端行为,拒绝 Ctrl + C):
#include <bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5, mod = 1e9 + 7;
typedef long long ll;
char s[N];
int dp[N][2][2], n;
int main() {
freopen("fire.in", "r", stdin);
freopen("fire.out", "w", stdout);
while (~scanf("%s", s + 1)) {
n = strlen(s + 1);
memset(dp, 0, sizeof dp);
dp[0][0][0] = dp[0][0][1] = 1;
for (int i = 1; i <= n; i++) {
if (s[i] == '0') {
dp[i][0][0] = dp[i - 1][0][0];
}
if (s[i] == '1') {
dp[i][0][1] = dp[i - 1][0][0];
dp[i][0][0] = dp[i - 1][1][0];
}
if (s[i] == '2') {
dp[i][0][1] = dp[i - 1][1][0];
}
if (s[i] == '*') {
dp[i][1][1] = dp[i][1][0] = (dp[i - 1][0][1] + dp[i - 1][1][1]) % mod;
}
if (s[i] == '?') {
dp[i][0][1] = dp[i][0][0] = (dp[i - 1][1][0] + dp[i - 1][0][0]) % mod;
dp[i][1][0] = dp[i][1][1] = (dp[i - 1][0][1] + dp[i - 1][1][1]) % mod;
}
}
printf("%d\n", (dp[n][1][0] + dp[n][0][0]) % mod);
}
return 0;
}
因为状态转移只牵扯到 \(i\) 和 \(i + 1\) ,于是我们还能滚动一下,快个 \(800\text{ms}\) 左右。
代码(抵制学术不端行为,拒绝 Ctrl + C):
// 滚动做法
#include <bits/stdc+
+.h>
using namespace std;
const int N = 1e6 + 5, mod = 1e9 + 7;
char s[N];
int dp[2][2][2], n;
int main() {
freopen("fire.in", "r", stdin);
freopen("fire.out", "w", stdout);
while (~scanf("%s", s + 1)) {
n = strlen(s + 1);
memset(dp, 0, sizeof dp);
dp[0][0][0] = dp[0][0][1] = 1;
for (int i = 1; i <= n; i++) {
if (s[i] == '0') {
dp[i & 1][0][0] = dp[i - 1 & 1][0][0];
dp[i & 1][1][0] = dp[i & 1][0][1] = dp[i & 1][1][1] = 0;
// 由于是滚动的所以不需要的数据无法被覆盖,需要自行清零
}
if (s[i] == '1') {
dp[i & 1][0][1] = dp[i - 1 & 1][0][0];
dp[i & 1][0][0] = dp[i - 1 & 1][1][0];
dp[i & 1][1][0] = dp[i & 1][1][1] = 0;
}
if (s[i] == '2') {
dp[i & 1][0][1] = dp[i - 1 & 1][1][0];
dp[i & 1][1][0] = dp[i & 1][0][0] = dp[i & 1][1][1] = 0;
}
if (s[i] == '*') {
dp[i & 1][1][1] = dp[i & 1][1][0] = (dp[i - 1 & 1][0][1] + dp[i - 1 & 1][1][1]) % mod;
dp[i & 1][0][0] = dp[i & 1][0][1] = 0;
}
if (s[i] == '?') {
dp[i & 1][0][1] = dp[i & 1][0][0] = (dp[i - 1 & 1][1][0] + dp[i - 1 & 1][0][0]) % mod;
dp[i & 1][1][0] = dp[i & 1][1][1] = (dp[i - 1 & 1][0][1] + dp[i - 1 & 1][1][1]) % mod;
}
}
printf("%d\n", (dp[n & 1][1][0] + dp[n & 1][0][0]) % mod);
}
return 0;
}
火中抢 Accepted
终于写完了
鸣谢 cqbzgm 提供的部分思路支持,C2024liuziming,C2024zhangwangbo,C2024liaoxindi 提供的格式指导🔆
补题完成~
将AC打包带走
将思路带包带走哦~
2022.5.14全盘题解到此结束~🎊🎊🎊
叭叭~(≧∇≦)ノ