HMM算法原理
前置知识
概率相加
若完成一件事情有很多方法，注意，每个方法都能独立完成这个事情，又每个方法都有一定的概率，那么完成这个事情的概率就用相加。
概率相乘
若完成一件事情需要N个步骤才能完成，而每一个步骤都有一定的概率（注意每个步骤只是完成这个事情的一个部分），则完成整个事情的概率用的就是相乘。
条件概率公式
全概率公式
贝叶斯公式
HMM模型的5个参数
先举个例子：现在有某地一周的天气预报，观测到的结果是，周一: Sun, 周二: Sun, 周三: Rain, 周四: Sun, 周五: Rain, 周六: Rain, 周日: Sun
假设我们知道某地以往所有的天气，那我们就可以统计出Sun的天数，Rain的天数，Cloud的天数，然后计算出Sun的初始化概率，Rain的初始化概率，Cloud的初始化概率以及这三个状态之间的转移概率。假设统计出的结果如下：
Sun的初始化概率 = 0.6，Rain的初始化概率 = 0.2， Cloud的初始化概率 = 0.2，状态转移矩阵为
sun rain cloud
sun 0.6 0.1 0.3
rain 0.1 0.7 0.2
cloud 0.3 0.3 0.4
那么我们就可以很轻松地求出这一周天气为周一: Sun, 周二: Sun, 周三: Rain, 周四: Sun, 周五: Rain, 周六: Rain, 周日: Sun的发生概率。
但是突然有一天，你被关进了一个小黑屋，你不能直接知道外面的天气，你只能看看小屋子里面苔藓的干湿情况，并且你知道天气能影响苔藓的干湿情况。那么现在如果你想了解天气情况以及相关的信息，你该怎么办？这就是HMM算法需要做的事。
这里先解释下HMM模型出现的5个参数，以及各自代表的含义
- S：隐藏状态的集合（Sun, Cloud, Rain），N为隐状态个数 N = 3
- K: 输出状态或者说观测状态的集合（Soggy, Damp, Dryish, Dry），M为观测状态个数M = 4
- π: 对应隐藏状态的初始化概率 （sun : 0.6, cloud : 0.2, rain : 0.2）
- A: 隐藏状态的状态转移概率，是一个
N*N的概率矩阵，就是上面所列举出来的矩阵。 - B: 隐藏状态到观测状态的混淆矩阵，是一个
N*M的发射概率矩阵
HMM模型需要解决的三个问题
观测序列发生的概率
给定观测序列O(o1,o2,…,oT)和模型μ = (π,A,B),求出P(O|u),即给定模型下观测序列发生的概率是多少？
前向算法
基本思想：定义前向变量αt(i)：表示观测序列是O1, O2, ..., Ot，且t时刻的隐藏状态是Si的概率，其公式表示如下
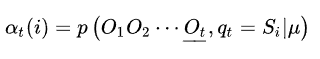
通俗地讲，就是我现在观测到了这个观测序列，并且知道在t时刻是由隐藏状态Si观测到的。
上面定义有限定了两个条件， 一个是截止到t时刻的观测序列是O1, O2, ..., Ot；另一个是t时刻的隐藏状态是Si。举个例子说明前向变量的作用。
HMM参数以下图为例：
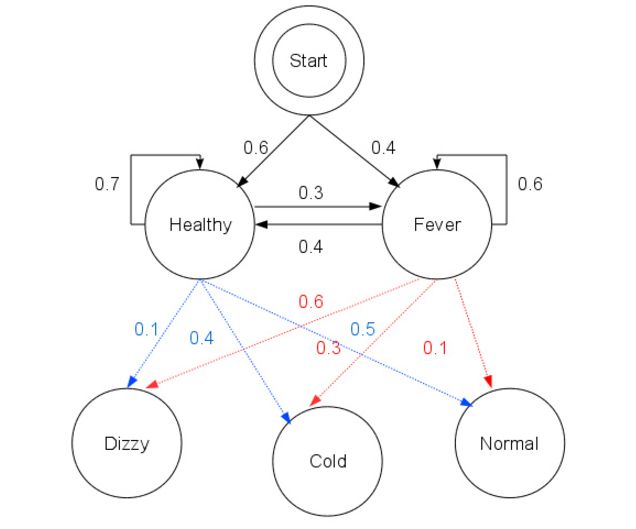
假设现在要求第二天(t = 2)出现观测序列是(Dizzy, Cold)的概率是多少？
因为总共有两个隐藏条件，所以就需要求出α2(Fever)，即截止到第二天(t=2)的观测序列是(Dizzy, Cold)，且第二天的隐藏状态是Fever的概率，和α2(Healthy)，即截止到第二天(t=2)的观测序列是(Dizzy, Cold)，且第二天的隐藏状态是Healthy的概率，最后把这两个概率加起来(α2(Fever) + α2(Healthy))就是最终的结果。因为由每一个隐藏状态都可能映射到相同的观测状态，把所有可能的概率加起来就是最终的概率。
因此，如果可以高效地计算αt(i)，就可以高效地计算P(O|μ)。
前向算法公式推导
参考博客：https://zhuanlan.zhihu.com/p/85454896
里面用到了全概率公式和条件概率公式
前向算法代码实现
# 状态转移矩阵
self.A = array([(0.5, 0.2, 0.3), (0.3, 0.5, 0.2), (0.2, 0.3, 0.5)])
# 发射概率矩阵，其shape为 隐藏状态个数*观测状态个数 = 3 * 2
self.B = array([(0.5, 0.5), (0.4, 0.6), (0.7, 0.3)])
# 隐藏状态的初始化概率
self.pi = array([(0.2), (0.4), (0.4)])
# 观测状态序列，观测状态只有两种：0和1。
self.o = [0, 1, 0]
self.t = len(self.o) # 观测序列长度
self.m = len(self.A) # 状态集合个数
self.n = len(self.B[0]) # 观测集合个数
求解问题：通过前向算法求得观测序列[0, 1, 0]发生的概率
def forward(self):
# α矩阵大小行数为观测序列数，列数为状态个数
self.x = array(zeros((self.t, self.m)))
# 先计算出t1时刻，观测状态为0的概率
for i in range(self.m):
# 用每一个隐藏状态的初始化概率 * 发射概率矩阵中该隐藏状态下能观察到观察状态0的概率
self.x[0][i] = self.pi[i] * self.B[i][self.o[0]]
# 计算其他时刻每一个隐藏状态下观测到当前时刻的观测值的概率
for j in range(1, self.t):
for i in range(self.m):
# 前一时刻所有状态的概率乘以转移概率得到i状态概率
# i状态的概率*i状态到j观测的概率
temp = 0
for k in range(self.m):
temp = temp + self.x[j - 1][k] * self.A[k][i]
self.x[j][i] = temp * self.B[i][self.o[j]]
result = 0
for i in range(self.m):
result = result + self.x[self.t - 1][i]
print(u"前向概率矩阵及当前观测序列概率如下：")
print(self.x)
print(result)
概率最大的隐藏状态序列
解决的问题：利用模型和观测序列找出最优的隐藏状态序列
参考博客：https://blog.csdn.net/shenxiaoming77/article/details/79228378
实现代码：
def viterbi(self):
# 利用模型和观测序列找出最优的隐藏状态序列
# 每个路径都有自己的概率，最大的概率用矩阵z记录,前一个状态用d矩阵记录
self.z = array(zeros((self.t, self.m)))
self.d = array(zeros((self.t, self.m)))
for i in range(self.m):
self.z[0][i] = self.pi[i] * self.B[i][self.o[0]]
self.d[0][i] = 0
for j in range(1, self.t):
for i in range(self.m):
maxnum = self.z[j - 1][0] * self.A[0][i]
node = 1
for k in range(1, self.m):
temp = self.z[j - 1][k] * self.A[k][i]
if maxnum < temp:
maxnum = temp
node = k + 1
self.z[j][i] = maxnum * self.B[i][self.o[j]]
self.d[j][i] = node
# 找到T时刻概率最大的路径
max_probability = self.z[self.t - 1][0]
last_node = [1]
temp = 0
for i in range(1, self.m):
if max_probability < self.z[self.t - 1][i]:
max_probability = self.z[self.t - 1][i]
last_node[0] = i + 1
temp = i
i = self.t - 1
# self.d[t][p],t时刻状态为p的时候，t-1时刻的状态
while i >= 1:
last_node.append(self.d[i][temp])
i = i - 1
temp = ['o']
temp[0] = int(last_node[len(last_node) - 1])
j = len(last_node) - 2
while j >= 0:
temp.append(int(last_node[j]))
j = j - 1
print(u'路径节点分别为')
print(temp)
print(u'该路径概率为' + str(max_probability))
