【ML代码从零开始实现 - python】回归——线性回归、逻辑斯蒂回归、感知机、最大熵模型

线性回归、逻辑斯帝回归

import numpy as np
import matplotlib.pyplot as plt
from random import random

def sigmond(x):
    return 1 / (1 + np.exp(-x))

def log_cly(p):
    if p >= 0.5:
        return 1
    else:
        return 0

class Regression():
    def __init__(self, learning_rate, max_iter):
        assert learning_rate > 0
        assert learning_rate < 1
        assert isinstance(max_iter, int)

        self.learning_rate = learning_rate
        self.max_iter = max_iter

        super(Regression, self).__init__()

    def fit(self, X, y):
        num_samples = len(X)
        num_features = (X.shape)[1]

        assert len(X) == len(y)

        self.w = np.random.random(num_features)
        self.b = 0

        for i in range(self.max_iter):
            self.w += np.array(self.learning_rate * sum([(yi - self.predict_sample(xi)) * xi 
                               for xi, yi in zip(X, y)])) / num_samples
            self.b += np.array(self.learning_rate * sum([(yi - self.predict_sample(xi)) 
                               for xi, yi in zip(X, y)])) / num_samples
            '''
            l = self.loss(X, y)
            if (i+1) % 100 == 0:
                print("epoch: {0}, loss: {1}".format(i + 1, l))
            '''

    def predict(self, X):
        return [self.predict_sample(xi) for xi in X]

    def predict_sample(self, xi):
        pass

    def loss(self, X, y):
        pass


class LinearRegression(Regression):
    def __init__(self, learning_rate, max_iter):
        super(LinearRegression, self).__init__(learning_rate, max_iter)

    def predict_sample(self, xi):
        return sum(self.w * np.array(xi)) + self.b

    def loss(self, X, y):
        y_pred = np.array([self.predict_sample(xi) for xi in X])
        return sum((y_pred-y) * (y_pred-y))


class LogisticRegression(Regression):
    def __init__(self, learning_rate, max_iter):
        super(LogisticRegression, self).__init__(learning_rate, max_iter)

    def predict_sample(self, xi):
        return sigmond(sum(self.w * np.array(xi)) + self.b)

    def predict_class(self, X):
        y_pred_prob = self.predict(X)
        pred_class = [log_cly(pi) for pi in y_pred_prob]
        return pred_class

    def loss(self, X, y):
        y_pred = [self.predict_sample(xi) for xi in X]
        cross_entropy = -np.array([(yi * np.log(yi_pred) + (1-yi) * np.log(yi_pred)) 
                                   for yi, yi_pred in zip(y, y_pred)])
        return sum(cross_entropy)


# a simple test of linear regression
'''
def create_data(true_w, true_b, num_examples):
    features = np.random.random((num_examples, len(true_w)))
    labels = np.array([sum(fi * true_w) + true_b for fi in features]) + np.random.random() * 0.1
    return features, labels

true_w = [4.2, -2.0, 1.5]
true_b = [1.0]
features, labels = create_data(true_w, true_b, 1000)

LinReg = LinearRegression(0.03, 2000)
LinReg.fit(features, labels)
'''

# a simple test of logistic regression
'''
def create_data(true_w, true_b, num_examples):
    features = np.random.random((num_examples, len(true_w)))
    probs = np.array([sum(fi * true_w) + true_b for fi in features]) + np.random.random() * 0.1
    return features, probs

def create_labels(probs):
    return np.array([log_cly(pi) for pi in probs])

true_w = [4.2, -2.0, 1.5]
true_b = [1.0]
features, probs = create_data(true_w, true_b, 1000)
labels = create_labels(probs)

LogReg = LogisticRegression(0.03, 2000)
LogReg.fit(features, labels)
'''

 

线性回归测试：

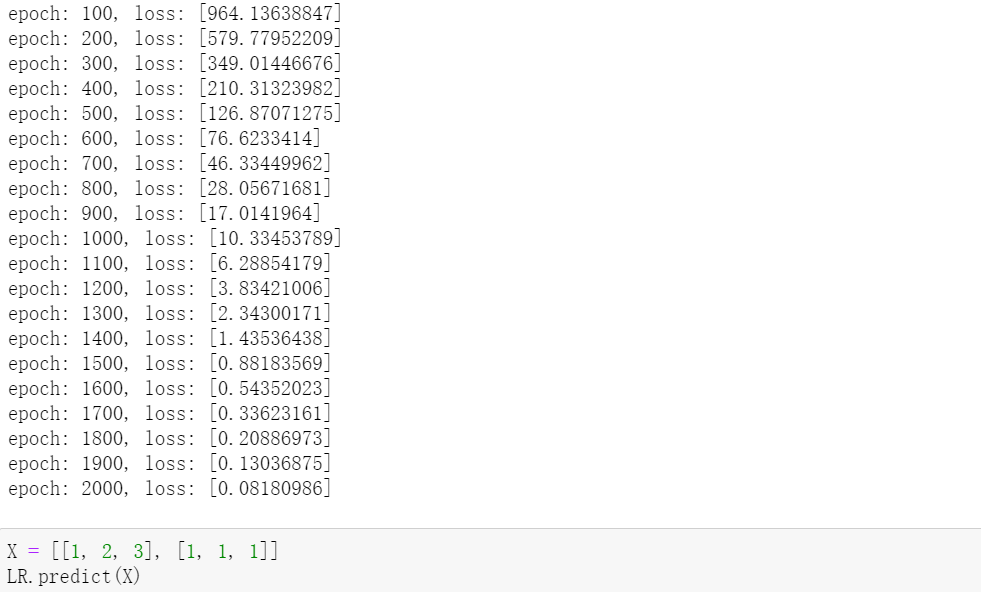
 逻辑斯蒂回归测试：

 

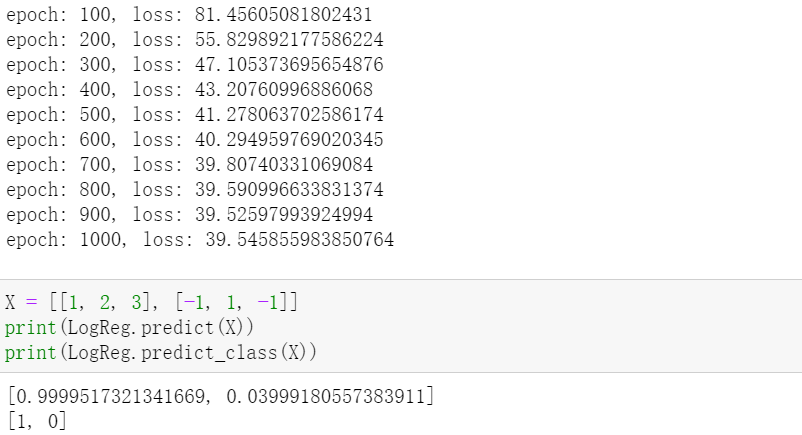
感知机

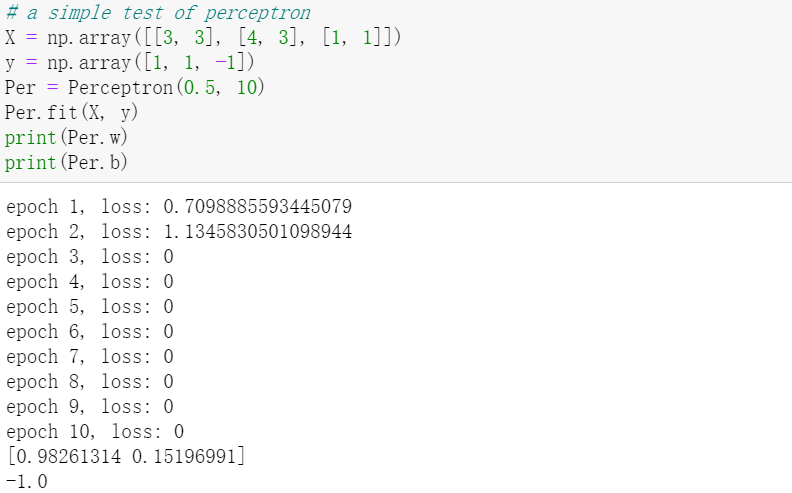
def sign(x):
    if x >= 0:
        return 1
    else:
        return -1

class Perceptron():
    def __init__(self, learning_rate, max_iter):
        assert learning_rate > 0
        assert learning_rate < 1
        assert isinstance(max_iter, int)

        self.learning_rate = learning_rate
        self.max_iter = max_iter

        super(Perceptron, self).__init__()

    def fit(self, X, y):
        num_samples = len(X)
        num_features = (X.shape)[1]

        assert len(X) == len(y)

        self.w = np.random.random(num_features)
        self.b = 0

        for i in range(self.max_iter):
            for xi, yi in zip(X, y):
                if (yi * (sum(self.w * np.array(xi) + self.b)) < 0):
                    self.w += self.learning_rate * yi * np.array(xi)
                    self.b += self.learning_rate * yi
            l = self.loss(X, y)
            print("epoch {0}, loss: {1}".format(i+1, l))

    def predict(self, X):
        return [self.predict_sample(xi) for xi in range(X)]

    def predict_sample(self, xi):
        return sign(self.w * np.array(xi) + self.b)

    def loss(self, X, y):
        loss_sample = []
        for xi, yi in zip(X, y):
            if (yi * (sum(self.w * np.array(xi) + self.b)) < 0):
                loss_sample.append(-yi * (sum(self.w * np.array(xi) + self.b)))
        return sum(loss_sample)


# a simple test of perceptron
'''
X = np.array([[3, 3], [4, 3], [1, 1]])
y = np.array([1, 1, -1])
Per = Perceptron(0.5, 10)
Per.fit(X, y)
print(Per.w)
print(Per.b)
'''

简单的例子：