【Stanford - Speech and Language Processing 读书笔记 】3、N-gram Language Models

1、Introduction

语言模型：为一个序列的词分配概率——从前几个词预测后面可能出现的词

语言模型应用广泛——在嘈杂环境下的语音识别、句法语法纠错……

最简单的语言模型——N-gram模型！

 

 

2、N-gram

从一个简单的任务，预测P(w|h)开始。 h是先前的词语序列，根据h我们需要预测h后面出现w的概率。

例如h是“The water is so transparent that”，w 是the。那么我们想知道：

                        

 

 一种计算方法是：

                     

 

然而这种方法并不是总是奏效，特别是语料库并不是足够大的时候。因为语言的可扩展性和复杂性，很多句子语料库是没有的，例如“The Yellow River' water is so transparent that”。

 为了解决这个问题，我们运用链式法则：

                      

 

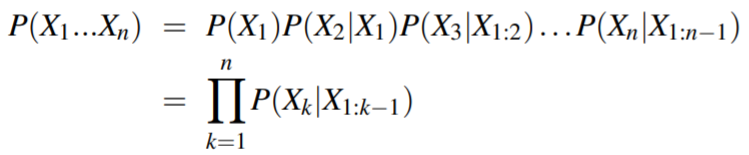
 我们可以对这个式子做一个简化和近似——马尔科夫假设（Markov assumption），即近似为后一个单词的出现仅仅与前一个单词有关：

                    

 

 在这个例子中就是计算P(the|that)。 那么，一个序列出现的概率为：

                     

 

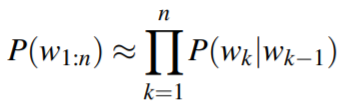
 这就是二元模型（bigram model）。

 

一个问题出现了，如何去计算P(wk|wk-1)呢？ 这里，我们使用极大似然估计法（maximum likelihood estimation），即已知结果，反推参数，使得该参数给定模型下观测结果出现的概率最大。 例如在一个100000个词的语料库中，Chinese这个词出现的次数为400， 那么我们就可以估计Chinese出现的概率最有可能是400/100000。

于是可以计算P(wk|wk-1)：

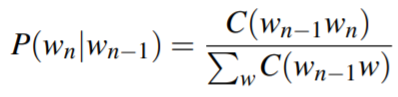           可以简化为：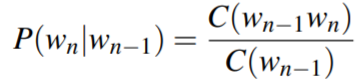 

 

实际角度的建议

1、当语料库比较充足时，trigram model、4-gram model、5-gram model的预测效果往往更好。

这些模型统称为 n-gram模型，即通过前n的词预测后一个词的概率。

2、常常使用对数概率替换概率直接相乘积：防止数值下溢

                 

 

 

 

来看一个简单的例子：

伯克利餐馆语料库统计了顾客的询问，例如：

                 

 

 截取一小部分二元统计的结果（经过规范化后）：

                

 

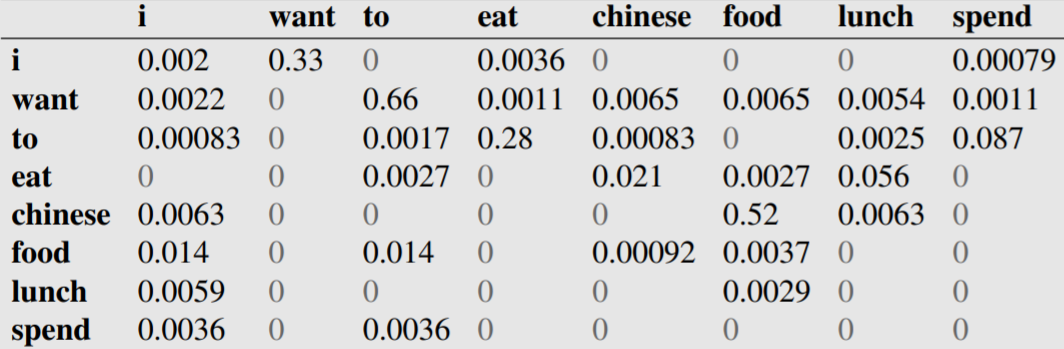
那么可以计算“i want to eat english food”的概率：

              

 

             

 

 

3、Evaluating Language Models

外在评估（extrinsic evaluate）: 端到端的评估，将训练的模型直接放到实际运用中去检验。这是判断模型是否有改进的唯一办法，但经常因为成本太高而不适用。

内在评估（intrinsic evaluate）：独立于实际运用的衡量方法，一般需要一个测试集。测试集必须独立于训练集之外，否则会导致测试的分数过高。

 

如果频繁地使用一个特定的测试集，可能不经意的会使测试集的某些性质发生改变。

为解决这一问题，可以将数据集分为训练集（training set）、开发集（dev-set）、测试集（test set）

训练集用来训练模型，开发集用来选择超参数，测试集用来测试模型

 

复杂度

复杂度（perplexity）用在测试集上，是测试结果的逆概率。

              

 

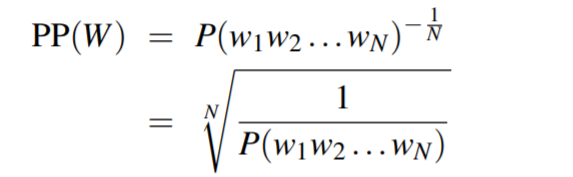
 其中PP是perplex的简写。使用链式法则：

             

 

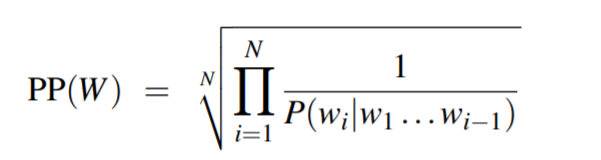
当然，上式可以用n-gram模型简化。  

 

对上面的语料库，分别用PP测试unigram、bi-gram、tri-gram、4-gram模型，可以发现PP值是递减的。

 

 

4、Generalization and Zeros

虽然对于n-gram模型，随着n值的增加，模型的效果往往越好，但是也会出现很多问题——

1、随着n的增加，n个连续的词组成的串可能的组合结果呈现指数的增长趋势，这表明所有字串在语料库中出现数量构成的向量是稀疏的（sparse）。

2、由于语言的复杂性，在语料库中可能会出现未知的词语（unknow words）。

 

一方面，如果某个词串出现在测试集但是不出现在训练集，这表明我们低估了它出现的可能性，这将减低模型在运行数据上的表现；

另一方面，如果该词串出现在训练集但是不出现在测试集，我们将无法计算perplexity！

 

对于未知词语的问题。可以采用<UNK>模型，有两种方法来训练该模型：

1、先预先给定一个固定的词汇库， 对于未知的词语，将其统一记为<UNK>，最后统计<UNK>出现的次数计算概率。

2、没有预先给定的词汇库，而是把训练集中出现个数小于n的词置为<UNK>，或者将训练集出现次数从大到小前V个以外的单词置为<UNK>

 

 

5、Smoothing

我们如何处理词汇表中的单词（它们不是未知单词）但出现在测试集中的未知上下文中（例如，它们出现在训练中从未出现过的单词之后）？

防止语言模型分配这些看不见的事件的概率为零，我们必须削减一点概率，从一些更频繁的事件中获取大量信息，并将其赋予我们从未见过的事件。

这中方法称为平滑（Smoothing），以下介绍几种平滑方法：Laplace (add-one) smoothing,  add-k smoothing, stupid backoff,  Kneser-Ney smoothing.

 

Laplace Smoothing

计算概率时分子分母同时加1：

        

 

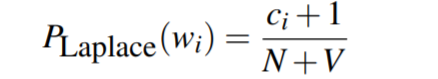
 例如unigram模型：

            

 

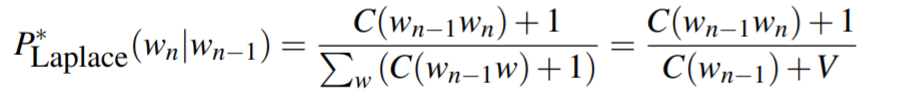
Add-k Smoothing

计算概率时分子分母同时加k：

          

 

 

Backoff and Interpolation

回退(Backoff)：例如计算但是没有的实例时，可以用代替，如果计算仍然没有实例的话，则一直回退下去。

 

插值（Interpolation）: n-gram的模型可以用n-gram，(n-1)-gram......unigram的加权混合表示。例如：

         

 

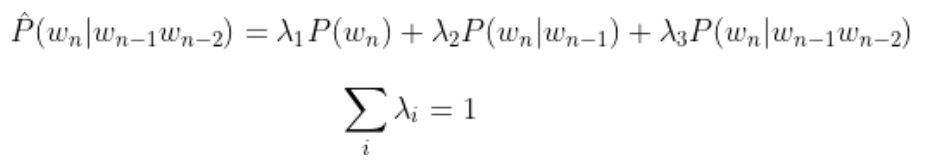
 插值的计算可以更精确一些：

         

 

在一个额外的语料库中，利用极大似然语料库的概率计算lambda函数，一般采用EM算法计算。