【线性代数】正交向量和正交子空间

正交向量

正交（orthogonal）：垂直

                              

 

                           

 

 

正交子空间

子空间S和子空间T正交：S中每个向量与T中每个向量正交

矩阵A的行空间和A的零空间正交，且形成一对正交补（零空间包含所有垂直于行空间的向量）：

                               

简证：

                             

 

 对上述n个式子累和即证。

 同理， 列空间和左零空间正交

 

求解Ax = b（无解情况）

                          

 

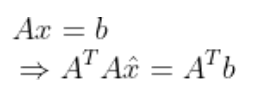
 A^T A 为对称的方阵，有如下性质：

                         

 

A^T A可逆 等价于 A各列线性无关。