【线性代数】矩阵空间、秩一矩阵和最小世界图

矩阵空间

所有m*n矩阵组成的集合是一个向量空间，因为其加法和乘法封闭（在这里我们不需要考虑矩阵乘法）

满足这种加法和数乘条件的都可以是向量空间（不必约束于“向量”二字），例如：

                            

 

其解构成一个向量空间，它的一组基为：

                           

 

 

向量空间的和

两个向量空间S和U，S与U的交为向量空间，而S与U的并不一定是向量空间。

定义向量的和：

                             

S+U为向量空间。同时有：

                            

 

 

秩一矩阵

对于秩为一的矩阵A，可以表示成一个行向量和列向量的乘积：

                           

 

例如：

                         

 

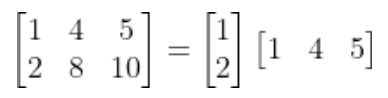
 诸如这种秩一矩阵可以搭建任何矩阵，一个秩为二的矩阵可以由几个秩为一的矩阵乘积得到。

对于秩一矩阵A，dim N(A) = n-1

 

相同秩的矩阵未必能够组成子空间。

 

最小世界图

Graph = { nodes, edges}

最小世界图——“六度分离猜想”