【线性代数】 矩阵的乘法和逆

矩阵乘法

A * B = C     A，B，C为矩阵，则必须满足形状A：m*n，n*k,  m*k——A的列数等于B的行数，C的行数等于A的行数，C的列数等于B的列数

则矩阵的乘法定义为：

 

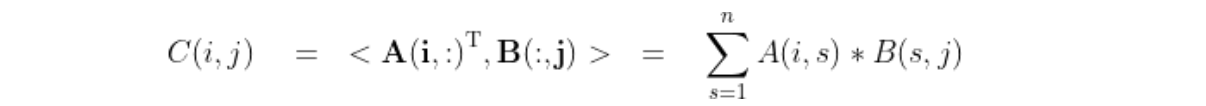
 矩阵C中第i行第j列元素C(i,j)为A中第i行和B中第j列对应元素的乘积的和。

 

注意：矩阵乘法结合律成立，交换律不成立

 

矩阵的乘法对分块矩阵也适用

分块矩阵简介：一个分块矩阵(分段矩阵)就是将矩阵分割出较小的矩形矩阵，这些较小的矩阵就称为区块。换个方式来说，就是以较小的矩阵组合成一个矩阵。通过将大的矩阵通过分块的方式划分，并将每个分块(称为子块)看做另一个矩阵的元素，这样之后再参与运算，通常可以简化运算。例如，有的大矩阵可以通过分块变为对角矩阵或者是三角矩阵等特殊形式的矩阵。分块矩阵的分割原则是以水平线和垂直线进行划分:

                           

 

 

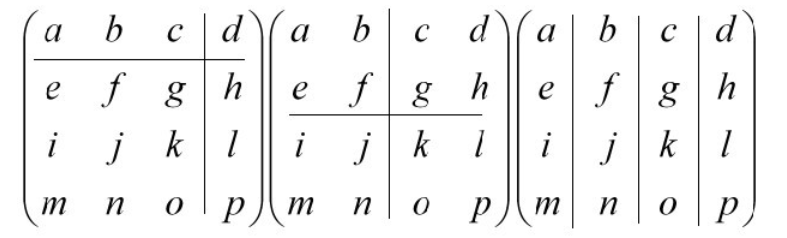
(2)分块矩阵的运算法则：

(i)对于加法,数乘,矩阵乘法就是对每个子块执行对应的操作

(ii)对于加法要注意分块的时候要确保对应子块的行列数要相同也就是要用相同的方法分块.

设矩阵A和B的行列数相同，并采用相同的分块法分成：

                        

 

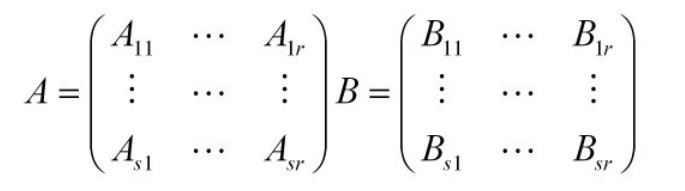
 (iii)对于矩阵乘法要注意对应子块要确保相乘是有意义的（第一个子块的列数等于第二个的行数）

                       

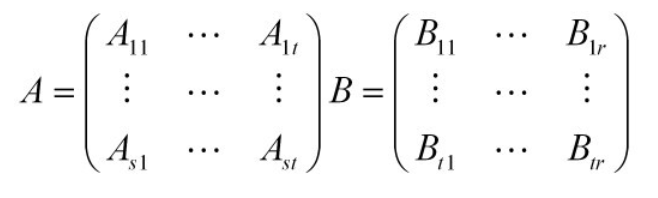
设A为m × l矩阵 , B为l × n矩阵 ,分块成：

 

 若A的子块的列数等于B对应子块的行数则：

                     

 

 

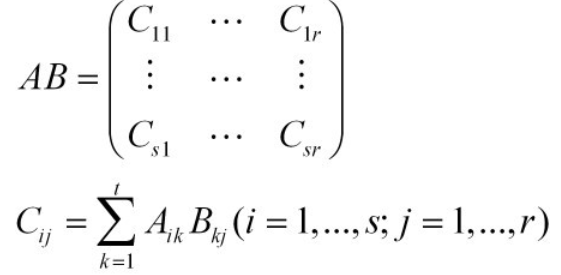
矩阵的逆

方阵A的逆A^{-1}满足如下等式：

                               

 

矩阵可逆当且仅当以下两个条件满足其一：

（1）行列式不为0 （行列式后续深入介绍）

（2） 不存在非零向量x，使得Ax = 0

 

（2）的理解：若存在Ax = 0且A可逆，则：

                              

 

      矛盾！ 事实上（2）可以从线性无关角度解释， 从这个角度看（1）和（2）是等价的

 

矩阵求逆——高斯-若尔当

矩阵A乘逆矩阵的第j列为单位阵的第j列

                                  

将矩阵A和单位阵I的列拼接（看成增广矩阵），沿用求解线性方程组的做法，化为行最简形矩阵，得到A的逆：

                            

 

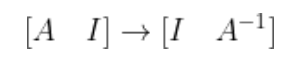
解释: