《DSP using MATLAB》Problem 3.13(scilab脚本)
由P3.12的结论可知,将正弦(余弦)信号输入一个LTI(线性时不变)系统,那么其输出仍是同频率的正弦(余弦)信号,但模和相位都经过系统的修正,修正的系数跟
系统的频率响应函数(脉冲响应序列的DTFT)在该频率的值有关。

一、计算LTI系统的幅度谱和相位谱
已经给出了系统的脉冲响应序列,计算其离散时间傅里叶变换(DTFT)即可。
有两大类方法:
1、公式定义类
注意,定义中n是无限长,从-∞到+∞。


利用上图中最后的两个公式,就得到方法一、方法二。
2、实际数值计算类(MATLAB或scilab实现)
计算机计算不了无限的东西,只能取有限长序列。



利用书中的3.4式子定义,得到方法三、方法四。
二、代码

1 // Book Author:Vinay K Ingle, John G Proakis 2 // 3 // Problem 3.13 4 // script by: KY 5 // 6 clear, clc, clf(); 7 8 mode(2); 9 funcprot(0); 10 load('../fun/lib'); 11 12 // ----------------------------------------------------------------------------- 13 // START Output Info about this sce-file 14 mprintf('\n***********************************************************\n'); 15 [ban1,ban2] = fun_banner(); 16 mprintf("\n <DSP using MATLAB> 3rd edition, Problem 3.13.1 \n"); 17 mprintf(" ----------------------------------------------------------\n\n"); 18 19 // ----------------END---------------------------------------------------------- 20 21 //% ------------------------------------------------------------------ 22 //% h1(n) 23 //% ------------------------------------------------------------------ 24 //M = 10; 25 //M = 15; 26 //M = 25; 27 M = 50; 28 29 n1_start = -M; n1_end = M; 30 n1 = [n1_start : n1_end - 1]; 31 32 x1 = 0.9 .^ abs(n1); 33 34 // ----------------------------------------------------------------------------- 35 // --------------------START f0 figure----------------------------------------- 36 f0=scf(0); //creates figure with id==0 and make it the current one 37 f0.figure_size=[1000,700]; // adjust window size 38 f0.background=8; // add background color 8-white 39 f0.figure_name=msprintf("Fig0 Problem 3.13.1 h1(n), M = %d",M); // name window 40 41 plot(n1,x1,'bo'); 42 plot(n1,x1,'b.'); 43 plot2d3(n1,x1,2); // Create plot with blue line 44 //title("$x1(n)\ sequence\ Rectangle, M = 100$",'fontname',7,'fontsize',4); 45 title(msprintf('h1(n) sequence, M = %d', M)); 46 xlabel('$n$','fontname',3); ylabel('h1','fontname',3,'fontsize',3); 47 xgrid(5,0,7); // color, thickness, style 48 a0=get("current_axes"); // get the handle of the newly created axes 49 //a0.data_bounds=[-4,6,-6,6]; 50 // ----------------------------------------------------------------------------- 51 // --------------------END f0 ------------------------------------------------- 52 53 54 MM = 500; 55 k = [-MM:MM]; // [-pi, pi] 56 //k = [0:M]; // [0, pi] 57 w = (%pi/MM) * k; 58 59 w0_1 = 0.5 * %pi; 60 w0_2 = 0.3 * %pi; 61 theta0_1 = 60/180 * %pi; 62 63 64 //[X1] = fun_dtft(x1, n1, w); // method #3 65 [X1, w] = fun_dtft1(x1, n1, MM); // method #4 66 //X1 = ( 2*ones(1, length(w)) - 0.9*exp(%i*w) - 0.9*exp(-%i*w)) ./ ( (1-0.9*exp(-%i*w)) .* (1-0.9*exp(%i*w))); // method #1 67 //X1 = ( 2 * ones(1, length(w)) - 1.8*cos(w)) ./ ( 1.81*ones(1, length(w)) - 1.8*cos(w)); // method #2 68 69 magX1 = abs(X1); angX1 = fun_angle(X1); realX1 = real(X1); imagX1 = imag(X1); 70 71 mprintf('w0 = %.2fpi, magX1_w0 = %.4f, angX1_w0 = %.4f \n', w0_1/%pi, magX1(find(k/MM==0.5)), angX1(find(k/MM==0.5))); 72 mprintf('w0 = %.2fpi, magX1_w0 = %.4f, angX1_w0 = %.4f \n', w0_2/%pi, magX1(find(k/MM==0.3)), angX1(find(k/MM==0.3))); 73 74 //%% --------------------------------------------------------------------------- 75 //%% START X(w)'s mag ang real imag 76 // --------------------START f1 figure----------------------------------------- 77 f1=scf(1); //creates figure with id==0 and make it the current one 78 f1.figure_size=[1000,700]; // adjust window size 79 f1.background=8; // add background color 8-white 80 f1.figure_name=msprintf("Fig1 Problem 3.13.1 DTFT of h1(n), M = %d",M); // name window 81 subplot(2, 2, 1); 82 plot(w/%pi,magX1); 83 title("$Magnitude\ Response$",'fontname',7,'fontsize',4); 84 xlabel('$frequency\ in\ \pi\ units$','fontname',3); ylabel('Magnitude |X|','fontname',3,'fontsize',3); 85 xgrid(5,0,7); // color, thickness, style 86 a0=get("current_axes"); // get the handle of the newly created axes 87 //a0.data_bounds=[-4,6,-6,6]; 88 89 subplot(2, 2, 3); 90 plot(w/%pi,angX1/%pi); 91 title("$Phase\ Response$",'fontname',7,'fontsize',4); 92 xlabel('$frequency\ in\ \pi\ units$','fontname',3); ylabel('$Radians/\pi$','fontname',3,'fontsize',3); 93 xgrid(5,1,7); // color, thickness, style 94 a1=get("current_axes"); // get the handle of the newly created axes 95 //a1.data_bounds=[-4,6,-2,2]; 96 97 subplot(2, 2, 2); 98 plot(w/%pi,realX1); 99 title("$Real\ Part$",'fontname',7,'fontsize',4); 100 xlabel('$frequency\ in\ \pi\ units$','fontname',3); ylabel('Real','fontname',3,'fontsize',3); 101 //xgrid(); 102 xgrid(5,1,7); // color, thickness, style 103 a2=get("current_axes"); // get the handle of the newly created axes 104 //a2.data_bounds=[-4,6,-2,2]; 105 106 subplot(2, 2, 4); 107 plot(w/%pi,imagX1*exp(0)); 108 title("$Imaginary\ Part$",'fontname',7,'fontsize',4); 109 xlabel('$frequency\ in\ \pi\ units$','fontname',3); ylabel('Imaginary','fontname',3,'fontsize',3); 110 //xgrid(); 111 xgrid(5,1,7); // color, thickness, style 112 a3=get("current_axes"); // get the handle of the newly created axes 113 //a2.data_bounds=[-4,6,-2,2]; 114 // ----------------------------END f1------------------------------------------- 115 //%% END X(w)'s mag ang real imag 116 //%% ---------------------------------------------------------------------------
三、运行结果
1、脉冲响应序列,长度设为101

2、使用公式定义计算频谱(脉冲响应序列的DTFT)

3、下面是按照第一部分介绍的4种方法,分别计算频谱,然后在与输入函数相同频率处,取得频谱(频率响应函数)对应的值。
①方法一
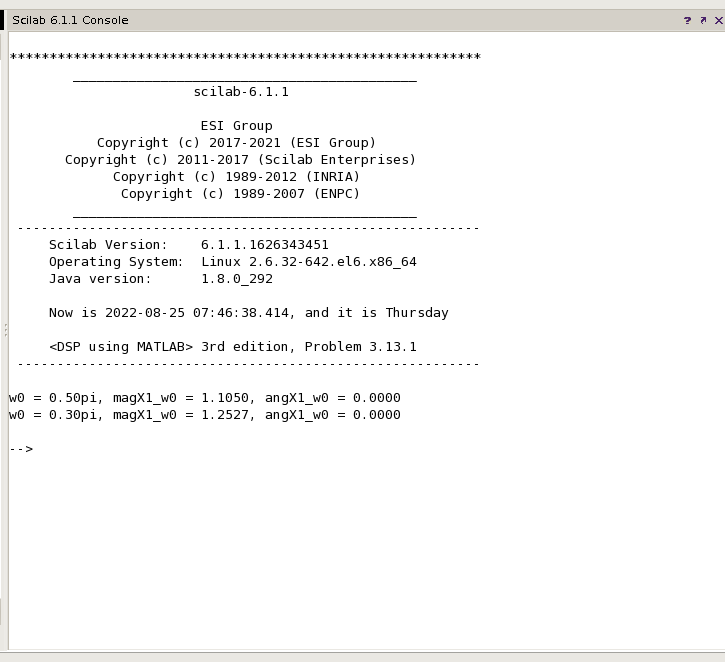
②方法二
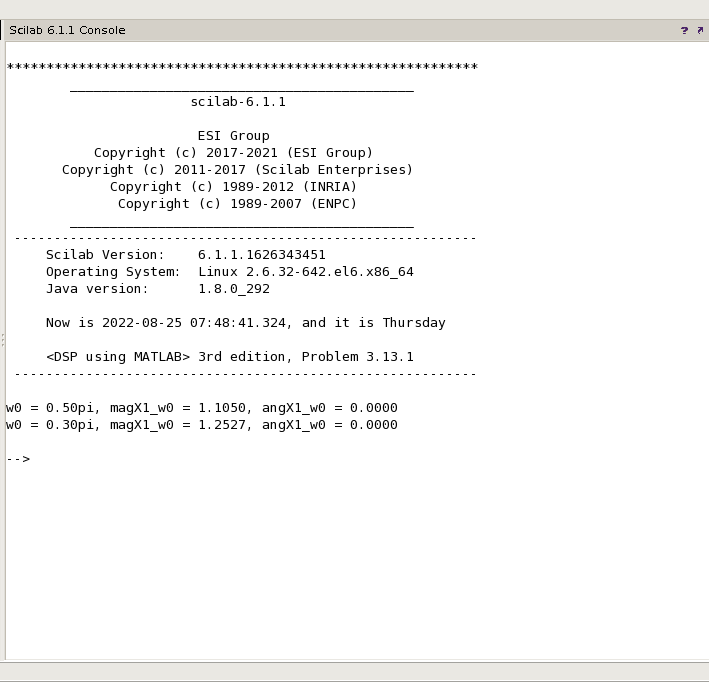
③方法三
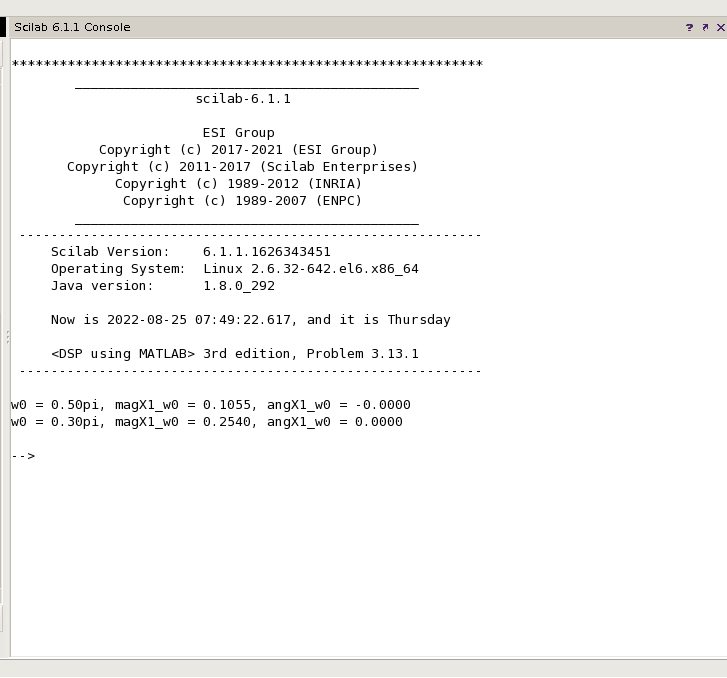
④方法四

因为特定角频率处相位谱的值为零,故只将幅度谱的值列表总结见下表,可见,利用公式定义得到的结果是最准确的,
而利用Problem 3.1的方法得到的结果稍有误差,也就是书中所说这种计算DTFT的方法并不是最有效的(not the most elegant way)。
| 0.5π | 0.3π | |
| 1 | 1.1050 | 1.2527 |
| 2 | 1.1050 | 1.2527 |
| 3 | 0.1055 | 0.2540 |
| 4 | 0.1055 | 0.0666 |
*****文中不对的地方欢迎批评指正*****
牢记:
1、如果你决定做某事,那就动手去做;不要受任何人、任何事的干扰。2、这个世界并不完美,但依然值得我们去为之奋斗。








【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· winform 绘制太阳,地球,月球 运作规律
· AI与.NET技术实操系列(五):向量存储与相似性搜索在 .NET 中的实现
· 超详细:普通电脑也行Windows部署deepseek R1训练数据并当服务器共享给他人
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 上周热点回顾(3.3-3.9)