20182327 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结
2019-11-27 19:46 BBIowa 阅读(176) 评论(0) 编辑 收藏 举报20182327 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结
教材学习内容总结
-
1、 无向图:与树类似,图也由结点和这些结点之间的连接构成。这些结点是顶点,而结点之间的链接是边。无向图是一种边为无序结点对的图。于是,记做(A,B)的边就意味着A与B之间有一条从两个方向都可以游历的连接。边记作(A,B)和记作(B,A)的含义是完全一样的。
如果图中的两个顶点之间有一条连通边,则称这两个顶点是邻接的。邻接顶点有时也称为邻居。
联通一个顶点及其自身的边称为自循环或环。 -
2、完全图:如果一个无向图含有最多条边,那么它为完全图。完全图有n(n-1)条边。(此时假设没有边自循环。)
连接图中两个顶点的边的序列,可以由多条边组成。(图中的路径是双向的。)
路径长度:路径中所含边的数目(顶点个数减1)。
连通图:无向图中任意两个顶点之间都存在一条路径。(完全图一定是连通图,连通图不一定是完全图。) -
3、有向图:又称双向图,是一种边为有序顶点对的图。(边(A,B)和边(B,A)方向不同)
有向路径:连接两个顶点有向边的序列。不存在其他顶点到树根的连接。
每个非树根元素恰好有一个连接。
树根到每个其他顶点都有一条路径。 -
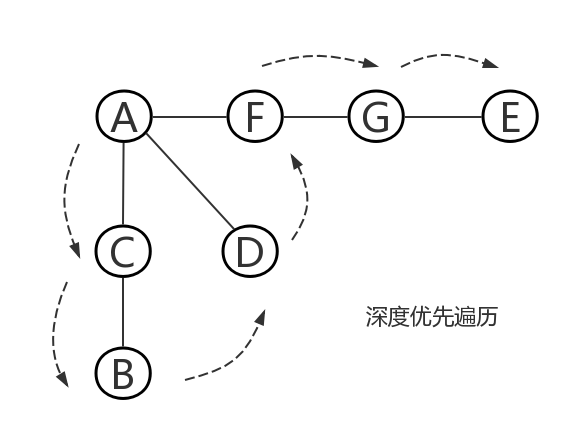
4、深度优先遍历:和树的先序遍历比较类似。假设初始状态是图中所有顶点均未被访问,则从某个顶点v出发,首先访问该顶点,然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图,直至图中所有和v有路径相通的顶点都被访问到。 若此时尚有其他顶点未被访问到,则另选一个未被访问的顶点作起始点,重复上述过程,直至图中所有顶点都被访问到为止。
-
-
①访问A。
②访问(A的邻接点)C。在第1步访问A之后,接下来应该访问的是A的邻接点,即"C,D,F"中的一个。但在本文的实现中,顶点ABCDEFG是按照顺序存储,C在"D和F"的前面,因此,先访问C。
③访问(C的邻接点)B。
在第2步访问C之后,接下来应该访问C的邻接点,即"B和D"中一个(A已经被访问过,就不算在内)。而由于B在D之前,先访问B。
④访问(C的邻接点)D。在第3步访问了C的邻接点B之后,B没有未被访问的邻接点;因此,返回到访问C的另一个邻接点D。
⑤访问(A的邻接点)F。前面已经访问了A,并且访问完了"A的邻接点B的所有邻接点(包括递归的邻接点在内)";因此,此时返回到访问A的另一个邻接点F。
⑥访问(F的邻接点)G。
⑦访问(G的邻接点)E。
因此访问顺序是:A -> C -> B -> D -> F -> G -> E -
5、广度优先遍历:
-
-
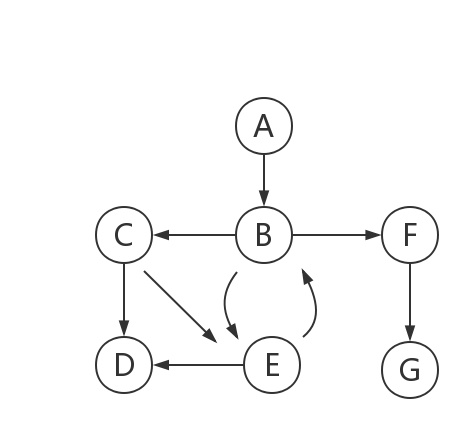
①访问A。
②依次访问C,D,F。在访问了A之后,接下来访问A的邻接点。前面已经说过,在本文实现中,顶点ABCDEFG按照顺序存储的,C在"D和F"的前面,因此,先访问C。再访问完C之后,再依次访问D,F。
③依次访问B,G。在第2步访问完C,D,F之后,再依次访问它们的邻接点。首先访问C的邻接点B,再访问F的邻接点G。
④访问E。在第3步访问完B,G之后,再依次访问它们的邻接点。只有G有邻接点E,因此访问G的邻接点E。
因此访问顺序是:A -> C -> D -> F -> B -> G -> E
又称为"宽度优先搜索"或"横向优先搜索",简称BFS。从图中某顶点v出发,在访问了v之后依次访问v的各个未曾访问过的邻接点,然后分别从这些邻接点出发依次访问它们的邻接点,并使得“先被访问的顶点的邻接点先于后被访问的顶点的邻接点被访问,直至图中所有已被访问的顶点的邻接点都被访问到。如果此时图中尚有顶点未被访问,则需要另选一个未曾被访问过的顶点作为新的起始点,重复上述过程,直至图中所有顶点都被访问到为止。换句话说,广度优先搜索遍历图的过程是以v为起点,由近至远,依次访问和v有路径相通且路径长度为1,2...的顶点。
教材学习中的问题和解决过程
- 问题1:无向图的广度优先遍历中,第一个顶点有三个邻接顶点,那么下一次遍历的时候必须从最右一个顶点开始遍历吗?
- 问题1解决方案:类似于树的遍历,在同一层中,元素的遍历都是从左到右的进行遍历,图中看似是从右边一个元素开始的,但是第一个遍历的顶点按照树的结构画出来,依旧是从左至右开始遍历。如图是一个图的遍历的顺序.
- 问题2:addEdge方法里运用到的几个方法getIndex、indexIsValid分别是什么意思
- 问题2解决方案:因为无向图的实现是由一个顶点列表和邻接矩阵组合而成的,所以如果要在两个顶点之间添加一条边,首先需要在顶点列表中找到这两个顶点,getIndex就是这样一个方法,用于定位正确的索引。indexIsValid则是用于判断索引值是否合法,如果合法的话就把邻接矩阵内两个顶点之间对应的值改为true。另一方面,顶点列表的索引值可以用于邻接矩阵,譬如顶点列表索引值为一的位置的元素也就是邻接矩阵第一行第一个或者第一列第一个表示的值。所以代码实现时在这里可以直接写
adjMatrix[index1][index2] = true, adjMartix[index2][index1] = true。
- 问题3:深度优先遍历的遍历顺序以及两种遍历的代码
- 问题3解决方案:
public Iterator iteratorBFS(T startVertex) {
return iteratorBFS(getIndex(startVertex));
}//公有方法,同样是找到起始顶点在顶点列表中的索引
private Iterator iteratorBFS(int startIndex) {
Integer x;
Queue<Integer> tq = new LinkedQueue<Integer>();
UnorderedListADT<T> rls = new ArrayUnoderedQueue<T>();//广度优先遍历需要一个队列和一个无序列表
if (!indexIsValid(startIndex)) {
return rls.iterator();
}//判断索引值是否合法,如果不合法,返回一个rls的迭代,显示出来就是空
boolean[] visited = new boolean[numVertices];
for (int i = 0; i < numVertices; i++) {
visited[i] = false;
}//创建一个存储量为图的顶点数大小的布尔值数组,将数组内每一个值都设置为false,表示未访问过
tq.enqueue(new Integer(startIndex));//将起始顶点的值存在队列中
visited[startIndex] = true;//将起始顶点对应的在布尔值数组中的位置设为true,表示已访问
while (!tq.isEmpty()) {
// 出队列
x = tq.dequeue();
// 遍历记录表
rls.addToRear(vertices[x.intValue()]);//将每一个已访问的顶点值存入无序列表中
for (int i = 0; i < numVertices; i++) {
if (adjMatrix[x.intValue()][i] && !visited[i]) {//这里可以用邻接矩阵来表示它的相邻顶点,因为如果两个顶点是连通的的话,那么adjMatrix[x.intValue()][i]将会为true,所以这里的intValue方法应该也是定位数字的索引值
tq.enqueue(new Integer(i));
visited[i] = true;
}//将与该顶点相邻且未访问过的顶点按照之前的顺序,先存入队列中,然后将其在visited中的对应位置改为true,直到队列不为空,遍历结束
}
}
return new GraphIterator(rls.iterator());v
代码调试中的问题和解决过程
- 问题一:最小生成树“mstNetwork”。
- 问题一解决方法:
public Graph nstNetwork()
{
int x, y;
int index;
int weight;
int[] edge = new int[2];
HeapADT<Double> minHeap = new LinkedHeap<Double>();
Network<T> resultGraph = new Network<T>();
if (isEmpty() || !isConnected())
return resultGraph;//当图是空的或者没有连通的时候返回一个空的引用
resultGraph.adjMatrix = new boolean[numVertices][numVertices];//创建一个邻接矩阵
for (int i = 0; i < numVertices; i++)
for (int j = 0; j < numVertices; j++)
resultGraph.adjMatrix[i][j] = Double.POSITIVE_INFINITY;
resultGraph.vertices = (T[])(new Object[numVertices]);
boolean[] visited = new boolean[numVertices];
for (int i = 0; i < numVertices; i++)
visited[i] = false; //把所有的顶点都设置为未访问过的
edge[0] = 0;
resultGraph.vertices[0] = this.vertices[0];
resultGraph.numVertices++;
visited[0] = true;
// Add all edges that are adjacent to vertex 0 to the stack.
for (int i = 0; i < numVertices; i++)
{
minHeap.addElement(new Double(adjMatrix[0][i]))
}//将所有含起始顶点的边按照权重次序添加到最小堆中
while ((resultGraph.size() < this.size()) && !minHeap.isEmpty())
{
// Pop an edge off the stack and add it to the resultGraph.
do{
weight = (minHeap.removeMin()).doubleValue();
edge = getEdgeWithWeightOf(weight, visited);
}//从堆中取出最小边
while(!indexIsValid(edge[0]) || !indexIsValid(edge[1]));
x = edge[0];
y = edge[1];
if (!visited[x])
index = x;
if (!visited[y])
index = y;
//从最小边中的两个顶点中选出未访问的一个顶点,并将索引值赋给index
resultGraph.vertices[index] = this.vertices[index];
visited[index] = true;
resultGraph.numVertices++;//将新顶点的信息赋给相应数组
resultGraph.adjMatrix[x][y] = this.adjMatrix[x][y];
resultGraph.adjMatrix[y][x] = this.adjMatrix[y][x];
// 添加所有含该新顶点且另一顶点尚不在最小生成树中的边,直到最小树中包含图中的所有顶点或者最小堆中已经没有元素
for (int i = 0; i < numVertices; i++)
{
if (!visited[i] && this.adjMatrix[i][index] < Double.POSITIVE_INFINITY)
{
edge[0] = index;
edge[1] = i;
minHeap.addElement(new Double(adjMatrix[index][i]));
}
}
}
return resultGraph;
}
- 问题2:如何解决空间不足的问题
- 问题2解决方案:可以直接引用ArrayList中的expandCapacity()
private void expandCapacity() {
T[] larger = (T[]) (new Object[tree.length * 2]);
for (int index = 0; index < tree.length; index++)
larger[index] = tree[index];
tree = larger;
}
[代码托管]https://gitee.com/besti1823/2012_327_zhao_tianhao.git


上周考试错题总结
上周无考试
结对及互评
评分标准
-
正确使用Markdown语法(加1分):
- 不使用Markdown不加分
- 有语法错误的不加分(链接打不开,表格不对,列表不正确...)
- 排版混乱的不加分
-
模板中的要素齐全(加1分)
- 缺少“教材学习中的问题和解决过程”的不加分
- 缺少“代码调试中的问题和解决过程”的不加分
- 代码托管不能打开的不加分
- 缺少“结对及互评”的不能打开的不加分
- 缺少“上周考试错题总结”的不能加分
- 缺少“进度条”的不能加分
- 缺少“参考资料”的不能加分
-
教材学习中的问题和解决过程, 一个问题加1分
-
代码调试中的问题和解决过程, 一个问题加1分
-
本周有效代码超过300分行的(加2分)
- 一周提交次数少于20次的不加分
-
其他加分:
- 周五前发博客的加1分
- 感想,体会不假大空的加1分
- 排版精美的加一分
- 进度条中记录学习时间与改进情况的加1分
- 有动手写新代码的加1分
- 课后选择题有验证的加1分
- 代码Commit Message规范的加1分
- 错题学习深入的加1分
- 点评认真,能指出博客和代码中的问题的加1分
- 结对学习情况真实可信的加1分
-
扣分:
- 有抄袭的扣至0分
- 代码作弊的扣至0分
- 迟交作业的扣至0分
点评模板:
-
博客中值得学习的或问题:
- 同学们已经有意识的遇见错误就截图,给后面写博客的各种方便很多,我一直忘记只能重新敲一遍。
-
代码中值得学习的或问题:
- 条条大路通罗马,好多同学可以曲线思维弄出代码,听他们讲解后真的很佩服。
-
基于评分标准,我给本博客打分:11分。得分情况如下:正确使用Markdown语法+1.教材学习中的问题和解决过程+2.代码调试中的问题和解决过程+2.感想,体会不假大空+1.错题学习深入+1.点评认真,能指出博客和代码中的问题+1.结对学习情况真实可信+1.课后题有验证+1,进度条有记录+1.
点评过的同学博客和代码
其他(感悟、思考等,可选)
- 每节课的考试让我十分吃不消,不只是英语单方面的问题,Java也有许多问题亟待解决,因为课本版本不同,找起知识点来比较麻烦。
- 好多同学好牛,自己好菜,各种把打好的代码推翻重来,参考别人代码改来改去把自己的程序变成了四不像,运行不了,本周更加熟悉了运行一个目的堆了四五个程序的Java常态,继续虚心学习吧。
-突然反应过来,本学期Java学习已经接近尾声,该好好思考自己学到什么了。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 5000行 | 30篇 | 400小时 | |
| 第一周 | 200/200 | 2/2 | 20/20 | |
| 第二周 | 350/500 | 2/4 | 24/38 | |
| 第三周 | 512/1000 | 3/7 | 22/60 | |
| 第四周 | 1158/1300 | 4/9 | 35/90 | |
| 第五周 | 2905/3000 | 6/5 | 24/24 | |
| 第六周 | 3927/4000 | 2/2 | 26/30 | |
| 第七周 | 9401/6000 | 3/4 | 30/50 | |
| 第八周 | 9401/7000 | 1/1 | 30/30 | |
| 第九周 | 12800 /8000 | 3/3 | 48/30 | |
| 第十周 | 14720 /10000 | 3/3 | 50/30 |




