leetcode 399. Evaluate Division(除法求值) [带权并查集]
给出方程式 A / B = k, 其中 A 和 B 均为代表字符串的变量, k 是一个浮点型数字。根据已知方程式求解问题,并返回计算结果。如果结果不存在,则返回 -1.0。
示例 :
给定 a / b = 2.0, b / c = 3.0
问题: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ?
返回 [6.0, 0.5, -1.0, 1.0, -1.0 ]
输入为: vector<pair<string, string>> equations, vector& values, vector<pair<string, string>> queries(方程式,方程式结果,问题方程式), 其中 equations.size() == values.size(),即方程式的长度与方程式结果长度相等(程式与结果一一对应),并且结果值均为正数。以上为方程式的描述。 返回vector类型。
基于上述例子,输入如下:
equations(方程式) = [ [“a”, “b”], [“b”, “c”] ],
values(方程式结果) = [2.0, 3.0],
queries(问题方程式) = [ [“a”, “c”], [“b”, “a”], [“a”, “e”], [“a”, “a”], [“x”, “x”] ].
输入总是有效的。你可以假设除法运算中不会出现除数为0的情况,且不存在任何矛盾的结果。
题解: 首先可以很容易想到,给出的关系式可以用于建图,变量名即节点,关系式结果即两变量名的权值.并且为有向边,如a / b = 2.0即 a–>b,边权为2.0,而b–>a边权为0.5.
并且这样的关系具有传递性如 a—2.0—>b—3.0—>c,那么a---->c的权值即2.0*3.0=6.0
相反,c—>a 的权值同样为1/6,即a—>c的倒数.
在这个基础上,我们可以构造一棵树,或者更准确的说是一个DAG(有向无环图),你可能会问,为什么是树不是图,并且这个关系式的构造方式明显可以形成环.
可以这样想,根据给出的关系式,已经确定了两者关系是 [前者 / 后者 = 权值] 那么在建图时就一定要建立 前者 —> 后者 ,val=权值 的边吗?答案是否定的,我们完全可以根据 原式逆向建单项边 后者 —> 前者 ,val=1/权值
如此以来建图的方式就很灵活了,这样构造出DAG是完全没问题的.
再者,我们将其抽象成一棵树,从存在相互关系的变量集合中任选一个变量作为根节点. 这样有一个好处,从根节点到达树上任意节点的结果都可以传递性预处理出来,也就是可以将路径压缩. 而树上任意两个节点A、B的关系,等于 val[root---->A] / val[root---->B] 或 val[root---->B] / val[root---->A]
存储方式不需要直接建图,而是用并查集实现,并且可以实现路径压缩,将每个集合所有节点的val压缩成与根节点的val.
拿代码中的并查集方式来举例子.
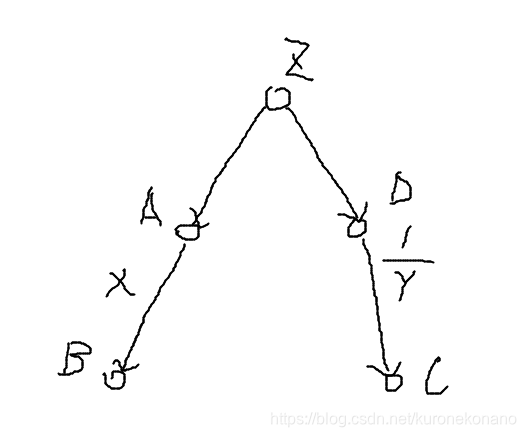
首先将变量名映射为整型节点,默认值较小的节点为父节点.
假设D的序号相对C更小,作为C的父节点
给出关系 A / B = X , C / D = Y
那么val[B] = A / B =X , val[C] = D / C = 1 / Y
当要求值 B / C 时, 实际上是 (B / Z) * (Z / C)
假设我们已经获取了路径压缩的值 val[B] = Z / B , val[C] = Z / C
最终的结果即 B / C = val[C] / val[B]
在输入关系时进行路径压缩,并计算压缩后的权值.
最后遍历查询,直接判断是否有解,有解即用val中压缩好的权值相除即可
class Solution {
public:
vector<int>fa;
vector<double>val;
int finds(int z)//并查集查询并路径压缩
{
if(fa[z]==z)
{
return z;
}
else
{
int tmp=fa[z];
fa[z]=finds(fa[z]);
val[z]*=val[tmp];
return fa[z];
}
}
vector<double> calcEquation(vector<vector<string>>& equations, vector<double>& values, vector<vector<string>>& queries) {
map<string,int>m;
m.clear();
fa.clear();
val.clear();
int num=0;
vector<double>ans;
val.push_back(0);
fa.push_back(0);
for(int i=0;i<equations.size();i++)
{
string a=equations[i][0];
string b=equations[i][1];
if(m[a]==0)
{
m[a]=++num;
fa.push_back(num);
val.push_back(1);
}
if(m[b]==0)
{
m[b]=++num;
fa.push_back(num);
val.push_back(1);
}
if(m[a]<m[b])
{
val[m[b]]=values[i];
fa[m[b]]=m[a];
fa[m[b]]=finds(m[b]);//路径压缩
}
else
{
val[m[a]]=1.0/values[i];//反边
fa[m[a]]=m[b];
fa[m[a]]=finds(m[a]);//路径压缩
}
}
for(int i=0;i<queries.size();i++)
{
string a=queries[i][0];
string b=queries[i][1];
if(m[a]==0||m[b]==0)//未出现在关系式中底变量,直接无解
{
ans.push_back(-1.0);
continue;
}
fa[m[a]]=finds(m[a]);
fa[m[b]]=finds(m[b]);
if(fa[m[a]]!=fa[m[b]])//不在同一个集合中的变量,没有任何关系,无解
{
ans.push_back(-1.0);
continue;
}
double aa=val[m[a]];
double bb=val[m[b]];
ans.push_back(bb/aa);
}
return ans;
}
};


