19. 平衡二叉树

一、什么是平衡二叉树

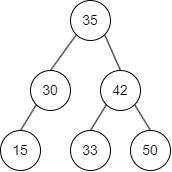
  平衡二叉树（Balanced Binary Tree，简称 AVL 树）是带有平衡条件的二叉搜索树。它可以是空树，如果不空，它的任一结点的左、右子树高度差的绝对值不超过 1，即 平衡因子（Balance Factor，简称 BF）的绝对值 \(|BF(T)| = h_{L} - h_{H} ≤ 1\)。

typedef int ElementType;

typedef struct TreeNode
{
    ElementType Data;
    struct TreeNode * Left;
    struct TreeNode * Right;
} TreeNode, * BalancedBinaryTree, * Position;

二、获取树的高度

/**
 * @brief 获取树的高度
 * 
 * @param T 平衡二叉树
 * @return int 树的高度
 */
int Height(BalancedBinaryTree T)
{
    if (T == NULL)
    {
        return 0;
    }
  
    int LeftHeight = Height(T->Left);
    int RightHeight = Height(T->Right);

    return ((LeftHeight > RightHeight) ? LeftHeight : RightHeight) + 1;
}

三、平衡二叉树的调整

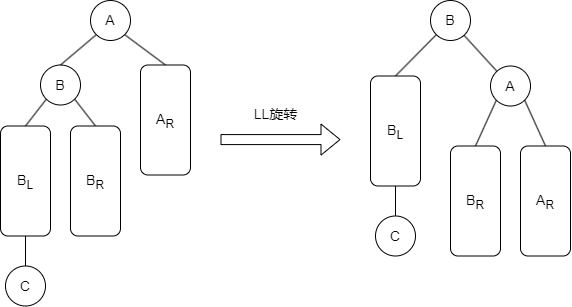
3.1、LL旋转

  LL 平衡旋转（右单旋转）。由于在结点 A 的左孩子（L）的左子树（L）上插入新结点，导致 A 的平衡因子有 1 增至 2，导致以 A 为根的子树失去平衡，需要一次向右的旋转操作。将 A 的左孩子 B 向右上旋转代替 A 成为根结点，将 A 结点向右下旋转成为 B 的右子树的根结点，而 B 的原右子树则作为 A 结点的左子树。

/**
 * @brief LL旋转
 * 
 * @param A 要旋转的结点的根结点
 * @return Position 旋转后的根结点
 */
Position SingleRotateWithLeft(Position A)
{
    Position B = A->Left;                                                       // 结点B为结点A的左孩子
    A->Left = B->Right;                                                         // 结点A的左孩子指向结点B的右孩子
    B->Right = A;                                                               // 结点B的右孩子指向结点A

    return B;
}

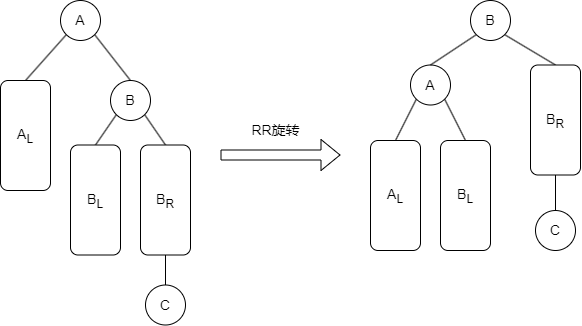
3.2、RR旋转

  RR 平衡旋转（左单旋转）。由于在结点 A 的右孩子（R）的右子树（R）上插入新结点，导致 A 的平衡因子有 -1 减至 -2，导致以 A 为根的子树失去平衡，需要一次向左的旋转操作。将 A 的右孩子 B 向左上旋转代替 A 成为根结点，将 A 结点向左下旋转成为 B 的左子树的根结点，而 B 的原左子树则作为 A 结点的右子树。

/**
 * @brief RR旋转
 * 
 * @param A 要旋转结点的根结点
 * @return Position 旋转后的根结点
 */
Position SingleRotateWithRight(Position A)
{
    Position B = A->Right;                                                      // 结点B为结点A的右孩子
    A->Right = B->Left;                                                         // 结点A的右孩子指向结点B的左孩子
    B->Left = A;                                                                // 结点B的左孩子指向结点A

    return B;
}

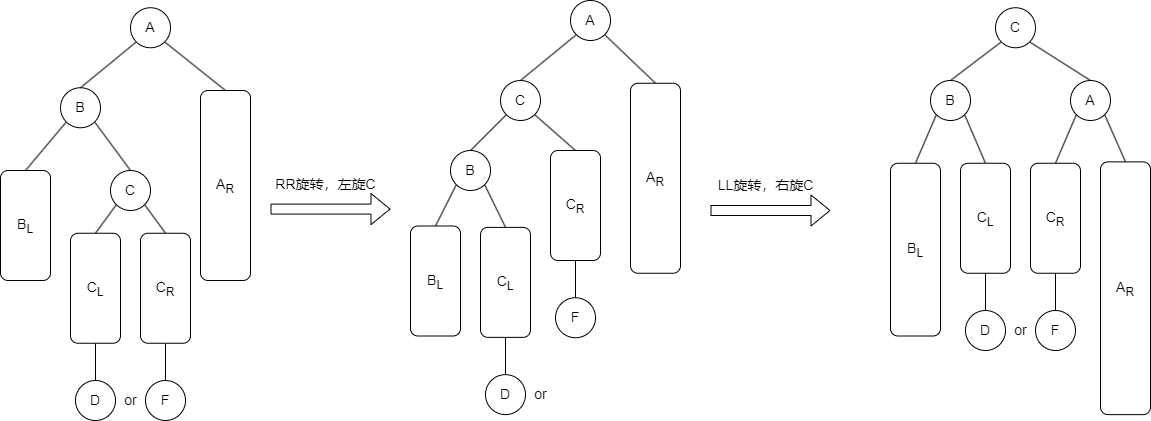
3.3、LR旋转

  LR 平衡旋转（先左后右双旋转）。由于在结点 A 的左孩子（L）的右子树（R）上插入新结点，导致 A 的平衡因子有 1 增至 2，导致以 A 为根的子树失去平衡，需要进行两次旋转操作，先左旋转后右旋转。将 A 的左孩子 B 的右子树的根结点 C 向左上旋转提升到 B 结点的位置，然后再把该 C 结点向右上旋转提升到 A 结点的位置。

/**
 * @brief LR旋转
 * 
 * @param A 要旋转结点的根结点
 * @return Position 旋转后的根结点
 */
Position DoubleRotateWithLeft(Position A)
{
    A->Left = SingleRotateWithRight(A->Left);                                  // 先对A的左子树进行一次RR旋转
    return SingleRotateWithLeft(A);                                             // 再对A进行一次LL旋转
}

3.4、RL旋转

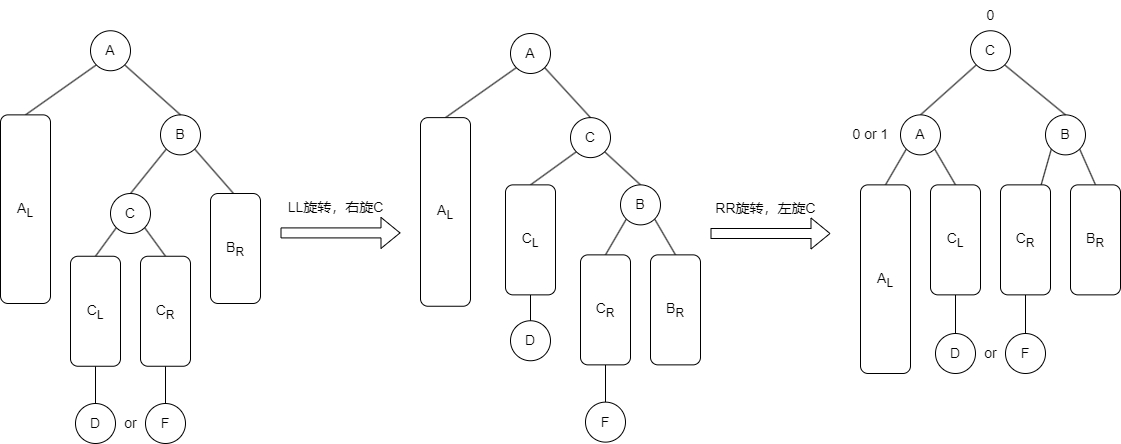
  RL 平衡旋转（先右后左双旋转）。由于在结点 A 的右孩子（R）的左子树（L）上插入新结点，导致 A 的平衡因子有 -1 减至 -2，导致以 A 为根的子树失去平衡，需要进行两次旋转操作，先右旋转后左旋转。将 A 的右孩子 B 的左子树的根结点 C 向右上旋转提升到 B 结点的位置，然后再把该 C 结点向左上旋转提升到 A 结点的位置。

/**
 * @brief RL旋转
 * 
 * @param A 要旋转结点的根结点
 * @return Position 旋转后的根结点
 */
Position DoubleRotateWithRight(Position A)
{
    A->Right = SingleRotateWithLeft(A->Right);                                  // 先对A的右子树进行一次LL旋转
    return SingleRotateWithRight(A);                                           // 再对A进行一次RR旋转
}

三、平衡二叉树的自动调节

/**
 * @brief 失衡结点自动调节
 * 
 * @param Node 要调节的结点
 * @return Position 如果有旋转，返回旋转后的根结点，否则返回原根结点
 */
Position Balance(Position Node)
{
    if (Node == NULL)
    {
        return NULL;
    }
  
    int bf = (Height(Node->Left) - Height(Node->Right));

    if (bf > 1)
    {
        // 如果左孩子结点的左子树更高或左右子树相等，需要LL旋转，否则需要LR旋转
        if (Height(Node->Left->Left) >= Height(Node->Left->Right))         
        {
            return SingleRotateWithLeft(Node);
        }
        else
        {
            return DoubleRotateWithLeft(Node);
        }
    }
    else if (bf < -1)
    {
        // 如果右孩子结点的右子树更高左右子树相等，需要RR旋转，否则需要RL旋转
        if (Height(Node->Right->Left) <= Height(Node->Right->Right))         
        {
            return SingleRotateWithRight(Node);
        }
        else
        {
            return DoubleRotateWithRight(Node);
        }
    }
  
    return Node;
}

四、插入元素

/**
 * @brief 插入元素
 * 
 * @param T 二叉搜索树
 * @param X 要插入的元素
 * @return BalancedBinaryTree 指向二叉搜索树的指针
 */
BalancedBinaryTree Insert(BalancedBinaryTree T, ElementType X)
{
    if (T == NULL)
    {
        T = (BalancedBinaryTree)malloc(sizeof(TreeNode));
        T->Data = X;
        T->Left = T->Right = NULL;
    }
    else
    {
        if (X < T->Data)
        {
            T->Left = Insert(T->Left, X);                                       // 左子树递归插入
        
        }
        else if (X > T->Data)
        {
            T->Right = Insert(T->Right, X);                                     // 右子树递归插入
        }
        else
        {
            T->Data = X;                                                        // 找到则更新元素
        }
    }

    return Balance(T);
}

五、删除元素

/**
 * @brief 删除元素
 * 
 * @param T 平衡二叉树
 * @param X 要删除的元素
 * @return BalancedBinaryTree 指向平衡二叉树的指针
 */
BalancedBinaryTree Delete(BalancedBinaryTree T, ElementType X)
{
    Position P = NULL;

    if (T == NULL)
    {
        return NULL;
    }

    if (X < T->Data)
    {
        T->Left = Delete(T->Left, X);                                           // 左子树递归删除
    }
    else if (X > T->Data)
    {
        T->Right = Delete(T->Right, X);                                         // 右子树递归删除
    }
    else
    {
        if (T->Left && T->Right)                                                // 被删除的结点存在左右子树
        {
            P = FindMax(T->Left);                                               // 找到左子树最大值
            T->Data = P->Data;                                                  // 删除右子树最小值
            T->Left = Delete(T->Left, T->Data);                                 // 删除左子树最大值
        }
        else                                                                    // 被删除结点没有子结点或者只有一个子树
        {
            P = T;
            if (T->Left == NULL)                                                // 有右孩子或者无子结点
            {
                T = T->Right;
            }
            else if (T->Right == NULL)                                          // 有左孩子或者无子结点
            {
                T = T->Left;
            }

            free(P);
        }
    }

    return Balance(T);
}