2.1经验误差与过拟合
错误率 = a个样本分类错误/m个样本
精度 = 1 - 错误率
误差：学习器实际预测输出与样本的真是输出之间的差异。
训练误差：即经验误差。学习器在训练集上的误差。
泛化误差：学习器在新样本上的误差。
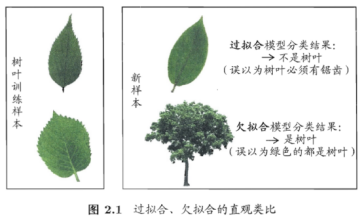
过拟合：学习器把训练样本学的”太好”，把不太一般的特性学到了，泛化能力下降，对新样本的判别能力差。必然存在，无法彻底避免，只能够减小过拟合风险。
欠拟合：对训练样本的一半性质尚未学好。
2.2评估方法
(在现实任务中，还需考虑时间、存储空间等开销，和其他因此。这里只考虑泛化误差。)
用一个测试集来测试学习其对新样本的判别能力，然后以测试集上的测试误差作为泛化误差的近似。
在只有一个包含m个样例的数据集D，从中产生训练集S和测试集T。
2.2.1留出法
D分为两个互斥的集合，一个作为S，一个作为T。
分层采样：S和T中正例和反例比例一样。
例如D包含500个正例，500反例。分层采样获得含70%样本的S，有350正例，350反例；30%样本的T，有150正例，150反例。
一般采用随机划分、重复进行实验评估后取平均值作为留出法的评估结果。
例如，进行100次随机划分，每次产生一个训练/测试集用于实验评估，100次后得到100个结果，而留出法返回的则是这100个结果的平均。
弊端：T比较小，评估结果不够稳定准确，偏差大。
常见将大约2/3~4/5的样本用于训练，剩余样本用于测试。
2.2.2交叉验证法
将D划分为k个大小相似的互斥子集。(D通过分层采样得到每个子集Di,保持数据分布一致性)。每次用k-1个子集的并集作为训练集，余下那个作测试集。即可获得K组训练/测试集，进行K次训练和测试，最终返回k个测试结果的均值。也称”k折交叉验证”。
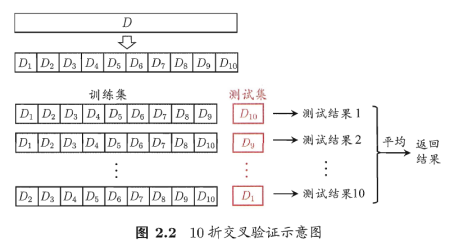
为减小因样本划分不同而引入的差别，k折交叉验证要随机使用不同的划分重复p次，最终评估结果是这p次k折交叉验证结果的均值，即进行p*k次训练/测试。
留一法：m个样本划分成m个子集，每个子集包含一个样本。留一法中被实际评估的模型与期望评估的用D训练出来的模型很相似，因此，留一法的评估结果往往被认为比较准确。
留一法缺陷：数据集较大，例如，数据集包含100w个样本，则需训练100w个模型。且留一法的估计结果未必比其他评估法准确。
2.2.3自助法
从m个样本的数据集D，随机采样(选)一个样本，拷贝入训练D’，放回，继续随机挑选，直至m次。
样本在m次采样中始终不被踩到的概率(1-1/m)^m。
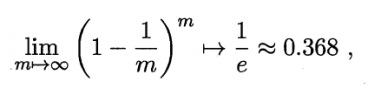
实际评估的模型与期望评估的模型都使用m个训练样本，而仍有约1/3的没有在训练集的样本用于测试。
自助法在数据集较小、难以有效划分训练/测试集时很有用。在初始数据量足够时，留出法和交叉验证法更常用。
2.2.4调参与最终模型
①选择适合的学习算法
②对算法参数进行设定，调参
2.3性能度量
性能度量：衡量模型泛化能力的评价标准。
给定样例集D={(x1,y1),(x2,y2),……,(xm,ym)},yi是对xi的真实标记，要评估学习器f的性能，就要把学习器预测结果f(x)与真实标记y进行比较。
均方误差：
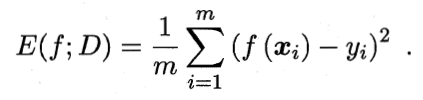
数据分布D和概率密度函数p(.),均方误差：
2.3.1错误率与精度
错误率：分类错误的样本数占样本总数的比例。
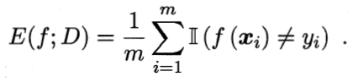
精度：分类正确的样本数占样本总数的比例。
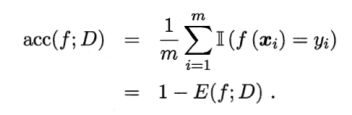
数据分布D和概率密度函数p(.)。
错误率：
精度：
2.3.2查准率、查全率与F1
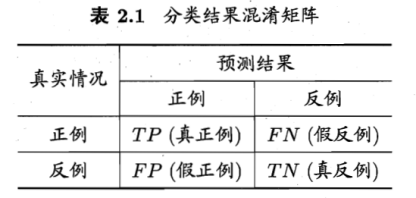
二分类
True positive 真正例
False positive 假正例
True negative 真反例
False negative 假反例
TP+FP+TN+FN = 样例总数
①查准率P
查全率R
通常，查准率高时，查全率偏低；查全率高时，查准率偏低。
例如，若希望好瓜尽可能的挑选出来，则可通过增加选瓜的数量来实现，查准率就会低；
若希望挑出的瓜中好瓜比例尽可能高，则可挑选有把握的瓜，必然会漏掉好瓜，查全率就低了。
学习器把最可能是正例的样本排在前面。按此排序，把样本作为正例进行预测，根据PR绘图。
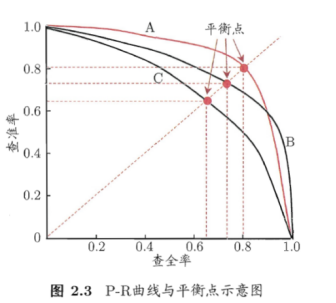
如果一个学习器的PR曲线包住了另一个，则可以认为A的性能优于C。
如果有交叉，如A、B，期望PR双高，综合考虑PR性能。
引入平衡点(BEP)，基于BEP比较，A优于B。
②更常用的是F1度量：
Fβ ：F1的一般形式，能让我们表达对查准率/查全率的不同偏好。
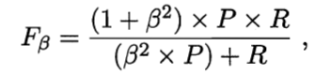
Β>0度量了查全率对查准率的相对重要性；β=1退化为F1；β>1查全率有更大影响；β<1查准率有更大影响。
③在混淆矩阵上分别计算查准率和查全率，在计算平均值，得到宏查准率，宏查全率，以及宏F1。
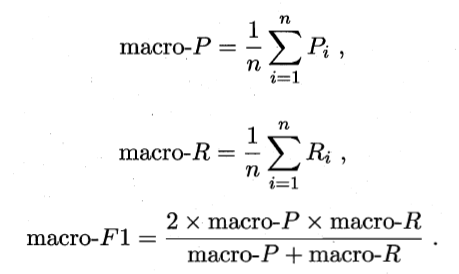
④将各混淆矩阵的对应元素进行平均，得到TP、FP、TN、FN的平均值，记为
，在计算出微查准率，微查全率，以及微F1。
2.3.3 ROC AUC
最可能是正例的样本排在前面，按此排序。排序中某个截断点，前一部分判断正例，后一部分为反例。不同任务中根据需求划分截断点；重视查准率，靠前位置截断；重视查全率，靠后位置截断。
ROC：纵轴：真正例率TPR；横轴：假正例率FPR
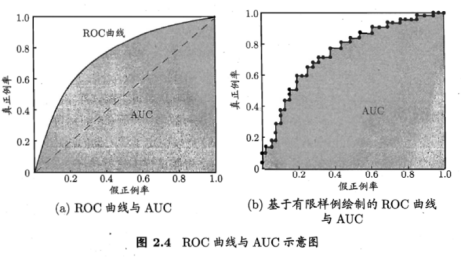
现实中，有限个测试样例绘制ROC，不可能光滑。只能像右图一样。
前一个标记点坐标为(x,y)，当前若为真正例，则标记为；假正例，用线段连接。
若一个学习器的ROC曲线被另一个包住，后者的性能能优于前者；若交叉，判断ROC曲线下的面积，即AUC。
AUC考虑的是样本预测的排序质量，因此它与排序误差有紧密联系。给定m+个正例，m-个反例，令D+和D-分别表示正、反例集合，则排序”损失”定义为
Lrank对应ROC曲线之上的面积：若一个正例在ROC曲线上标记为(x,y)，则x恰是排序在期前的所有反例所占比例，即假正例，因此：
2.3.4代价敏感错误率与代价曲线
代价矩阵：
costij表示将第i类样本预测为第j类样本的代价。
非均等代价下，希望总体代价最小化。
若假设第0类为正类，1为反类。D+代表例集正例子集，D-反例子集，则代价敏感错误率为：
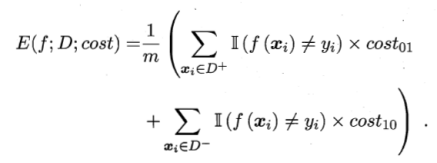
在非均等代价下，ROC不能直接反应出学习器的期望总体代价，代价曲线可以。横轴为[0,1]的正例函数代价
p是样例为正例的概率；纵轴是取值为[0,1]的归一化代价
FPR假正例率，FNR=1-TPR假反例率。
ROC每个点，对应代价平面上一条线。
例如，ROC上(TPR,FPR),计算出FNR=1-TPR，在代价平面上绘制一条从(0,FPR)到(1,FNR)的线段，面积则为该条件下期望的总体代价。所有线段下界面积，所有条件下学习器的期望总体代价。
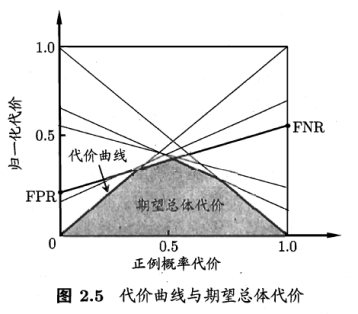
按照图来看，最终总体代价越来越小。(学习器，不断进步！)
2.4比较检验
默认以错误率为性能度量，用ε表示。
2.4.1假设检验
学习器泛化错误率，并不能测量；只能获知其测试错误率
。泛化错误与测试错误率未必相同，但两者接近的可能性比较大，因此，用后者估推出泛化错误率的分布。
泛化错误为
的学习器在一个样本上犯错的概率是
；测试错误率
意味着在m个测试样本中恰有
*m个被误分类。
包含m个样本的测试集上，泛化错误率为的学习器被测得测试错误率为的概率：
即为
给定测试错误率，则解
可知，
在
时最大，
增大时
减小。符合二项分布。
例如，=0.3，则10个样本中3个被误分类的概率最大。
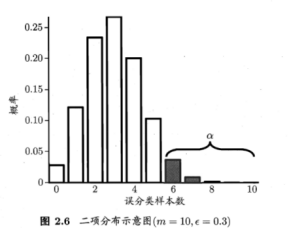
①我们根据图表粗略估计ε0，比如这幅图当中ε0可取5,6,7都可以，然后求出总体概率α，我们把大多数样本分布的区间1-α称为置信区间，所以只要不超过ε0，即在置信度下就是符合条件的假设 ，否则被抛弃，即在α显著度下。
②t检验
多次重复留出法或是交叉验证法等进行多次训练/测试，得到多个测试错误率。
平均测试错误率μ和方差σ²为
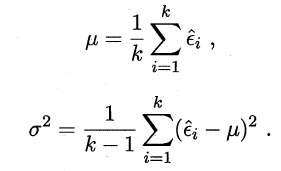
考虑到这k个测试错误率可看作泛化错误率
的独立采样，则变量
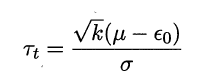
服从自由度为k-1的t分布。
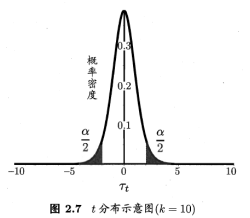
当测试错误率均值为时，在1-α概率内观测到最大的错误率，即临界值。
双边假设，阴影部分各有α/2的面积；阴影部分范围为
和
。
若平均错误率μ与之差|μ-|位于临界值
范围内，则可认为泛化错误率为，置信度为1-α；否则，认为在该显著度下可认为泛化错误率与有显著不同。
2.4.2 交叉验证t检验
对不同学习器的性能进行比较。
两个学习器A、B,若使用k折交叉验证法得到的测试错误率分别为
，其中
是在相同的第i折训练/测试集上得到的结果，可用k折交叉验证”成对t检验”来进行比较检验。
，使用相同的训练/测试集的测试错误率相同，两个学习器性能相同。
k折交叉验证产生k对测试错误率：对没对结果求差
；若性能相同则是0。用
，t检验，计算差值的均值μ和方差σ²。
若变量
小于临界值
，则认为两个学习器的性能没有显著差别；否则，可认为两个学习器性能有显著差别，错误平均率小的那个学习器性能较优。
5*2交叉验证
假设检验的前提：测试错误率均为泛化错误率的独立采样。
因样本有限，加查验证不同轮次训练集有重叠，测试错误率实际上不独立，会导致过高估计假设成立的概率。5*2交叉验证，可缓解这一问题。
5*2交叉验证，5次2折交叉验证。A、B第i次2折交叉验证产生两对测试错误率，对它们分别求差，得到第1折上的差值
和第2折上的差值
。为缓解测试错误率的非独立性，仅计算第一次2折交叉验证的结果平均值
。
对每次结果都计算出方差
变量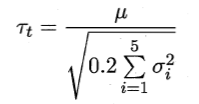
服从自由度为5的t分布，其双边检验的临界值
。
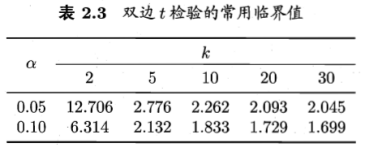
当α=0.05时为2.5706；α=0.1是为2.0150。
2.4.3 McNemar检验
列联表：估计学习器A、B的测试错误率；获得两学习分类结果的差别，两者都正确，都错误或者一个正确一个错。
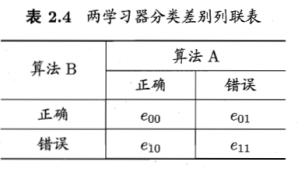
若假设A、B学习器起能相同，则应由e01=e10，那么|e01-e10|应服从正态分布。McNemar检验考虑变量
，服从自由度为1的
分布，即标准正态分布变量的平方。给定显著度α，当以上变量值小于临界值
时，认为两学习器性能没有显著差别；否则性能又显著差别。当α=0.05时为3.8415；α=0.1是为2.7055.
2.4.4 Friedman检验与 Nemenyi后续检验
①一组数据集上对多个算法进行比较，基于算法排序的Friedman检验。
假定用D1、D2、D3、D4四个数据集对ABC进行比较，由好到怀排序，并赋予序值1,2，……
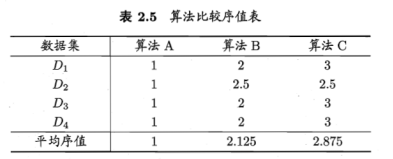
性能相同，平均序值应当相同。
假定N个数据集上比较k个算法，令ri表示第i个算法的平均序值。简化考虑不考虑平分均值的情况，则ri的平均值和方差分别为。
变量
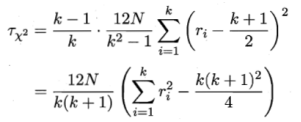在k和N都较大时，服从自由度为k-1的分布。
上述为原始Friedman检验，过于保守，现在通常使用变量
。
其中
由原式得到
。服从自由度为k-1和(k-1)(N-1)的F分布。
若”所有算法的性能相同”这个假设被拒绝，说明算法的性能显著不同。
②Nemenyi后续检验
进行”后续检验”来进一步区分个算法，常用的有 Nemenyi后续检验。
Nemenyi检验计算出平均序值差别的临界值域
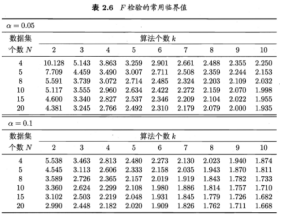
下表给出α=0.05和0.1时常用的qα值，若两个算法的平均序值之差超出了临界值域CD，则以相应的置信度拒绝”两个算法性能相同”这一假设。
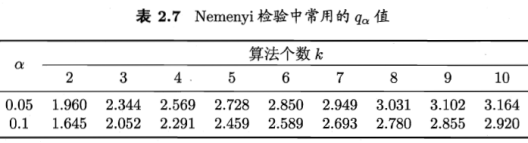
若大于α=0.05时的F检验临界值5.143，因此拒绝”所有算法性能相同”这个假设；用Nemenyi后续检验，选择k的q，根据式算出CD，可知算法两两之间是否有显著差别。
根据上面表2.5绘制出Friedman检验图。
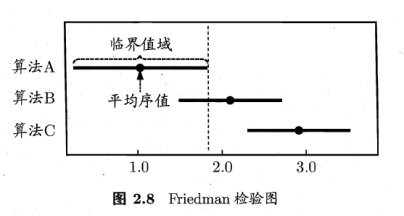
横轴：平均序列，每个算法用原点表示平均序列，横线表示临界值域大小。从图中观察，若两算法横线段有交叠，说明没有显著差别。例如图中，算法A和B没有显著差别，而算法A优于算法C，无交叠区。
2.5偏差与方差
偏差-方差分解：解释学习算法泛化性能的一种重要工具。
①偏差
对测试样本x，令yD为x在数据集中的标记，y为x的真实标记，f(x;D)为训练集D上学得模型f在x上的预测输出。
以回归任务为例，学习算法的期望预测为
使用样本数相同的不同训练集产生的方差为
噪声为
期望输出与真是标记的差别成为偏差(bias)，即
。
假定噪声期望为0，通过简单的多项式展开合并，可对算法的期望泛化误差进行分解：
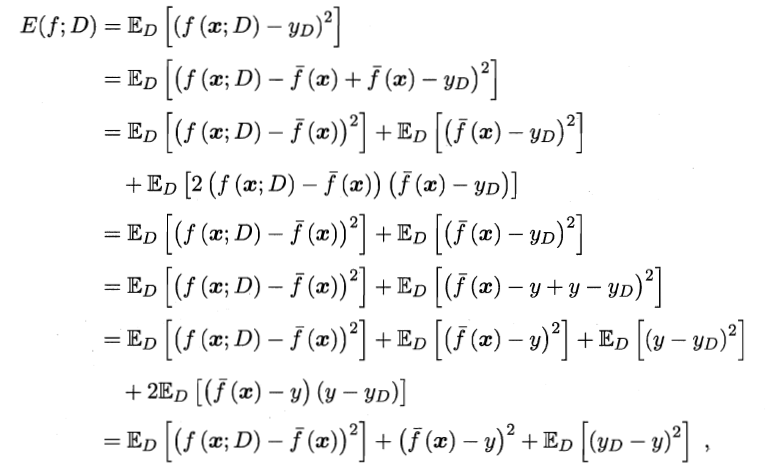
即泛化误差可分解为偏差、方差与噪声之和。
范围性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。
②方差
偏差和方差是有冲突的。
训练不足时，由偏差主导泛化误差；训练充足时，有方差主导泛化误差。
